期望时间下的移动机器人目标搜索路径规划

汪 琴 ,张波涛 ,宋士吉

(1.杭州电子科技大学自动化学院,浙江杭州 310018; 2.清华大学自动化系,北京 100084)

1 引言

移动机器人目标搜索通常是指采用一个或多个机器人对工作环境中的单个或多个目标进行信息采集或操作,属于机器人领域的重要共性技术之一,被广泛用于家庭服务、地震/火灾搜救、工业故障检测、深海/外太空环境探索等[1–2].移动机器人目标搜索涉及运动规划、机器视觉、运动控制、SLAM(simultaneous localization and mapping)等多个领域,其中,路径规划是其进行任务决策、完成复杂工作的前提[3].移动机器人的目标搜索路径规划属于全局路径规划中的任务规划,其主要目的是按照任务需求生成一条最优或次优的可行路径[3–4].

虽然多机器人协作搜索具有更高的效率,但受运输能力、成本所限,现实应用中大多采用单体机器人搜索[5–6].目前一些研究者提出了采用最短距离为指标生成搜索路径进行时间优化的方法[7],这些方法可以求解出近似最优路径.其后,研究者发现最短距离为目标的搜索方式忽视了任务中的不确定性因素,假设目标呈均匀分布,搜索距离与时间呈现非线性关系.然而,该假设在实际应用中难以成立.为解决此问题,Sarmiento等在搜索中引入了概率方法[5],考虑了环境中的不确定性因素,使运动规划更贴近实际,同时也意味着评价标准会因任务需求不同而多样化,可为期望时间、最短距离、待遍历节点数等.为了更适应于实际环境需求,Espinoza等在文献[5]的工作基础上,将搜索环境由2D拓展至3D,将移动机械臂的手眼引入概率目标搜索,用手眼拓展机器人的搜索能力,减少了本体移动,从而优化期望搜索时间[8].文献[9]提出了以最大可靠性为指标的目标搜索方法,并分析了文献[5]所提出的“搜索分布概率是确定的,且搜索过程中移动机器人的速度是恒值”假设的局限性.近年来国内外一些研究者尝试将搜索模式进行细化研究,但截至目前只分析了有限的几种模式,如最短距离搜索、最优期望时间搜索、最大可靠性搜索等[7].以期望时间为指标的路径规划综合考虑了目标分布的不确定性和需求指标的多样性,比采用单一的最短时间、最短距离为指标的规划方法更能适应不同的搜索环境.

对于以最优期望时间为指标的移动机器人目标搜索,文献[6]通过在机器人目标搜索问题中引入概率指标,使机器人搜索问题的理论模型与人类寻找物体的策略更相近,该方法的不足之处在于假设物体在工作环境下服从均匀分布,且正比于可行域面积,这种假设过于理想化[5,8],与实际工作环境相悖,从而导致该方法的表现虽比基于确定性指标的方法要好,但理论概率分布模型与实际的误差会降低搜索效率.在机器人实际工作环境中,因目标物体属性不同,出现在不同区域的概率也不同,例如:对于家庭服务机器人而言,水杯出现在餐厅的概率远高于出现在厕所的概率,电视遥控器出现在电视附近的概率远高于其它区域,目标并不呈均匀分布.针对该问题,本文设计了非均匀分布的概率测算模型,并加入了因时间变化而更新的策略.对于目标搜集、火灾救援等的搜索任务通常要求机器人搜得物体后返回出发点,但目前的最优期望时间搜索方法局限于只对获得目标前的时间进行优化,并未计入机器人携带目标返回的时间[5,10].本文对期望时间进行了全局优化,并采用多项式复杂度的改进改良圈算法替代了文献[10]中的次优贪心算法,得到全局效果较好的期望观测点序列.对于局部路径规划采用随机生成树(rapid-exploration random tree,RRT)算法,该方法适合解决高维复杂环境问题,其缺点为随机树的扩展不确定性强,易陷入局部极小值.为解决该问题,本文引入目标偏好、碰撞检测机制和非完整约束对经典RRT进行改进.

本文通过以下4部分对所提方法进行分析:首先,对目标搜索的概率测算模型进行理论分析;其后,构建上层序列规划获得期望观测点序列,并构建了下层节点间的局部路径规划;最后,通过实验测试所提算法的全局优化能力,并对结果进行分析与总结.

2 基于期望时间的多目标搜索问题

目前,移动机器人目标搜索主要方法可分为:连续方法与离散方法.前者与人类在环境中搜索物体的方式类似,但存在严重的感知区域交叉问题,难以进行全局优化;后者假设机器人按一定的顺序访问若干节点,整个规划过程被分为若干观测子阶段.在离散方法中,若搜索物体的方式亦为离散,则会延迟目标被发现的时间,降低目标被发现的概率.鉴于以上问题,一些研究者对离散方法进行改进,采取折中的方式,即:用离散规划优化节点序列,采用全景摄像机连续扫描环境[5].基于该策略,以期望时间为指标的多目标搜索问题定义如下:

定义1对于移动机器人的工作空间S,Yk(Xk)是观测点Xk对应的可视区域,该区域满足

观测点集服从

其中:X为观测点集,观测点Xk∈X.基于期望时间的搜索路径规划是在S中生成满足遍历所有观测点并返回起点的期望时间最优序列.

在实际工作环境中,目标的属性不同,出现在不同区域的概率也不同,例如:电饭煲出现在客厅的概率远低于出现在厨房的概率,针对目标在工作环境中分布不均匀的问题,本文引入了概率密度因子,以Yk(λk,Xk)表示观测点Xk对应的可见区域,该区域中目标呈非均匀分布,其中λk是Yk(λk,Xk)的密度因子,该密度因子和物体存在于区域Yk(λk,Xk)的单位面积的概率呈正相关关系,具体如下:

其中: n表示观测点的数量,pk为目标在观测点Xk所覆盖区域存在的概率.

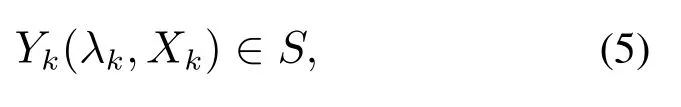
且

随着时间推移,目标在各个观测点的分布概率会发生改变,故需对各观测点的概率进行更新,采用统计方法来提高测算模型与实际环境的匹配度.

基于离散搜索理论[5],在一个工作空间S中,机器人搜索目标物体属离散事件,其概率分布如下:

搜索到目标物体的期望时间为

其中:tk表示机器人从第k个观测点到第k+1个观测点所消耗的时间,例如t1表示从第1个观测点到第2个观测点所消耗的时间;pk表示机器人在第k+1个观测点的概率,假设累计分布函数为f(T),则

其中累计分布函数如图1所示.

图1 累计分布函数Fig.1 The cumulative distribution function

3 基于优化改良圈的上层序列规划算法

拓扑序列规划目的是在特定的搜索环境下,依据某种评价标准生成任务所需的观测点序列.文献[11]用贪心算法搜索拓扑地图,其计算复杂度较低,可确保找到可行解,但所用启发式方法难以得到全局最优解.原始的改良圈算法为图论中的拓扑图搜索算法,但只能从局部进行优化,后来有研究者从全局角度考虑对改良圈算法进行改进,从而得到了一种基于优化改良圈的拓扑序列搜索算法.与文献[11]中的贪心算法相比,该方法具有更强的全局优化能力且常被用于图搜索,但并未用于概率目标搜索问题.该算法所面向的图论问题与机器人多目标搜索问题较相似,本文根据任务需求对其改进,基于该方法解决非均匀分布目标的搜索问题.面向多目标搜索问题的改良圈搜索机制如下:若目标在S中满足非均匀分布,则遍历全部观测点,并返回起始点,移动机器人所走过的路径记为L,根据权值最小原则反复修正L,从而得到满足期望时间最优的一条路径L1,具体步骤如下:

步骤1在工作环境S中选择一个观测点X1作为起点,寻找一条与观测点X1关联,且权值最小的边m1,m1另一端的观测点记为X2,从而得到一个观测点序列X1,X2.

步骤2观测点X2作为起点,寻找一条与观测点X2关联,权值最小的边m2,m2另一端的观测点记为X3,从而得到一个观测点序列X1,X2,X3.同理可得一个观测点序列,记为X1,X2,X3,···,Xk.

步骤3假设已选出的路径观测点访问顺序是X1,X2,X3,···,Xk,在剩下路径的观测点中找到一个与观测点Xk的权值最小的观测点,记为Xk+1.从而得到边序列:m1,m2,m3,···,mk+1.

步骤4令kk+1,重复步骤3,直至k+1n −1,得到路径L,

步骤5记路径L为改良圈算法的初始圈,当

其中:M(G)表示边的集合,w(XkXj)表示观测点Xk,Xj间的权值,L1表示新的观测点序列.

步骤6令LL1,返回步骤5,循环(n −1)!−1次.

步骤7找出回路最小权值和对应的L1,即为优化后的观测点访问顺序.

4 基于GBC–RRT的下层点对点规划

序列规划是拓扑图下生成的观测点序列,并未考虑局部环境,需要用下层P–P(point to point)规划方法根据局部环境生成一条机器人更易于跟踪的路径.目标搜索问题的局部规划问题已有大量相关研究,如:文献[5]针对凸多边形障碍以可视图法进行规划,文献[10]采用人工势场法(artifical potential field,APF)执行P–P规划,该方法的缺陷是易于陷入局部极小.RRT路径规划方法以“树”的形式在空间扩展,从而生成可行路径.它以初始点作为根节点,通过随机采样增加叶子节点的方式,生成随机扩展树,当随机树中的叶子节点包含了目标点或进入了目标区域,便可以在随机树中找到一条从初始点到目标点的路径.由于RRT算法的随机性强,导致路径的权值较大,为解决该问题,研究者对RRT方法不断改进,相继提出目标偏好RRT、双向RRT等.为克服RRT方法随机性强导致的目的趋向慢、易陷入局部极小的缺点[12–14],本文引入目标偏好和物体碰撞检测机制,对原始RRT方法加以改进,考虑全局环境信息,减小扩展的随机性、避免陷入局部极小值的问题,缩短了算法的运行时间,从而提高整体的寻优效率[15].

为克服RRT随机性强的缺陷,本文借鉴目标偏好RRT算法的策略,即设定一个阈值ρa,随机触发因子大于阈值ρa,便随机选取地图上的一个点作为下一节点的扩展方向,反之,把目标区域点当作随机目标点.此时随机搜索树从起点开始扩展,以终点为目标,从而规划出一条路径.

为避免陷入局部极小值,引入物体碰撞检测机制,碰撞检测示意图如图2所示,把Qinit当作初始状态的母节点,其子节点按图2中所示逐层向外扩展,用g表示节点在其子节点方向上的碰撞概率,节点扩展方向由g值决定.假设起始节点和目标节点间结点数为n,每个新节点的各子方向初始化为未扩展状态,且每个新节点的g值为0. Qnearest节点为最临近节点,其各子方向初始化为扩展状态,Qnearest节点的g值将会增加1/n.依次类推,假设Qinit节点是Qnearest节点的第m−1阶母节点,则Qinit节点的g值相应增加1/nm.

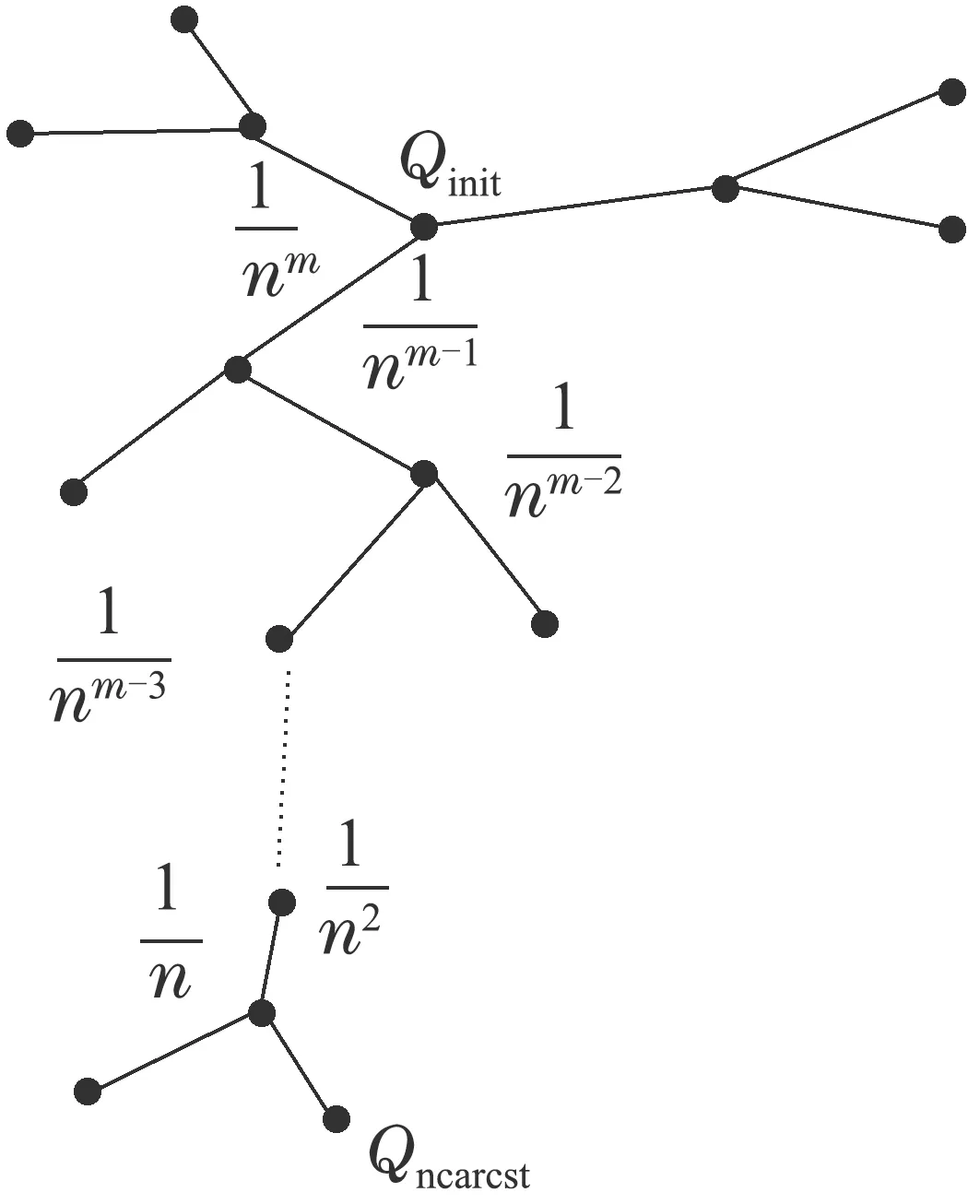
图2 碰撞检测机制示意图Fig.2 Schematic diagram of collision detection mechanism

以节点在其子节点方向上的碰撞概率来决定路径的扩展方向,g值越大,表示在该方向上遇到障碍物的可能性越大;反之,在该方向上遇到障碍物的可能性越小.在考虑全局碰撞信息后,优先选择g值较小的方向作为随机树的下一步扩展方向.改进的快速随机生成树算法(goal biasing collision rapid-exploration random tree,GBC–RRT)算法用图2所示的碰撞信息检测函数优先选择随机树的扩展方向,从而代替经典RRT算法随机扩展的方式,提高了路径寻优的效率.基于期望时间下的移动机器人目标搜索路径规划算法的伪代码如下:

上层规划是序列规划,属于在拓扑图中进行图搜索,旨在根据最优期望时间规划生成观测点访问序列,上层规划给出了概要的路线,但是该路线不适于机器人跟踪.故下层规划采用GBC–RRT算法生成了适合移动机器人跟踪的局部路径.期望时间下的移动机器人目标搜索路径规划示意图如图3所示.

5 实验结果与分析

为验证本文所提搜索策略的有效性,首先在拓扑点规划将本文所提算法与贪心算法(greedy algorithm)比较,然后在P–P规划方面,将RRT算法和GBC–RRT算法比较,分别将这两种算法应用于“T”形图、“V”字形、“一”字形、“U”字形的路径规划,本文重点在于运动规划问题,故目标概率采用人工经验值.因环境与搜索结果相关性高,故采用多种目标环境分步进行测试.

“T”字形对应环境中的客厅障碍物空间,“V”字形对应环境中不规则可行空间,“一”字形对应环境中难以检测到入口的狭窄通道,“U”字形对应环境中容易产生局部极小的陷阱问题,将RRT算法和GBC–RRT算法应用于“T”字形、“V”字形、“一”字形、“U”字形,仿真结果如图4–7所示,两种环境下RRT和GBC–RRT对应的运行时间、节点数和路径长度见表1.

图3 期望时间下的移动机器人目标搜索路径规划Fig.3 Path planning of target search for mobile robot with expected time

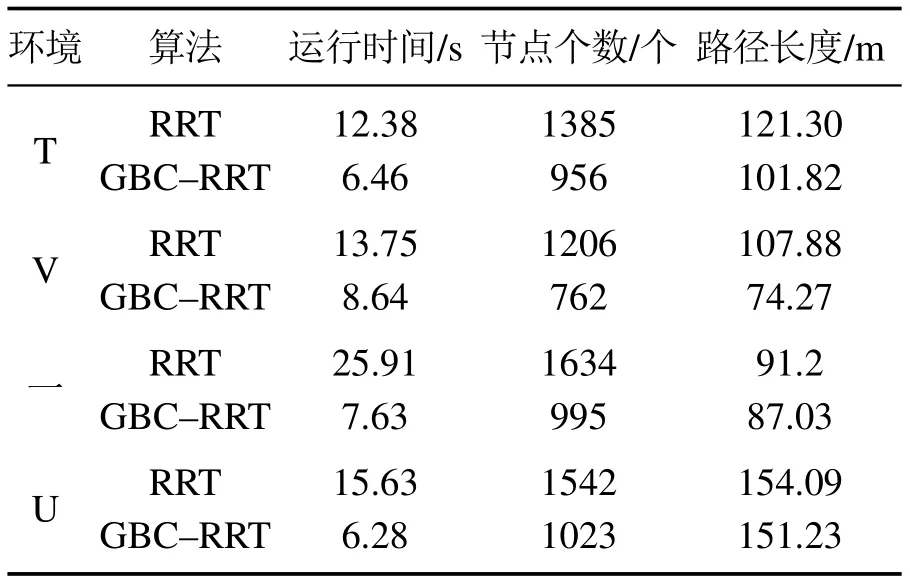
表1 环境1下特殊情况仿真结果Table 1 Simulation results under special circumstances in E1

由图4–7可见,经典RRT算法随机树扩展区间更大,复杂度更高,目标偏向性差,导致路径成本比较高.经典RRT算法没有考虑非完整约束,规划出的路径状态转变较快,往往存在角度突变的情况,这对移动机器人来说难以跟踪.GBC–RRT算法随机树探索的区间小、复杂度低、目标偏向性强,并且GBC–RRT算法在规划过程中考虑了非完整约束,规划出的可执行曲线比较光滑,不存在状态突变的情况,机器人可以在该轨迹上直接跟踪.由表1可见GBC–RRT算法在运行时间、节点数、路径长度方面都比RRT算法占优.

图4 T形环境下测试Fig.4 Test in a T-environment

图5 V形环境下测试Fig.5 Test in a V-environment

图6 “一”形环境下测试Fig.6 The test in a environment with a narrow gap

图7 U形环境下测试Fig.7 Test in a U–environment

观测点的访问顺序不同会导致期望时间存在一定的差异.以简单搜索任务为例说明:假设搜索任务的工作环境如图8所示,蓝色区域表示不可行空间,其余区域表示可行空间,X1,X2,X3,X4为观测点.观测点的选取原则是尽可能少的点覆盖整个工作环境,观测点的数量越多对工作环境覆盖效果越好,但会增加重叠区域,不利于优化,本文分别采用4个和10个观测点,按观测点的选取原则置于工作环境S内.任务要求:机器人从起点开始按照最优期望时间遍历每个观测点对工作环境S存在的目标进行搜索,最后携带所得目标返回起点.分别测试贪心–RRT(GA–RRT)算法、贪心–GBC–RRT算法和本文所提算法对搜索目标期望时间的优化效果.对于复杂的任务搜索路径规划,为避免机器人本身对问题分析的影响,采用膨胀处理的方式,不考虑移动机器人的大小和形状,把移动机器人作为质点处理[5].算法中ρa值取0.05,观测点概率均按照表2中所示的经验值设置,分别采用贪心–RRT算法、贪心–GBC–RRT算法和本文所提算法对移动机器人进行路径规划,生成的路径及数据如图9–11,表3所示.由图9–10可见,根据贪心算法可得X1–X3–X2–X4–X1节点顺序,在节点之间分别用RRT,GBC–RRT算法得到了局部路径,由表3可见,贪心–RRT 算法得到的期望时间为60.54 s,运行时间为22.32 s,贪心–GBC–RRT 算法得到的期望时间是57.78 s,运行时间为16.30 s.由以上结果可见,GBC–RRT算法在期望时间这一指标上并未发生显著变化,但是在运行时间方面有较大的提升,显著改善了算法的实时性,本文所提算法所获结果的期望时间为49.59 s,运行时间为14.86 s,在期望时间指标上有明显优势,提高的百分比为18.09%.

图8 移动机器人路径规划工作空间Fig.8 The workspace for mobile robot path planning

表2 环境2下目标点在观测区域的概率分布Table 2 Probability distribution of target points in the observation area of E2

图10 环境2下贪心GBC–RRT的多目标搜索Fig.10 Multi-target search path generated by GA–GBC–RRT in E2

图11 环境2下最优期望时间的多目标搜索Fig.11 Multi-target search with optimal expected-time approach in E2

表3 环境2下3种算法指标的对比Table 3 Comparison of three algorithms in E2

为进一步验证改进算法的有效性,将观测点的数量增为10个,记为E3,增加3组对比实验,ρa取0.05,各个观测点对应的概率如表4所示.重复以上实验,仿真生成路径规划如图12–14和表5所示.图12–13为贪心式算法生成的节点访问顺序,其结果为X1–X9–X2–X7–X10–X4–X8–X6–X5–X3–X1,节点之间分别采用RRT和GBC–RRT进行局部路径规划,图14是根据改进改良圈生成的节点访问顺序,其结果为X1–X3–X5–X6–X7–X10–X8–X9–X4–X2–X1,节点之间同样采用GBC–RRT算法进行路径规划.由表5可见,按照贪心算法生成的节点顺序,即使局部路径采用GBC–RRT算法,期望时间没有明显的提高,但其在运行时间得到了改善.在期望时间这一指标上,本文所提算法路径规划的期望时间显著缩短,提高了约50%.

表4 环境3下目标点在观测区域的概率分布Table 4 Probability distribution of target points in the observation area of E3

图12 环境3下贪心RRT的多目标搜索路径Fig.12 Multi-target search path generated by GA–RRT in E3

图13 环境3下贪心GBC–RRT的多目标搜索路径Fig.13 Multi-target search path generated by GA–GBC–RRT in E3

随时间推移,目标在观测点的概率会发生变化,由式(7)得到表6所示对应概率.采用本文所提算法得到路径规划如图15所示.由图15可见,当概率发生变化时,观测点访问序列会发生变化,进而导致整体路径规划结果的变化,例如:在环境3下的节点访问序列为X1–X2–X3–X4–X5–X6–X7–X8–X10–X9–X1,当该环境的目标概率发生更新后,节点序列随之发生变化,整体路径的期望时间也由26.08 s变为39.64 s.

图14 环境3下最优期望时间的多目标搜索路径Fig.14 Multi-target search with optimal expected-time approach in E3

表5 环境3下3种算法指标的对比Table 5 Comparison of three algorithms in E3

表6 环境3下更新后目标点在观测区域的概率分布Table 6 Updated probability distribution of target points in the observation area of E3

图15 环境3下概率更新后的多目标搜索路径Fig.15 Multi-target search path with updated probability in E3

重复进行50次实验,得到如图16–17所示多次实验与期望时间、运行时间曲线图.根据统计学的方法,计算期望时间的平均值为26.80 s,运行时间的平均值为17.29 s,期望时间的标准差是1.07,运行时间的标准差为1.27.根据期望时间、运行时间的平均值能说明50次实验结果下期望时间大小主要集中在26.80 s、运行时间主要集中在17.29 s.期望时间、运行时间的标准差越小说明数据的离散程度较小,改进算法的稳定性较高,数据有较小范围的波动,存在一定的波动源于RRT算法本身节点生成过程的随机性.

图16 环境3下50次实验的期望时间Fig.16 Expected-time of 50 tests in E3

图17 环境3下50次实验的算法运行时间Fig.17 Run time of 50 tests algorithm in E3

为了测试目标偏好参数ρa对模型的影响,在复杂环境下分别将ρa调小至0.005和将ρa调大至0.5,观测点概率保持不变,重复进行实验,仿真结果如图18–19所示.由图18–19可见,当ρa越小,随机树扩展的随机性越强,目标的偏好性越低,会出现冗余的搜索,降低了多目标搜索的效率,反之,随机树扩展的随机性越弱,目标的偏好性越高,出现冗余的搜索较小,提高了搜索效率.ρa参数的改变,生成的路径变化幅度小,验证了目标偏好值的大小对目标搜索时上层路径规划的影响不大.

为了得到更多ρa值下路径规划的期望时间,以步长为0.03在[0.01,0.58]区间内依次取值,得到图20所示的期望时间曲线图.综上所述,目标参数的改变影响了观测点间的局部路径规划,当目标偏好参数越大,随机树扩展的随机性越低,目标的偏好性越高,运行时间变化显著,但是当目标偏好参数选择足够大时,仿真实验时规划算法容易陷入局部极小值;当目标偏好参数越小,虽能避免局部极小值问题,但是随机性强,目标的偏好性较差,需要更多的时间来搜索节点,直接表现为仿真运行时间会更长.因此,需要根据环境的复杂性,进行偏好参数调节.目标偏好参数变化属于下层局部规划部分,只影响下层规划,对上层规划的序列没有影响.

图18 环境3下ρa=0.005的路径规划Fig.18 Path planning in E3 with ρa=0.005

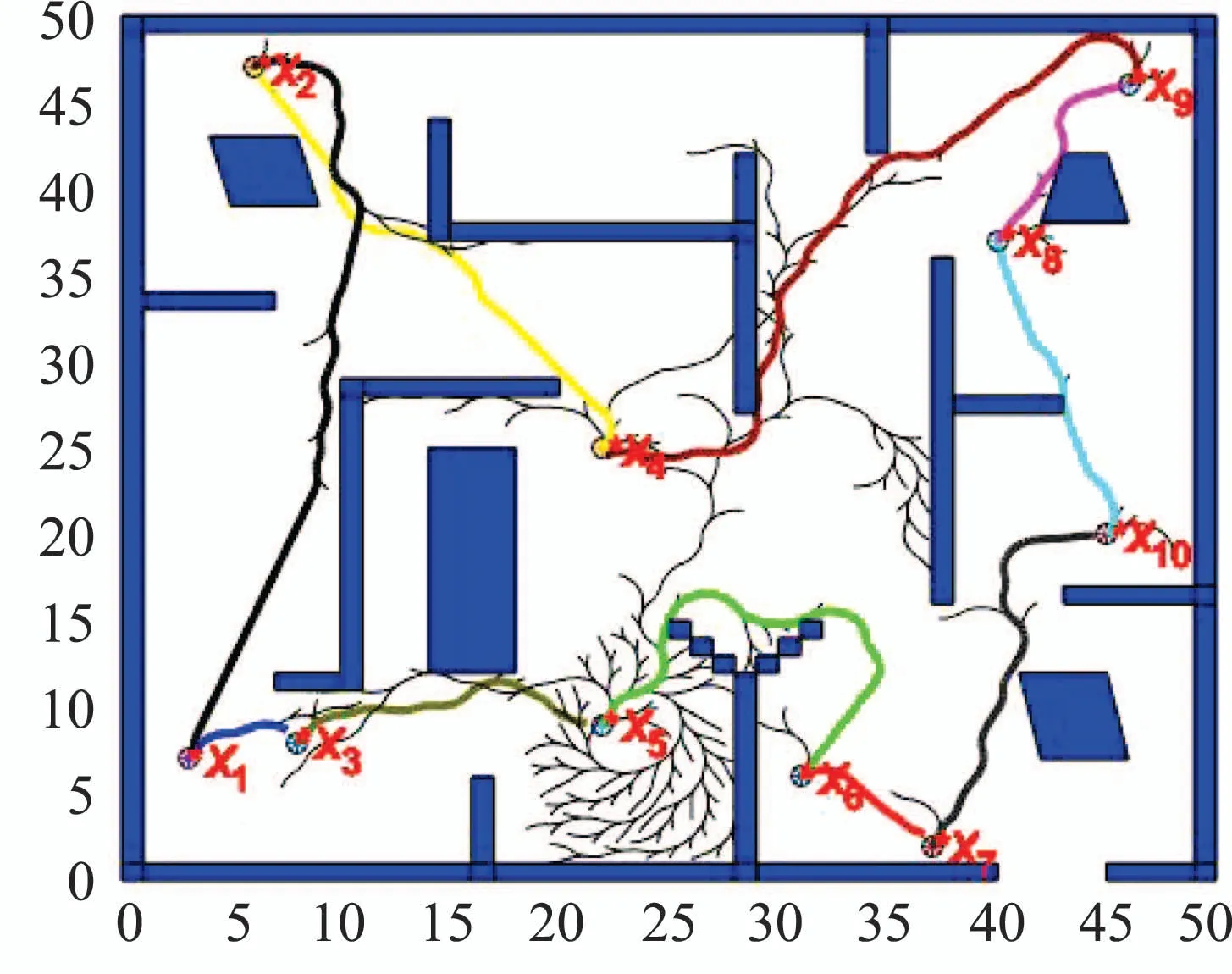
图19 环境3下ρa=0.5的路径规划Fig.19 Path planning in E3 with ρa=0.5

图20 不同ρa值下期望时间曲线Fig.20 Expected-time curve for ρa

6 结论

为了解决不确定环境下多目标搜索效率低的问题,本文提出了一种基于最优期望时间的目标搜索路径规划方法.通过引入一种新的观测点,构建非均匀分布概率测算模型,在上层序列规划采用改进的改良圈算法优化观测点序列,比常用的贪心算法具有更强的全局优化能力;下层采用GBC–RRT算法进行节点间路径规划,相比于经典RRT算法具有更好的目标趋向性.实验结果表明,该方法可以显著缩短移动机器人获取目标的期望时间,适用于以期望时间为指标的单机器人多目标搜索取回任务,在部分其它任务模式下虽可生成可行路径,但优化效率会有所降低.