KELM-TE方法在石油储运系统安全信息风险传播中的应用
2020-08-14罗通元
罗通元,吴 超
(1.西安石油大学电子工程学院,陕西 西安 710065;2.中南大学资源与安全工程学院,湖南 长沙 410083;3.中南大学安全理论创新与促进研究中心,湖南 长沙 410083)
当今世界处于信息化大发展大变革的时代,信息在时空传播中对管理提出了模式变革的思维创新要求[1],伴随着信息时代的快速发展,信息也越来越凸显其重要性。石油化工企业生产系统过程工艺条件严苛,生产活动中常伴有高温、高压和高振动等影响因素,其正常运行会直接影响到石化企业的生产和安全状态。生产系统发生事故时的安全信息常呈现出非线性、非平稳性的特征,难以精确稳定地识别和掌握安全信息的传递路径,由此带来的信息风险也表现出一系列随机状态。在石化企业中,一旦发生某系统的故障和事故往往会波及到邻近设施和系统,同时系统内单元之间存在直接联系,单元之间的相互依存关系使得某一事故信息会沿着传递效应路线进行信息衍生传播,由此会带来难以估量的安全信息灾难,引发连锁事故或次生事故。为了有效地控制生产系统安全信息风险的扩散与传播,确保安全生产,对生产系统内安全信息风险传播路径进行研究就显得尤为重要了。
目前对于生产系统安全信息风险传播路径的分析主要是针对事故原因信息的分析,涉及的信息耦合和信息传播较少[2]。关于事故中安全信息的剖析主要是基于传统事故致因模型、过程知识模型和过程数据模型三大类方法。其中,基于事故致因模型的安全信息分析最常见,如Ashenden[3]最先提出了基于信息不对称的事故预防技术,揭示出信息安全管理者、高层领导者和底层员工之间存在客观的信息代沟,即双方及三方在信息理解上存在的不对称。事故预防的关键技术为人类进一步认识安全信息传播风险提出了新思路,如邹铁方等[4]利用收集的事故现场人体损伤、车辆破坏及环境等信息,通过响应曲面法与蒙特卡罗方法模拟出人-车事故再现场景;赵潮锋等[5]提出了安全信息缺失的概念和事故致因理论,但主要是以人的不安全行为与物的不安全状态的轨迹交叉为基础,且缺乏对致因因素之间数学关系的刻画;Leveson[6]提出了基于安全信息流动的系统理论和事故过程模型,模型的本质是基于人的信息处理过程,但未将系统中其他因素作为安全信息的核心要素;毕远志等[7]针对目前建筑工程施工现场人流、物流及信息流交汇的特点,提出了用安全信息定置管理技术来解决建筑施工安全难题的方法;罗通元等[8]首次构建了基于安全信息认知的事故致因模型,并指出安全信息的衰减、延迟、干扰、失真和空间错位等是导致事故发生的根本原因。事故致因模型的研究主要以信息维度去研究安全问题,但是对于安全信息认知事故致因机理的研究还不够深入,并且构建的事故致因理论也存在自身缺陷,最主要的问题是传统事故致因模型不能全面地反映安全信息在事故中的作用及机理。基于过程知识的建模分析包括符号有向图、因果模型和多层流模型等[9-11],如姜英等[12]提出了一种基于复杂网络理论构建层次符号有向图网络模型并识别关键节点的方法,该方法通过选取度中心性、接近中心性等多个节点重要性评价指标,采用主成分分析法确定各指标权重并进行综合评价排序,进而在子系统网络模型中确定出关键节点的位置;张挺等[13]通过动态因果模型分析,计算了各连接的超越概率,并构建出视觉工作记忆任务的脑效应网络;张少民等[14]采用多层流模型对煤层注水系统进行建模,描述了目标与功能之间的相互关系,表达出了注水系统的子系统时间节点和时间段,为研究系统可靠性并发现系统薄弱环节提供了基础。基于过程知识的建模方法能够对规定变量的因果关系以图形化的简单形式加以呈现,给人以直观和简单的印象,但是却难以实现定量化描述,定性的主观因素会直接影响变量之间的关联关系。基于过程数据的建模分析主要依赖一些常用函数,如互相关函数、贝叶斯网络等[15-16],但贝叶斯网络的概率设置需要依赖主观经验,存在较大的误差。
根据以上分析可知,现有的研究大多是根据事故的原因进行分析,缺乏对安全信息传播过程的研究。本文通过文献调研,认为基于信息熵的传递熵(TE)方法可用于分析变量间的非线性相关关系,通过计算变量间的传递熵就能分析过程变量间由于信息传递所带来的因果性[2],在此基础上还需要对安全信息传播过程进行预测与预防。传统的安全信息传播过程预测模型主要基于线性回归,需要假设被预测数据遵循目标函数形式,但由于生产过程安全信息十分复杂,这种假设可能会出现较大的误差。此外,非参数模型的常用机器学习算法如人工神经网络和支持向量机会出现训练速度慢、过拟合和多参数过程等问题,而核极限学习机(KELM)集成了两种算法的优点,具有快速学习和强泛化的特征。因此,本文提出了一种基于核极限学习机和传递熵结合的生产系统安全信息风险传播路径分析方法(简称为KELM-TE法),针对某一信宿扰动或异常分析安全信息的风险传播过程。为了便于本方法的应用,将石油生产系统中的石油储运系统作为研究对象,建立了石油储运系统安全信息风险传播模型,并预测了安全信息风险传播可能的路径,为及时发现并控制安全信息传播溢散现象、保障石油储运系统安全运行提供方法指导。
1 基本理论
1.1 极限学习机和核极限学习机
极限学习机(Extreme Learnine Machine,ELM)是一种简便、高效的单隐层前馈神经网络学习算法。该算法相较自组织映射网络、K均值法和神经网络等算法具有网络结构稳定、泛化性能好等优点,因而广泛适用于分类器设计中。根据ELM速度快的特点,它可以提高整个网络的学习效率,同时在应用中只需要网络的隐含层节点个数,通过随机分配输入权重和隐含层偏置,就能得到唯一的最优解[17-18]。ELM由输入层、隐含层和输出层组成,层与层之间通过神经元连接,其结构模型见图1。其中,n为隐含层节点数;ωi和βi分别为连接输入层和隐含层、隐含层和输出层的权重矩阵;xj、zj分别为输入和输出;bi为隐含层的阈值[19]。该算法的原理如下:对于给定N个不同数据样本(xj,ui),其中xj=[xj1,xj2,…,xjm]T∈RN,xj为一个m维输入样本;ui=[ui1,ui2,…,uim]T∈RN,ui为xi对应的期望输出值。
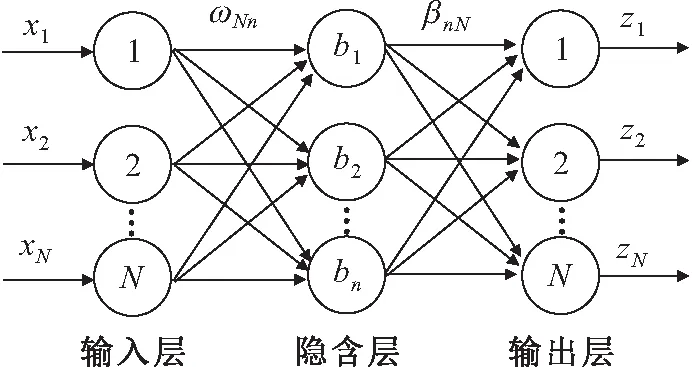
图1 极限学习机(ELM)网络结构模型Fig.1 Structure model of Extreme Learning Machine (ELM)
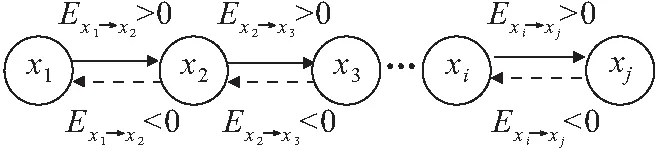
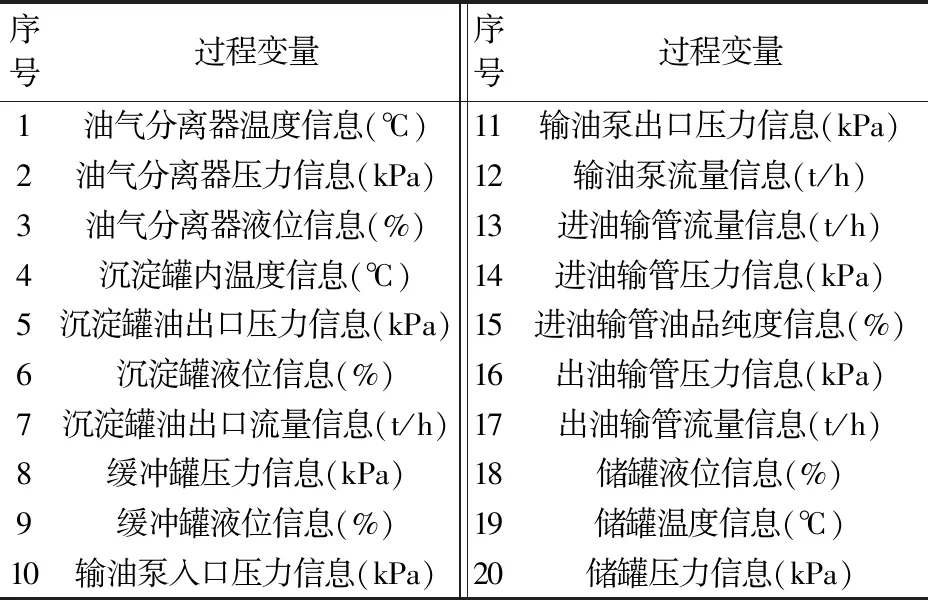
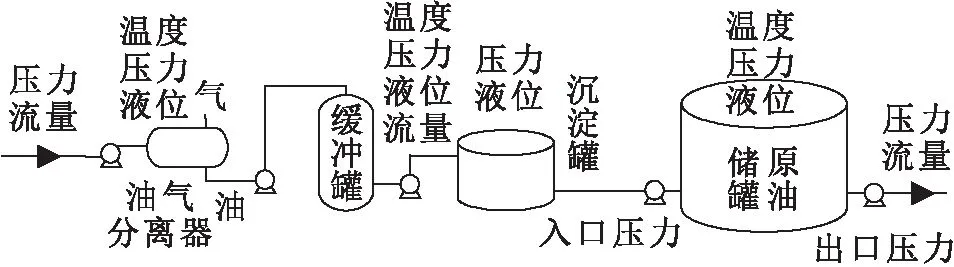
具有n个隐含层节点(n (j=1,2,…,N) (1) 式中:βi为第i个隐含层节点的输出权重;gi为激活函数;ωi=[ωi1,ωi2,…,ωim]T为第i个隐含层节点的输入权重;xj为输入向量;bi为第i个隐含层节点的偏置;zj为ELM网络的实际输出值。 根据实际输出值zj和期望输出值ui就可以得到学习目标值,即ELM网络学习的最小误差为 (2) 根据矩阵原理,公式(1)可简化为Hβ=U(其中,H为ELM的隐含层输出矩阵;β为输出权重矩阵;U为期望输出矩阵),ELM的隐含层输出矩阵的表达式为 (3) 为了获取更具有鲁棒性和泛化能力的ELM,提高模型的稳定性,有必要摆脱隐含层节点激活函数g(x)的形式困扰,那么可以把g(x)的内积形式以核函数的形式表达出来。这样就使核极限学习机(Kernel Extreme Learning Machine,KELM)算法中,函数g(x)的具体形式不用给出,只需要知道核函数K(xi,xj)的具体形式就可以求出输出函数的值,且隐含层节点数能够自适应确定。在核函数形式确定的前提下,将每两个样本之间进行一次核函数映射得到线性内积的点的集合称为核矩阵ΩELM,设隐含层节点数为n,有N个训练样本,那么KELM算法中的核矩阵公式可表示为 ΩELM=HHT=h(xi)·h(xj)=K(xi,xj) (i,j=1,2,…,N) (4) 核矩阵ΩELM替代ELM算法中的随机矩阵HHT,利用核函数将n维输入样本映射到高维隐含层特征空间。核函数K(xi,xj)是核矩阵ΩELM的第i行第j列的元素,通常包括RBF函数、线性核函数和多项式核函数等。一般利用RBF核函数计算权重向量:β*=HT(I/C+HHT)-1U(其中,I为单位对角矩阵;C为惩罚系数),那么KELM的隐含层输出矩阵的表达式为 (5) 从生产系统宏观角度看,系统过程是信息熵增加的过程,始态就是系统信源的产生,终态是系统崩塌的发生,该过程是自发的、单向的和不可逆的过程。从生产系统安全维护来看,系统中的信息由无序到有序的现象可以称为安全信息的自组织现象。自然无人干预的系统必将是信息熵增的系统,系统客观表现出开放性、动态性、不确定性、不可逆性和突变性等特点。 熵的概念最早出现于热力学,热力学第二定律指出:在有限时间和空间内一切和热现象有关过程的发展都有其自发进行的方向[20]。信息论创始人Shannon[21]借鉴热力学中“熵”的概念,把信息中排除了冗余后的平均信息量称为“信息熵”,并给出了计算信息熵的数学表达式。根据信息熵的定义,把信息的多少看作是一种消除不确定性的度量,即所得信息越多,其事物不确定性就越小,无序度(混乱度)就越小,熵就越小,表现在宏观上就是系统越稳定,反之亦然[22-23]。系统的安全状态取决于安全信息熵的状态,安全信息熵越小,系统越稳定,系统则安全无事故;安全信息熵越大,系统越不稳定,系统则必出事故。这里的系统指的是保持完整的功能和结构,并且具有畅通的内外信息流、物质流和能量流的有机整体。如物质生产系统和城市群运行保障系统等。由此可将安全信息熵简单理解为安全信息混乱的程度。因此,系统中的安全信息不断趋向混乱的过程可以用信息熵来刻画。 可以结合相关学科理论对熵进行研究,但是安全科学与熵的结合研究相对较少。熵是状态函数,熵变(ΔS)只取决于体系的始态与终态,与过程无关。一个系统熵的变化有两部分:一部分是由外界环境输入的熵叫熵流;另一部分是系统本身内部产生的熵叫熵产。熵流可以大于、等于或小于零,而系统内部产生的熵则永远只能大于或等于零。对于孤立体系,系统的熵只能向着熵增加的方向运动[24]。许多研究利用信息熵算法只能反映单一时间序列的整体复杂程度,但无法反映多时间序列之间随时间变化的耦合关系。而基于信息熵的传递熵(Transfer Entropy,TE)算法通过量化两个系统间的信息传递,将信息熵理论从只表示大小的标量扩展到既表示大小又表示方向的矢量,进而实现表征两个系统间的耦合关系[25-26],这种基于概率分布、信息熵和统计方法的算法可用于表征变量间的非线性相关关系和两变量间的信息传递方向。 信息熵是信息论中用于度量信息量的概念[2],其定义为 Hx=-∑xp(x)log2p(x) (6) 式中:Hx表示变量x的信息熵;p(x)表示变量x的概率分布。 根据信息熵的定义,可将变量y到变量x的传递熵定义为 (7) 两个变量x和y的信息熵大小可用联合信息熵Hxy来表示,其定义为 Hxy=-∑x,yp(x,y)log2p(x,y) (8) 其中:p(x,y)表示变量x和y的联合概率分布。 度量信息量后还需要刻画信息之间的相关性指标,这就要涉及到互信息的概念[27]:互信息是表示两个变量或多个变量之间共享的信息量。要摒弃传统互信息具有数据信息匮乏、传递和反馈时效性差、决策效率低下等特点[28],选择的互信息越大,变量之间的相关性越强。连续型随机变量x和y之间的互信息可定义为 Ixy=∑x,yp(x,y)log2p(x,y)/p(x)p(y) (9) 式中:p(x,y)表示变量x和y的联合概率分布;p(x)和p(y)分别表示变量x和y的边缘(概率)分布。 连续型随机变量x和y之间的互信息定义表示若已知变量y的值,关于x知道的信息量是多少。从该定义可以直观地看出,若变量x和y相互独立,则互信息Ixy为零,也就是说若已知变量y,关于x所知的信息量为零。传递熵TE可作为变量间因果关系的指标,因而对于非线性的生产系统更具适用性。 以上介绍了TE的基本原理,根据其优点可以广泛应用于自动化、规模化及大数据的生产系统中,目前其应用领域已经拓展到各行各业,并在处理生产系统中各类安全信息及数据中发挥了重要作用。它以变量间的安全信息量传递为基准,在非线性的安全信息系统内更具有适用性。而KELM在权重计算方面的优点为神经网络在安全信息风险指标管理方面提供了可借鉴的思路。两者相互结合可使安全信息的风险传播得到有效预控,为安全信息的研究拓展了新思路。 石油储运系统是石油石化行业的重点管控对象之一,也高危行业管理中的重中之重。石油储运系统一直被各种异常、故障和事故所困扰,由此带来的人身伤害、财产损失和环境污染问题屡见不鲜。通过信息的视角可以解读该系统内安全信息的流动过程。当石油储运系统的任意部位出现异常工况时,必然有信源(石油储运系统)安全信息的释放和扰动作用,原始安全信息会沿着信道传播,在传播过程中势必会受到信噪的干扰,信道自身缺陷也会导致安全信息的衰减和缺失,这些失真的安全信息通过各种形式演化为信宿(人)可感知到的感知安全信息,进而加工形成认知安全信息,最终的信息就是人所理解的各类警报及提示信息。这一过程看似简明,实则存在复杂的信息耦合和干扰传递现象。这是因为系统内外并非呈现完全封闭的线性特征状态,系统内单元设备之间的关联性和系统外生产流程的关联性均会使得初始的异常安全信息发生衍生传播,并且影响大量相关的过程因素,如此以来势必导致安全信息风险膨胀并发生严重事故,那么这些影响安全信息风险扩散的中间因素的关联性就值得研究。如果安全信息的传播路径能够及时地被控制,那么,这种控制对于事故预防会起到决定性的作用。因此,研究安全信息风险传播路径势必成为石油储运系统风险控制的首要任务。据此,本文提出了一种基于KELM-TE结合的生产系统安全信息风险传播路径分析方法,针对某风险传播过程建立石油储运系统安全信息风险传播模型,从而实现安全信息风险传播路径的预测,为安全信息控制提供保障。 石油储运系统涉及的设备多样,工程流程较为复杂,设备的控制变量之间具有较强的关联性,系统面临着复杂的环境威胁,存在高温、高压、腐蚀、破裂和爆炸等一系列危险考验,而要搞清变量间的关联性需采用TE方法推演出各变量之间的关系。 简言之,石油储运系统中涉及的各类泵、压缩机、管道、阀室和辅助动力等子单元都是安全信息潜在的信息源,也扮演着安全信息风险传播的角色。其中各类控制和监测变量繁多,互相牵连影响复杂,故对于这些过程变量的影响判断至关重要。根据前述可知,如果分析变量x和变量y之间的影响程度,可以通过计算两变量间的传递熵来实现。假设变量x是初始变量,y是中间变量,那么由公式(7)可计算出变量y到变量x的传递熵Ey→x。Ey→x实质为y的信息对于x不确定性大小的影响,也就是y传递给x的信息量的大小,其可作为衡量变量x和变量y之间因果性的指标。 求得传递熵之后,就明确了变量间的因果关系和传递信息量,但如何确定变量间的相关程度,以便确定因果性最强的变量群,则需要确定两变量间的关联系数。根据文献[28],常用统计方法来计算两变量间的关联系数,其计算公式为 (10) 上式说明:如果μx,y=Ey→x,表示变量x和y之间的传播方向为y到x;如果μx,y=Ex→y,表示变量x和y之间的传播方向为x到y;如果μx,y=0,表示变量x和y之间没有因果关系。由于每两个时间序列可以得到一个确定值,但是如果两变量相互之间的传递熵相差无几的话,就无从确定因果性,因此需要设置合适的阈值对两变量间因果关系的显著性水平进行检验[2]。通过公式(7)计算每两个变量间的传递熵值,求出所有传递熵绝对值的均值ωEx→y和标准差σEx→y(ωEy→x为变量y到x方向关联系数的平均值;σEy→x为变量y到x方向关联系统的统计标准差),并通过计算阈值,进而可以判断出两变量间因果关系的显著性。若关联系数没有通过显著性检验,表明两变量间不具备因果性[28]。阈值的计算公式如下: |Ex→y|-ωEx→y≥6σEx→y (11) 对于本例中的n个过程变量x1,x2,…,xn,就可以利用上述方法计算两两变量之间的传递熵,确定两变量间的关联系数和传播方向,这样就可确定出相应的变量携载的安全信息风险传播模型,再通过过程知识进行修正。安全信息的风险传播推演模型简要表达,见图2。 图2 安全信息的风险传播推演模型简图Fig.2 Brief diagram of risk propagation reasoning model for security information 注:箭头表示安全信息风险传播方向;若Exi-xj>0,说明箭头由xi指向xj,即传播方向为由上级变量指向下级变量,反之,则传播方向相反。 确定安全信息的风险传播路径前,需要划分单元并建立模型,这是后续分析的基础。石油储运系统过程变量中发生的异常通常由直接影响的变量扰动所引起。为了控制安全信息风险的失控传播,提出安全信息风险传播分析方法至关重要,本文根据文献[2],提出了一般的安全信息风险传播路径分析流程如下: (1) 路径图的确定。当某一过程变量发生安全信息时,将其作为上级变量,分析与其直接相连的下级各过程变量,建立变量间的安全信息风险路径图。 (2) 扰动变化率的计算。确定了信源变量与各下级变量间的路径关系,需要根据上级变量与下级变量间的扰动性确定下级变量受影响程度的大小,而通过扰动变化率的计算,可以反映出各下级变量受上级变量扰动的影响程度。对以时刻tm为中心,以[tm-n,tm+n]为时间间隔的变量xi的时间序列进行最小二乘拟合,求得斜率的绝对值τi即作为变量xi的扰动变化率,其计算公式为 (12) 式中:xim为变量xi的第tm个时刻的变量值。 (3) 影响因数的计算。由上述两变量间的关联系数和变量扰动变化率公式,可计算出上级变量对各下级变量的影响因数Ri,其最大值可作为最终衡量受上级变量影响最大的下级变量的判别依据。影响因数Ri的计算公式为 Ri=(1-e-τ|τi|/1+e-τ|τi|)μxi,yi (13) 式中:τ为调整参数,取值为2 000;μxi,yi表示变量xi和yi之间的关联系数;τi表示变量xi的扰动变化率。 为了确定出受影响的下级变量,如果计算的影响因数小于阈值,那么就不能将该变量考虑进去。这里的阈值取历史统计与专家经验值,一般设为1.75。 (4) 重复上述步骤(2)、(3),则可依次确定出受上级变量影响的各下级过程变量,并最终形成完整的安全信息风险传播路径。 石油储运系统是石油石化产业链中的重要关键系统之一,一般来说石化企业的石油储运系统庞大复杂、点多面广,主要由原油库系统、储罐系统、长输管道系统、仪表系统、动力系统等组成。随着国家石油需求量的激增,石化企业面临更多艰苦的生产和安全任务,石油储运系统也时常发生系统设备事故或故障。石油储运系统中的腐蚀监测与评价、储运过程中的油气蒸发损耗与回收、过程节能与环保等问题中释放的安全信息一直都是治理的重点对象。石油储运系统内的储罐涉及的管道单元是系统的重要部分,由上游生产系统输送的石油产品从入罐管道进入储罐,管道凝管和腐蚀等故障信息是输油过程中常常发生的现象之一,导致这些故障或事故的主要原因在于输油介质的密度、温度、压力和杂散电流等信息意外释放导致。此外,储罐系统中储油发生增压、高温和超液位等信息扩散也会严重影响储罐安全,可能出现冲顶、憋压裂纹、罐盘损坏、泄漏、起火爆炸和机泵故障等灾难性事故。为了保证储运系统中安全信息得到控制,降低或消除信息风险带来的事故,本文利用KELM-TE方法,针对某油田联合站储运系统内的储罐单元进行安全信息风险传播路径分析。 首先需要对储运系统进行单元划分,储罐单元主要由油气分离器、沉淀罐、缓冲罐、进油输管、储油罐、出油输管和输油泵等组成。本文针对某油田联合站储罐单元憋压泄漏信息风险传播过程,建立其相关的过程变量见表1。 表1 某油田联合站储罐单元憋压泄漏风险的过程变量Table 1 Process variables of pressure leakage risk of the storage tank units in an oil field union station 根据该储罐单元憋压泄漏风险的过程变量和某油田联合站的历史统计数据,本文选取塔里木油田某联合站储罐单元各参数的监测数据5 000组,先利用公式(10)计算出两两变量之间的关联系数,再根据公式(11)计算阈值并判断两变量间因果关系的显著性,最后经修正后建立了某油田联合站储罐单元憋压泄漏过程安全信息的风险传播推演模型(见图3),并由此推演出该过程中完整的安全信息风险传播模型,两两变量间的关联系数见表2。 图3 某油田联合站储罐单元憋压泄漏过程安全 信息的风险传播推演模型Fig.3 Risk propagation reasoning model for security information in pressure leakage processes of the storage tank units in an oil field union station 表2 某油田联合站储罐单元憋压泄漏风险两两变量间的关联系数Table 2 Correlation coefficient between variables of pressure leakage risk of the storage tank units in an oil field union station 根据实际调研,以某联合站储罐单元憋压泄漏 事故为分析实例,利用安全信息风险传播搜索方法进行分析。该方法是根据安全信息过程变量间的关联系数确定变量之间的关联强度,安全信息风险传播路径的确定由安全信息过程变量组成,形成了完整的安全信息流动过程,体现信息流及流动过程的关键节点。其路径分析以某联合站储罐单元为研究对象,其示意简图见图4。 图4 某联合站储罐单元示意图Fig.4 Schematic diagram of the storage tank units in an oil field union station 现场调查显示,某公司的输油泵出口压力异常增高,泵体出现剧烈抖动和噪声,可能原因为部分流道阻塞,高压液体冲击引起储罐泄压启动,出油输管压力激增,控制系统误判储罐低液位,使得输油泵启动进而加大泵体压力和流量,缓冲罐低压警报启动增压流程,势必提高了进油输管的流量,当操作人员发现储罐憋压时已经来不及控制储罐容量,在控制系统下储罐处于高度憋压,最终导致泄漏事故的发生。最终,安全人员解决了输油泵压力增高的故障,采取措施使得储罐系统恢复了正常运行,并控制了风险的传播。本文基于上述建立的某油田联合站储罐系统憋压泄漏过程安全信息风险传播推演模型(见图3),对安全信息风险传播路径进行了分析,具体分析过程如下: (1) 由于输油泵出口压力信息异常(节点11)进而发生报警响应,将其作为上级变量,根据因果图搜索与其直接相连的下级变量为出油输管压力信息(节点16)。 (2) 通过KELM方法预测节点11发生报警后节点16的变量值,由公式(12)可计算得到各下级变量的扰动变化率,见表3。 表3 各下级变量的扰动变化率DR和影响因数RiTable 3 Disturbance rate DR and influence factor Ri of each subsequent variable (3) 根据公式(13)计算得出节点16的影响因数(见表3),并判断其影响因数值大于阈值(默认为1.75),因此可将出油输管压力信息(节点16)作为下级影响变量。 (4) 继续搜索节点16的下级变量,包括沉淀罐油出口流量信息(节点7)和输油泵流量信息(节点12),计算各下级变量的扰动变化率和影响因数值,并将最大的影响因数值对应的节点作为节点16的下级变量。通过KELM方法预测节点11发生报警后各节点的变量值,通过比较节点7和节点12的影响因数值,节点12的影响因数值是最大且大于阈值,因此将该变量作为节点16的下级变量;以此类推,继续搜索节点12的下级变量,包括沉淀罐油出口压力信息(节点5)、缓冲罐压力信息(节点8)、输油泵入口压力信息(节点10)和储罐温度信息(节点19),由公式(12)和(13)可计算得出各节点的扰动变化率和影响因数值,其影响因数最大值为1.803,对应节点8,且大于阈值,因此将该影响因数最大值对应的缓冲罐压力信息(节点8)作为下级变量;继续搜索节点8的下级变量,包括进油输管流量信息(节点13)和出油输管流量信息(节点17),由公式(12)和(13)可计算得出节点13的影响因数值为1.641,小于阈值,整个搜索到此结束。 通过将传统的回归分析引用到实例中,同样选取塔里木油田某联合站储罐单元各参数的监测数据5 000组,分析计算得出安全信息过程变量之间的关联系数,再根据人工神经网络拟合计算出20组安全信息过程变量间的因果关系,并进行变量聚类分析。根据相关关系得出的主要风险传播路径为:节点12输油泵流量信息报警响应,直接影响节点19储罐温度信息,聚类出节点12直接相关的节点为节点4、节点11和节点17,最后影响的节点为18,这与实际情况不符,其余节点影响分析也存在与实际不符的情况。通过对比实际情况可知,节点12输油泵流量过大信息直接影响节点8缓冲罐压力过高信息,而不是直接影响节点19储罐温度信息,这说明传统的风险传播路径回归分析方法存在一定的误差,而本文提出的方法更准确和可行。 (1) 通过KELM-TE方法分析了某储罐系统憋压泄漏安全信息风险传播中的过程变量,对非线性过程所分析出的安全信息风险传播路径在整个储罐系统中最可能的路径为:输油泵出口压力过高信息(节点11)→出油输管压力过高信息(节点16)→输油泵流量过大信息(节点12)→缓冲罐压力过高信息(节点8)→进油输管流量过大信息(节点13)→储罐压力过高信息(节点20)。根据实际调查,该结果验证了KELM-TE方法的有效性。 (2) KELM-TE方法根据两变量间的关联系数、下级变量的扰动变化率和变量间的影响因数可确定上下级变量间的传递关系和影响关系,进而确定了某储罐系统憋压泄漏过程中安全信息风险传播的路径和方向。该方法从与研究对象相关的内外部综合因素考虑,避免了安全信息的空间散失。 (3) 基于KELM-TE方法的安全信息风险传播路径研究可为存在复杂非线性关联性的系统提供新的风险控制策略。无论是哪种系统,只要涉及过程变量及信息传递,都可以建立相应的安全信息风险传播模型,用来预测可能的安全信息风险传播路径和方向,以便较为准确地掌握信息风险,进而提出针对性的风险控制措施。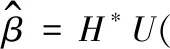
1.2 熵和传递熵
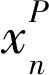
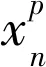
2 安全信息风险传播路径研究
2.1 安全信息风险传播推演模型的建立
2.2 安全信息风险传播路径分析
3 实例应用与分析
3.1 储运系统憋压泄漏过程安全信息风险传播推演模型建立
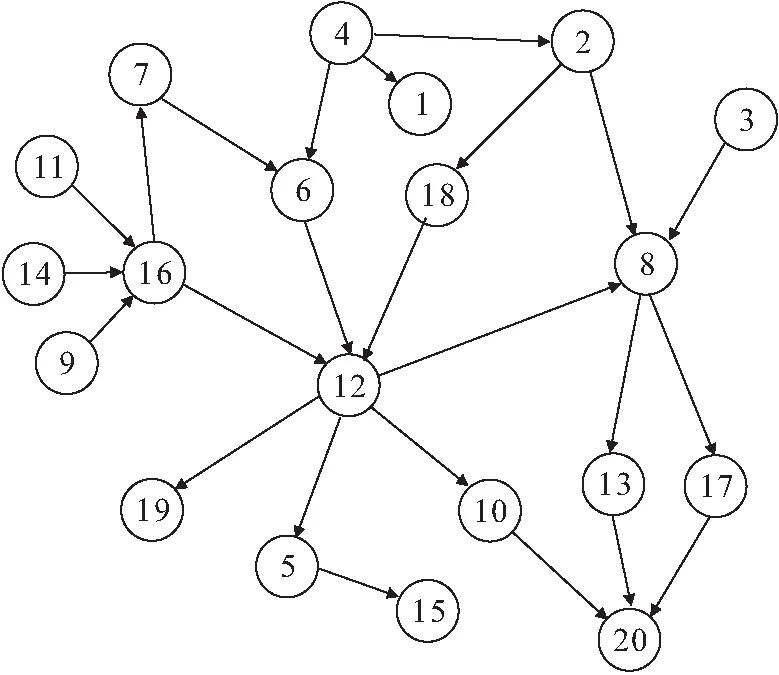

3.2 储罐系统憋压泄漏过程安全信息风险传播路径分析

4 结 论
