拱顶罐内油品蒸发损耗的数值模拟和实验研究

张佩宇，黄维秋，景海波,2，汪 城，孙宪航

(1.常州大学石油工程学院，江苏 常州 213164；2.合肥燃气集团有限公司，安徽 合肥 230075)

储罐区挥发性有机物(VOCs)的排放会引起以光化学烟雾、城市雾霾为特征的复合型大气污染问题。现阶段有效控制储罐区VOCs的排放及回收工作是我国大气环境治理领域中的热点问题[1-3]。为了降低储罐区油品的蒸发损耗，国内相关规范[4]规定储存挥发性有机液体的储罐应选用浮顶罐和集成油气回收处理系统以及密闭排气系统的常压拱顶罐。拱顶罐与油气回收集成工艺在油气排放量的最终控制、整体效益上优于单纯的浮顶罐储存工艺，是一种较为理想的轻质油品储存工艺[5]。通过对拱顶罐内油气和空气的传热和传质机理进行分析并测算油罐排气量，可为拱顶罐及其油气回收集成系统的设计和管理以及降低拱顶罐小呼吸损耗提供理论依据，以指导管理部门科学地制订相关防治方案。

国内外的研究者对油品蒸发模型进行了一些探索。目前，数值模拟已成为油品蒸发损耗的主要研究方法[6-12]。如Wang等[13]和Li等[14]研究了大型浮顶罐在不同条件下储罐油品温度和温降曲线的变化规律；Hata等[15]通过对汽车油箱进行呼吸损失测试，建立了一种汽车蒸发损耗量的估算模型；Saufi等[16]和Christian等[17]通过实验分析对液滴蒸发过程进行了研究。

上述研究均未从太阳辐射的角度对拱顶罐内、罐壁温度对储罐油品蒸发损耗的影响进行研究，为了有效地降低拱顶罐内油品的蒸发损耗，有必要对其蒸发损耗机理和评估方法展开研究。为此，本文建立了拱顶罐的非稳态传热传质理论模型，自编Matlab程序并通过自行搭建实验平台验证其可行性，对某液位为2 875 mm的1 000 m3拱顶罐在春分日6∶00～18∶00时间段储罐内油品的蒸发损耗过程进行了数值模拟，分析了储罐内温度、传热系数、液相蒸发量的变化规律，并估计了储罐的小呼吸损耗量，可为拱顶罐油品蒸发损耗的评估及其油气收集回收系统的设计、管理提供依据。

1 拱顶罐的非稳态传热传质理论模型的建立

影响储罐内油气蒸发的因素很多，本文对拱顶罐非稳态传热传质模型进行了必要的简化处理，即忽略罐内气相、液相、罐壁和罐顶的导热热阻和气相的传质阻力，分析了储罐内外的传热传质规律[18]。建立的拱顶罐非稳态传热传质模型如图1所示，外界向罐内液相、气相传递热量，同时气相向液相传递热量；液相吸收的热量全部用于自身温升和蒸发，液相蒸发即液相向气相传递质量，气相吸收的热量全部用于气相温升。

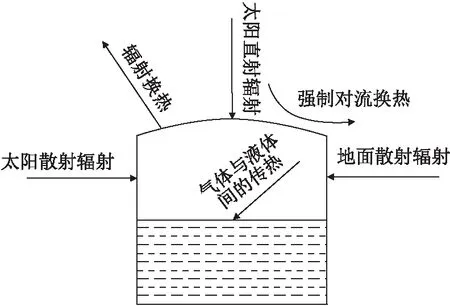
图1 拱顶罐的非稳态传热传质理论模型Fig.1 Theoretical model of unsteady heat and mass transfer in the dome-roof tank

1.1 外界与气相和外界与液相间的传热

外界向罐内气相传递的热流量(QG)包括经罐壁和罐顶传入气相的热流量。外界向罐内液相传递的热流量(QL)包括经罐壁和罐顶传入液相的热流量。由于经罐底传入罐内液相的热流量很小，所以可忽略不计。

经气体空间罐壁传入气相的热流量可按下式计算[18]：

(1)

(2)

经罐顶传入气相的热流量可按下式计算：

(3)

(4)

经液体空间罐壁传入液相的热流量即外界向液相传递的热流量(QL)可按下式计算：

(5)

(6)

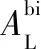
1.2 罐顶和罐壁吸收的太阳辐射量

与太阳光照射方向垂直的单位面积罐顶或罐壁吸收的太阳辐射热流密度(q0)可按下式计算：

(7)

式中:IC为太阳常数，其值为1 372.57 W/m2；P为大气透明系数，其值为0.7～0.8；σ为与昼长有关的系数；m1为与大气质量有关的系数,m1=2/cosθ；θ为太阳正午时的天顶角(°)；α为罐顶和罐壁的黑度系数。

由兰贝特定律可知，任意时刻罐壁和罐顶吸收的太阳辐射热流密度可按下面公式计算：

(8)

(9)

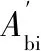
1.3 大气环境温度

一天之内大气温度变化用余弦函数表示。将起始时刻设定为日出时刻，任一时刻的大气温度可按下式计算：

(10)

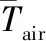
1.4 气液两相间的传热

气液两相间传递的热流量(Qin)可按下式计算：

Qin=Ainain(TL-TG)

(11)

式中:Qin为气液两相间传递的热流量(W)；ain为气液两相间的传热系数[W/(m2·K)]；Ain为气液两相界面的面积(m2)。

1.5 气相温度和液相蒸发量

由气相的热平衡可计算得出气相温度(TG)随时间的变化规律，其计算公式为：

(12)

式中:ρG为气相密度(kg/m3)；CPG为气相比热容[J/(kg·K)]；VG为气相体积(m3)；τ、τ0分别为任意时刻和初始时刻(s)；TG0为气相初始时刻温度(K)。

由液相的热平衡可计算得出液相蒸发量(m)随时间的变化规律，其计算公式为：

(13)

式中:ρL为液相密度(kg/m3)；CPG为液相比热容[J/(kg·K)];VL为气相体积(m3);h为液相汽化潜热(J/kg)；m0为初始时刻蒸发量(kg)。

1.6 气体膨胀量

常压罐呼出的混合气体体积(Vh)由两部分组成：第一部分为由于气相温升而引起的气体体积膨胀；第二部分为逸入气体空间的油气所引起的气体体积膨胀。气体空间温升而引起的气体体积膨胀累积量Vh1可按下式计算：

(14)

式中:T1、T2分别为相邻时刻的温度(K)；V为罐内气体空间体积(m3)。

逸入气体空间的油气所引起的气体体积膨胀累积量(Vh2)可按下式计算：

(15)

式中:m为某一时间段内的液相蒸发质量(kg)；M为油气摩尔质量(kg/mol)，其值为65 kg/mol；R为通用气体常数[J/(mol·K)]，其值为8.314 J/(mol·K)；P为罐内气体压强(Pa)，其值为101 325 Pa。

2 数值模拟和实验验证

拱顶罐内气相温度和液相蒸发量的数值模拟主要是基于变物性模型，通过建立拱顶罐的非稳态传热传质理论模型，并对模型进行数值求解，具体数值模拟流程见图2。

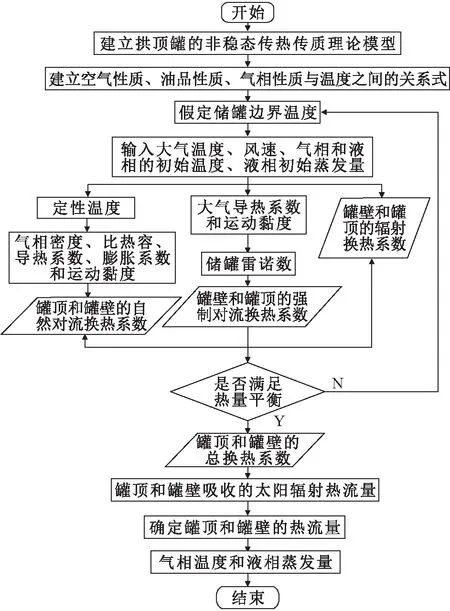
图2 拱顶罐内气相温度和液相蒸发量的数值模拟流程Fig.2 Flow chart of numerical simulation of gas phase temperature and liquid evaporation in the dome-roof tank

为了验证建立的拱顶罐非稳态传热传质理论模型的准确性，利用自制的储罐实测罐内气相温度变化并与数值模拟结果进行对比。自制储罐的规格如下：罐径D=500 mm，罐壁高度H1=500 mm，罐顶高度H2=100 mm，液位为100 mm，储罐罐顶面积和气液界面面积为0.196 3 m2，与气体空间接触的罐壁面积为0.628 m2，与液体空间接触的罐壁面积为0.157 m2，气相体积为0.085 m3。储罐内液体为92#汽油，密度为750 kg/m3，汽化潜热为3.8×105J/kg，比热容为1 821 J/(kg·K)，油品气相初始温度、液相初始温度和初始蒸发量分别为294 K、297.2 K和0 kg。

图3为储罐的小呼吸损耗实验原理图。首先将热电偶安装在储罐的罐内、罐壁和罐顶测温点上，再将热电偶与温度巡检仪连接来读取温度值。当罐内气体空间温度升高时，气体膨胀导致罐内气体外溢；当罐内气体空间温度降低时，气体收缩导致外部空气进入罐内，故可以通过气体流量计来计量气体流量。然后在罐顶开孔，利用直径2 mm的聚乙烯管通过罐顶开孔伸入罐内气体取样点进行油气取样，并利用气相色谱来测定油气样本浓度。考虑到环境风速的影响，可以使用风速仪来测量风速，即在实验开始后，每隔1个小时记录1次温度巡检仪、气体流量计和风速仪的读数，每隔2个小时对油气采样并测量其浓度。最后采用体积-浓度法按下式计算储罐小呼吸损耗量：

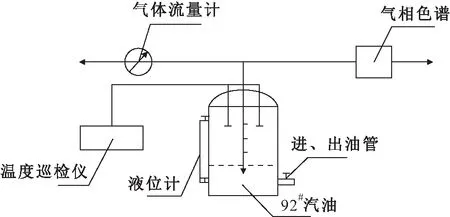
图3 储罐的小呼吸损耗实验原理图Fig.3 Experimental schematic diagram of breathing loss in the dome-roof tank

(16)

式中:ΔM为储罐的小呼吸损耗量(kg)；Vh，i为某时刻储罐呼出的混合气体积(m3)；Cy，i为某时刻储罐呼出的混合气质量浓度(g/m3)。

在环境温度和风速影响下，储罐内气体温度、气体膨胀量和小呼吸损耗量实验值与模拟值的对比，见图4、图5和表1。

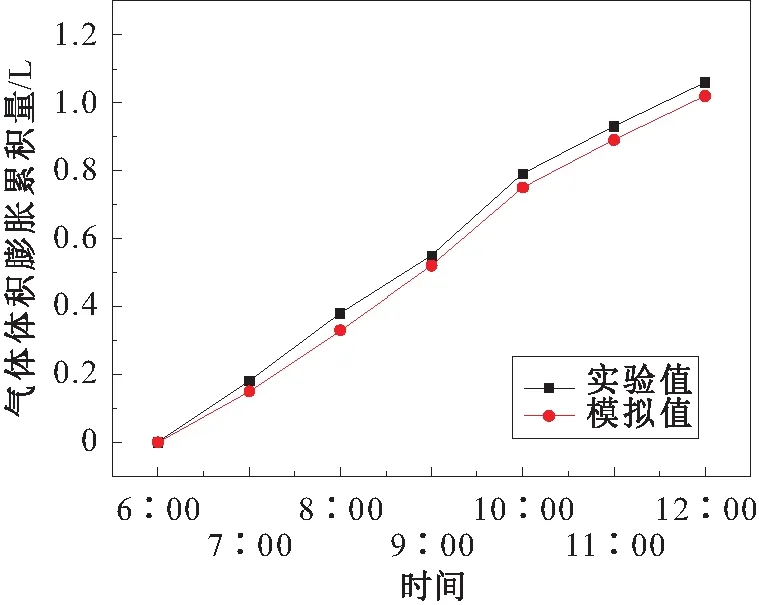
图5 储罐内气体膨胀量实验值与模拟值的对比Fig.5 Comparison of volume expansion between experimental values and simulated results in the storage tank

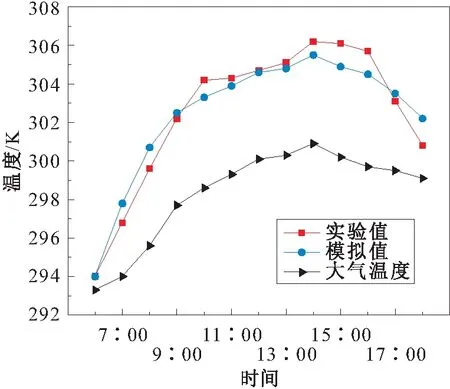
图4 储罐内气体温度实验值与模拟值的对比Fig.4 Comparison of gas temperature between experimental values and simulated values in the storage tank

表1 储罐的小呼吸损耗量实验值与模拟值的对比Table 1 Comparison of breathing losses between experimental values and simulated values in the storage tank

由图4、图5和表1可见，储罐内气体温度、气体膨胀量和小呼吸损耗量实验值与模拟值吻合得较好，从而验证了本文所建立的拱顶罐非稳态传热传质理论模型和计算方法的准确性。

3 实例应用与分析

本文利用上述模拟方法，以江苏省常州地区某液位为2 875 mm的1 000 m3拱顶汽油罐为研究对象，对该拱顶罐在春分日6∶00～18∶00时间段储罐内油品的蒸发损耗过程进行了数值模拟，分析了储罐内气相、罐顶、气体空间罐壁和液体空间罐壁温度、传热系数和液相蒸发量，并估算了储罐的小呼吸损耗量。该拱顶储罐数、汽油物性参数和外界环境条件见表2。其中，储罐内平均油品温度一天之内变化幅度不大，一般仅为1～3℃，因此假定罐内油品温度在春分日6∶00～18∶00时间段内上升2℃[19]。

表2 某拱顶储罐、汽油物性参数和外界环境条件Table 2 Basic parameters of a dome-roof tank,gasoline physical properties and external environmental conditions

3.1 储罐温度的变化规律

储罐温度主要受太阳辐射和大气环境温度的影响而发生变化。在早上6∶00时大气环境温度近似等于昼夜间最低大气温度，最高大气温度一般出现在中午12∶00～14∶00。同时，在中午时，由于太阳高度角最大，太阳辐射经过的大气行程最短，受到的削弱也最小，到达地面的太阳辐射量也最多，储罐吸收的太阳辐射量也最多，所以储罐温度也最高。图6为储罐内气相、罐顶、罐壁温度和大气环境温度随时间的变化趋势图。

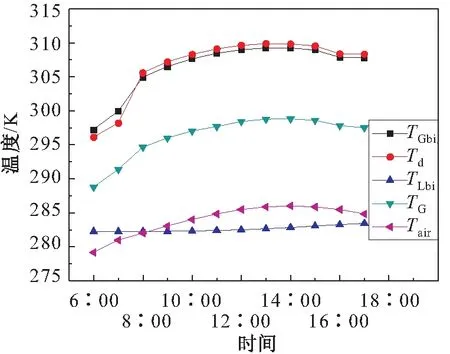
图6 储罐内气相、罐顶、罐壁温度和大气环境温度随 时间的变化趋势图Fig.6 Change curves of the temperature of gas phase, tank top,tank wall and the atmospheric environment with time 注：TG、Td、TGbi、TLbi、Tair分别为储罐内气相、罐顶、气体空间罐壁、液体空间罐壁和大气环境的温度。

由图6可见，储罐内气相、罐顶、气体空间罐壁和液体空间罐壁温度的变化趋势与大气环境温度的变化趋势一致，呈先升高后降低，最高温度出现在14∶00；由于气相比热容较小，其升温最快，单位热流量下的温升最大；由于液相温度较低且变化不大，故液体空间罐壁温度小于气体空间罐壁和罐顶的温度且变化不大；气相温度居于储罐边界(罐壁和罐顶)的温度和大气温度之间。

3.2 储罐传热系数的变化规律

图7为储罐内气相、罐顶、罐壁自然对流换热系数随时间的变化趋势图。

图7 储罐内气相、罐顶、罐壁自然对流换热系数 随时间的变化趋势图Fig.7 Change curves of the natural convection heat transfer coefficient of gas phase,tank top, tank wall with time 注：aG、aL、ad分别为储罐内气相与罐壁间、液相与罐壁间、气相与罐顶间的自然对流换热系数。

由图7可见，储罐内气相与罐壁间和气相与罐顶间的自然对流换热系数的变化波动很小，液相与罐壁间的自然对流换热系数的变化波动较大。这是由于自然对流换热系数与介质的密度、导热系数、运动黏度、比热容和温差有关，很显然液相与气相相比更易传热，因此液相与罐壁间的自然对流换热系数大于气相与罐壁、罐顶间的自然对流换热系数；又由于罐壁纵向自然对流强度大于罐顶横向自然对流强度，所以气相与罐壁间的自然对流换热系数大于气相与罐顶间的自然对流换热系数。根据模拟结果可知，储罐内气相与罐顶间自然对流换热系数的变化范围为1.40～1.61 W/(m2·K)，气相与罐壁间自然对流换热系数的变化范围为1.64～2.10 W/(m2·K)，液相与罐壁间自然对流换热系数的变化范围为31.05～73.05 W/(m2·K)。

图8为储罐内气相、罐顶、罐壁辐射换热系数随时间的变化趋势图。

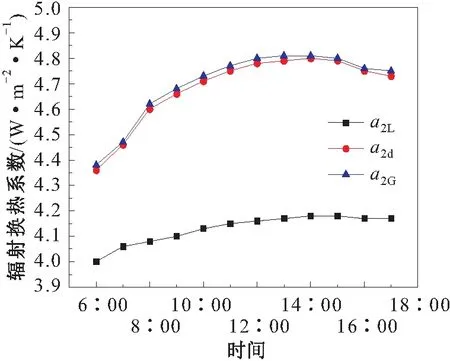
图8 储罐内气相、罐顶、罐壁辐射换热系数随时间的 变化趋势图Fig.8 Change curves of the radiation heat transfer coefficient of gas phase,tank top,tank wall with time 注：a2L、a2d、a2G分别为液体空间罐壁、罐顶、气体空间罐壁的辐射换热系数。

由图8可见，储罐内罐顶、气体空间罐壁和液体空间罐壁的辐射换热系数变化趋势一致，变化幅度也都不大。这是由于储罐边界黑度恒定，辐射换热系数的大小主要取决于储罐边界与大气环境之间的温差，由图6可明显看出，气体空间罐壁与大气环境之间的温差最大，罐顶次之，液体空间罐壁最小，因此气体空间罐壁的辐射换热系数最大，罐顶次之，液体空间罐壁最小；同时中午时分储罐边界与大气环境之间的温差较大，所以中午时储罐边界的辐射换热系数最大。根据模拟结果可知，储罐内罐顶的辐射换热系数变化范围为4.46～4.80 W/(m2·K)，气体空间罐壁的辐射换热系数变化范围为4.47～4.81 W/(m2·K)，液体空间罐壁的辐射换热系数变化范围为4.06～4.18 W/(m2·K)。

储罐边界的总传热系数由自然对流换热系数、辐射换热系数、强制对流换热系数、储罐边界的厚度和导热率决定。假设模拟的环境风速为定值(4 m/s)，则储罐内罐顶、罐壁的强制对流换热系数也为定值。储罐内罐壁的强制对流换热系数近似于空气横掠单管时的换热系数，罐顶的强制对流换热系数近似于空气掠过平板时的换热系数，分别为2.30 W/(m2·K)和7.70 W/(m2·K)。储罐边界的厚度很小而导热率又非常大，所以可忽略罐壁和罐顶的热阻。因此，根据模拟可得到储罐边界的总传热系数，具体见表3。

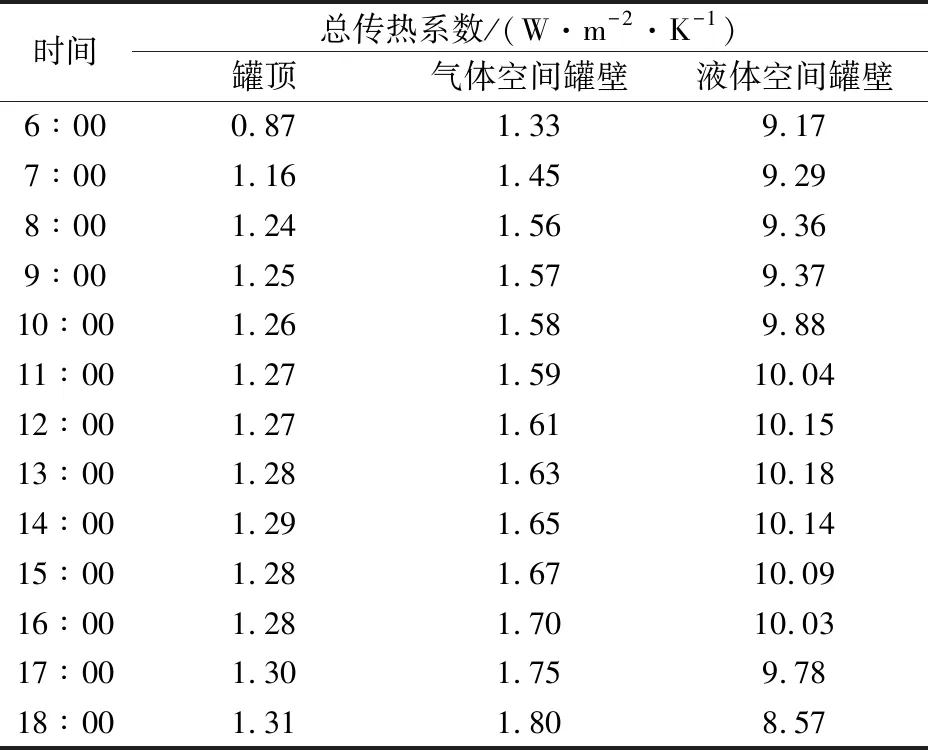
表3 储罐边界的总传热系数Table 3 Total heat transfer coefficient of the storage tank boundary

由表3可知，储罐内液体空间罐壁的总传热系数最大，其变化范围为8.57～10.18 W/(m2·K)，气体空间罐壁的总传热系数次之，其变化范围为1.45～1.80 W/(m2·K)，罐顶的总传热系数最小，变化范围为1.16～1.31 W/(m2·K)。

3.3 罐内液相蒸发量和气体膨胀量

储罐内液相蒸发量主要由液相的气化潜热、外界与液相以及气液两相间的传热量决定。储罐内液相蒸发量的模拟结果见图9。

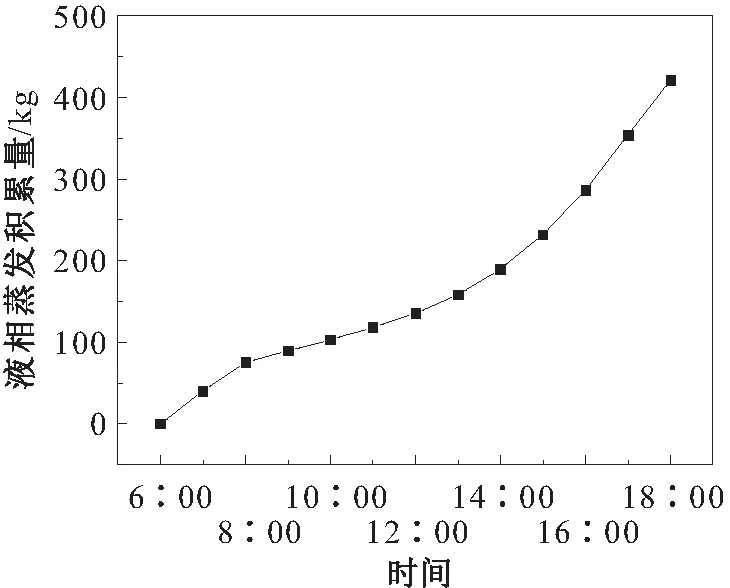
图9 储罐内液相蒸发累积量与时间的变化趋势图Fig.9 Change curves of the liquid phase evaporation accumulation of gas phase with time

由图9可见，在春分日6∶00～18∶00时间段内储罐内液相蒸发累积量逐渐增高，但其增加速率在早晨和下午时较大，中午时较小，这主要是由于早晨和下午时，太阳辐射主要集中于罐壁，液相吸收的太阳辐射热流量较多，有利于液相的蒸发，其蒸发量较大，而中午时，太阳辐射主要集中于罐顶，太阳辐射热流量自罐顶向下传递，由于气相热阻较大，不利于传热，故液相的蒸发量较小；在初始时刻蒸发量为0的条件下，在春分日6∶00～18∶00时间段内，液位为2 875 mm的1 000 m3拱顶罐内液相蒸发累积量为421.13 kg。已知罐内气体空间体积为850 m3，假设没有油气逸入外界环境，则罐内平均油气浓度为495.45 g/m3。另外，夜晚时，由于大气环境温度降低，且无太阳辐射，储罐开始向外界大气散热，罐内油气冷凝，液相蒸发量会减少。

根据式(14)和式(15)可计算得到气相温升引起的气体累积体积膨胀量Vh1为56.62 m3，逸入气体空间的油气所引起的气体体积膨胀累积量Vh2为157.44 m3，气体体积总膨胀累积量Vh为214.06 m3。图10为储罐内气体体积膨胀量随时间的变化趋势图。

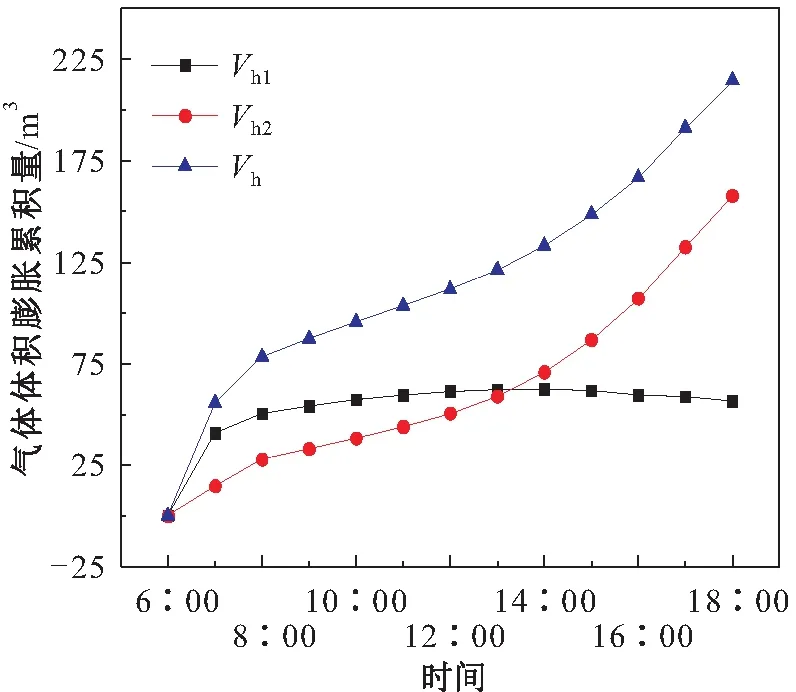
图10 储罐内气体体积膨胀累积量随时间的变化 趋势图Fig.10 Change curves of the sum of gas volume expansion accumulation with time 注：Vh1、Vh2、Vh分别为气相温升引起的气体体积膨胀量、油气逸入气体空间引起的气体体积膨胀量、油罐呼出的混合气体积。

由图10可见，Vh1主要受气相温升的影响，Vh1与气相温度变化趋势一致。在早晨6∶00至7∶00时间段，由于气相温升最大，此时的Vh1增加速率也最大，随后气相温度缓慢上升，Vh1也随之缓慢增加，在中午14∶00时气相温度达到最高值，Vh1也达到最高值，14∶00之后，气相温度逐渐降低，Vh1也随之逐渐降低。Vh2主要受液相蒸发量的影响，气体体积膨胀累积量与液相蒸发累积量的变化趋势一致。在早晨和下午时，液相蒸发速率较快，气体体积膨胀累积量的增加速率也较快，在中午时，液相蒸发速率较慢，气体体积膨胀累积量增加速率也较慢。

3.4 储罐小呼吸损耗量分析

由于夜晚期间储罐不再吸收太阳辐射，储罐向外界传热，因此可认为夜晚储罐的小呼吸损耗量为0，白天储罐的小呼吸损耗量即为储罐全天的小呼吸损耗量，为421.13 kg。另一方面，本模型很难得到罐内呼出的混合气体浓度，且其浓度必小于罐内平均浓度，罐内气体空间体积为850 m3，假设没有油气逸入外界环境，则罐内平均油气浓度由c=Δm/V计算得到为495.45 g/m3；为此，可假设呼出的混合气体油气浓度分别为50 g/m3、100 g/m3、200 g/m3、250 g/m3、300 g/m3、400 g/m3，进而计算出储罐相应的小呼吸损耗量，并与由公式(17)(美国API公式)计算得到的储罐小呼吸损耗量进行比较[20]。美国API公式如下：

(17)

式中:ΔmAPI为固定顶罐一天的小呼吸损耗量(kg)；PA为油品本体温度下的蒸汽压(kPa)，取32 kPa；Pa为大气压(kPa)，取100 kPa；ρL为液相密度(kg/m3)；D为油罐直径(m)；H为气体空间高度(m)；ΔT为大气环境温度的平均日温差(K)；FP为涂漆系数，取1；C为小罐修正系数，取1；K1为单位换算系数，取1；K2油品系数，取1。

基于API公式和体积-浓度法计算得到的储罐小呼吸损耗量见表4。

表4 基于API公式与体积-浓度法计算得到的储罐小呼吸损耗量对比Table 4 Comparison of calculated breathing losses of the storage tank between API equation and volume-concentration method

由表4可知，API公式计算得到的储罐小呼吸损耗量为50.84 kg，通过对比发现假设该模型罐内呼出混合气体油气浓度为250 g/m3时，基于体积-浓度法计算得到的储罐小呼吸损耗量为53.50 kg，此时两者是最为接近的。因此可以推断出该模型的呼出混合气体油气浓度大约为250 g/m3时，储罐小呼吸损耗量大约为50 kg，日损耗率约为0.23‰，降低储罐的小呼吸损耗是必要的，可选用储罐涂料等方法降低罐内温差，同时为响应国家“可持续性发展”的政策，各罐区应尽量进行油气回收。

4 结 论

本文基于变物性模型，建立了拱顶罐的非稳态传热传质理论模型，自编Matlab程序并通过自行搭建的实验平台验证其可行性，并以江苏省常州市地区某液位为2 875 mm的1 000 m3拱顶汽油罐为研究对象，研究在春分日6∶00～18∶00时间段内，储罐的温度、传热系数、液相蒸发量随时间变化的规律，估算了储罐的小呼吸损耗量，得到如下结论：

(1) 储罐内气相、罐顶和气体空间罐壁温度的变化趋势与大气环境温度的变化趋势一致，最大值均出现于14∶00左右；液体空间罐壁温度最低且变化幅度很小；气体空间罐壁和罐顶的温度非常接近，前者温度高于后者温度；气相温度居于储罐边界(气体空间罐壁和罐顶)温度和大气环境温度之间。

(2) 储罐内气相与罐壁、罐顶间的自然对流换热系数波动很小，而液相与罐壁间的自然对流换热系数波动较大；罐壁与液相间的自然对流换热系数最大，罐壁与气相间次之，罐顶与气相间的最小。辐射换热系数中储罐内罐顶、气体空间罐壁和液体空间罐壁的辐射换热系数变化趋势一致，变化幅度和数值大小相差不大；储罐内气体空间罐壁的辐射换热系数最大，罐顶次之，液体空间罐壁最小。总传热系数中与液相接触的罐壁的总传热系数最大，与气相接触的罐壁的次之，罐顶的最小。

(3) 储罐内油气浓度为0的初始条件下，液相蒸发量为421.13 kg；气相温升引起的气体体积膨胀累积量为56.62 m3，逸入气体空间的油气所引起的气体体积膨胀累积量为157.44 m3，总气体体积膨胀量为214.06 m3。假设呼出混合气体油气浓度分别为50 g/m3、100 g/m3、200 g/m3、250 g/m3、300 g/m3、400 g/m3,则通过体积、浓度法计算得到的储罐小呼吸损耗量分别为10.70 kg、21.41 kg、42.81 kg、53.50 kg、64.23 kg、85.60 kg。将其与美国API公式进行比较，得出该模型呼出混合气体油气浓度大约为250 g/m3，小呼吸损耗量大约为50 kg。