基于Gaussian Copula的木结构古建筑多准则地震易损性分析

郇君虹，马东辉，王 威，王子毅

(1.北京工业大学抗震减灾研究所，北京 100124；2.木结构古建筑安全评估与灾害风险控制国家文物局重点科研基地，北京 100124)

许多木结构古建筑因其具有的历史价值、艺术价值和文化价值等被列为文化遗产. 然而这些宝贵的文化遗产在地震中屡遭破坏，甚至倒塌，造成极大的经济和文化损失[1-3]. 因此，对木结构古建筑进行地震易损性分析是十分必要的.

地震易损性分析从概率的角度，对建筑结构的抗震性能进行定量描述，已经被广泛应用于建筑结构的抗震分析中[4-6]. Kouris等[7]等建立传统木结构建筑的简化模型，并对其进行非线性分析，建立结构的易损性曲线，发现传统木结构建筑具有很好的变形能力和抗震能力. Faye等[8]对传统木结构框架墙进行非线性频谱分析获得易损性曲线，发现其受力性能良好. Naveed等[9]对3个传统木框架砖石结构进行易损性分析，认为该种结构能够在地震峰值加速度(peak ground acceleration,PGA)小于0.7g的地区应用. 这些研究方法通常以层间位移角作为地震需求参数建立结构的易损性曲线，从单一的失效模式评估结构的易损性. 然而，木结构古建筑构造和材性复杂[10]，可以选用不同的地震参数[11]来评价其地震反应，因此其失效模式往往并不单一. 而且，建筑材料之间的相关性和相同的地震源会导致不同的失效模式之间具有非线性相关性. 因此在对木结构古建筑进行易损性分析时考虑不同失效模式间的相关性对其易损性的影响是十分必要的.

Sklar[12]于1959年提出的Copula理论能够很好地描述不同失效模式间的线性与非线性相关性. Copula理论已经广泛地应用于金融[13]、水文[14]和土木工程领域[15-16]. 鉴于此，本文提出基于Gaussian Copula函数、t Copula函数和Frank Copula函数[17]，考虑不同失效模式相关性的传统木结构古建筑易损性分析模型，并将该模型应用于某木结构古建筑的易损性评估中，为实际工程提供参考.

1 木结构古建筑地震易损性概率模型

木结构古建筑的地震易损性指不同强度地震作用下，木结构古建筑发生不同破坏状态的概率. 木结构古建筑的地震易损性可定义为：结构的地震需求Sr超过其延性能力Sn的概率[18].

Pf=Pr(Sn/Sr≤1)

(1)

在结构易损性分析中，一般认为Sn和地震动参数关系为

(2)

对式(2)取对数为

(3)

则失效概率为

(4)

通过式(4)可获得结构在各失效模式下的易损性曲线. 由于各失效模式之间具有相关性，本文引入Copula函数，考虑其对结构易损性的影响.

2 基于Copula函数考虑不同失效模式相关性的木结构古建筑易损性分析模型

2.1 Copula函数

Copula函数可以把随机变量X1，X2，…，XN的联合分布函数F(x1，x2，…，xN)与各自的边缘分布函数Fx1(x1)，Fx2(x2)，…，FxN(xN)关联起来. 若边缘分布函数Fxi(xi)(i=1，2，…，N)连续，则存在Copula函数C(x1，x2，…，xN)使得

F(x1,x2,…,xN)=

C[Fx1(x1),Fx2(x2),…,FxN(xN)]

(5)

Copula函数有很多种. 比较常用的Copula函数有t Copula函数、Gaussian Copula函数和Archimedean Copula函数等.

2.2 二维联合失效概率的Copula模型

二维Copula函数C(u,v)的定义域为[0,1]2，其边缘分布在定义域内服从均匀分布. 则联合分布函数为

F(x1,x2)=C(F1(x1),F2(x2);θ)=C(u,v;θ)

(6)

式中：u=F1(x1)与v=F2(x2)为边缘分布函数；θ为Copula函数的相关参数.

设x1和x2的边缘密度函数分别为f1(x1)和f2(x2)，则X1、X2的联合概率密度函数为

f(x1,x2)=f1(x2)·f2(x2)·c(F1(x1),F2(x2);θ)

(7)

c(F1(x1),F2(x2);θ)=∂2C(u,v;θ)/∂u∂v

(8)

由于Kendall秩相关系数可以反映出随机变量间的非线性相关性，因此本文采用Kendall秩相关系数来计算Copula函数的相关参数θ. 二维变量的Kendall秩相关系数τ与θ关系[17]为

(9)

假设在二维串联体系中，传统木结构古建筑各个失效模式所对应的功能函数为g1和g2，则二维串联体系中2个失效模式同时发生的概率为

P[g1(X)≤0，g2(X)≤0]=C(Pf1,Pf2)

(10)

从而可以得出二维串联体系的失效概率为

Pfs=P[g1(X)≤0∪g2(X)≤0]]=
P(g1(X)≤0)+P(g1(X)≤0)-
P[g1(X)≤0,g2(X)≤0]=
Pf1+Pf2-C(Pf1,Pf2)

(11)

式中Pf1、Pf2分别为二维串联体系中木结构古建筑2个失效模式的失效概率.

一般常用来计算结构易损性的Copula函数为t Copula函数、Gaussian Copula函数和Archimedean Copula函数中的Frank Copula函数. 二维情况下，3种函数的表达式为

二维t Copula函数

Ct(u,v;θ,k)=

(12)

二维Gaussian Copula函数

CG(u,v)=

(13)

二维Frank Copula函数

(14)

3 分析流程

本文提出木结构古建筑易损性曲线的建立方法，通过Copula函数考虑不同失效模式相关性对结构易损性的影响，完成对木结构古建筑易损性分析. 其具体分析步骤为：

1) 选取不同的地震需求参数，采用增量动力时程分析法建立结构在不同失效模式下的地震易损性曲线.

2) 通过式(9)计算地震需求参数间的相关系数θ.

3) 计算Copula函数的密度函数,根据式(11)～(14)得出考虑失效模式相关性的易损性曲线.

4 实例分析

4.1 木结构古建筑概况

以北京市东城区崇文门的花市火神庙为研究对象，建立考虑失效模式相关性的易损性曲线. 花市火神庙始建于明代，距今已有450 a历史. 花市火神庙在使用过程中曾遭损坏，于清代乾隆年间重新修缮，2004年又对其进行整体修缮. 花市火神庙建筑总面积为543.44 m2，其中后殿建筑面积为132.20 m2，主体结构形式为地上1层抬梁式木构架，无地下室，屋顶形式为木屋架两面坡筒瓦硬山屋顶，檐头高为3.7 m，屋脊高为7.0 m，台基高为0.7 m. 建筑的细部尺寸详见《清工部工程做法则例图解》[20]. 立面图见图1，平面图见图2.

对火神庙后殿进行现场检测，检测结果表明该建筑木材无明显腐朽，但局部有油漆剥落和构建开裂的状况. 其建筑外观损伤情况见图3.

4.2 单一失效模式下的失效概率计算

4.2.1 增量动力分析

运用Ansys软件建立结构的有限元模型. 木结构古建筑中的柱与额枋所采用的榫卯方式具有半刚性的特点，即节点介于铰接与刚接之间相对于弯矩作用所产生的转动变形而言，节点由于轴力、剪力及扭矩所产生的轴向拉压变形、剪切变形及扭转变形较小，可以忽略不计. 因此，榫卯节点的力学模型可以用弹簧单元来模拟. 花市火神庙的木柱直接搁置在础石之上，所以结构仅能依靠柱与础石之间的摩擦力来抵抗水平荷载，类似于铰接连接[21]. 基于此，采用杆系单元来模拟木结构古建筑的梁柱，用弹簧单元来模拟木结构古建筑榫卯节点的半刚性特点，柱底与地面采用铰接的方式. 采用壳单元来模拟屋盖. 根据古建筑屋面做法及恒活荷载组合[22-23]，计算所得屋面荷载为4 030 N/m2. 在建模分析时，结合建筑物实际残损状和相关文献[24]，对材料的力学性能进行了适当的折减，其简化计算模型如图4所示.

从太平洋地震工程研究中心强震记录库中随机选取100条地震波，来计算结构在不同地震波下地震的反应. 地震动可以通过PGA[25]、PGV[26]、Sa(T)[27]等强度指标来表示. 本文选取PGA作为地震动强度指标.

4.2.2 结构地震需求

木结构古建筑以木构架为主要承重体系，榫卯节点是构件间特有的连接方式. 历史震害资料[28]和相关实验研究并表明[29]，榫卯节点是木结构古建筑的抗震薄弱部位. 在地震发生时，木结构古建筑表现出小震下易损坏性和大震下的抗倒塌性. 小震下的易损坏性表现最为明显的部位为屋顶. 李铁英等[11]通过对应县木塔进行振动台实验研究，结合计算分析和震害资料，以变形、残损、构建承载能力及修复难易程度为基准，给出了震害等级和结构层间位移角(Δ/H)之间的关系，见表1. 榫卯节点是木结构古建筑主要承重体系的重要连接部位，也是薄弱部位. 半刚性的特点允许榫卯节点可以在一定范围内转动但转动范围有限. 而且随着转动角度的增大，节点残损及拔榫量会不断加剧. 根据《木结构古建筑维护与加固技术规范》[23]和张富文等[30]、Keita等[29]试验研究结果，总结分析几种常用榫卯节点转动角度(θ)和残损度之间的关系. 选取榫卯节点转动角度的余弦值(cosθ)作为衡量指标，该值和结构震害之间的对应关系见表1.

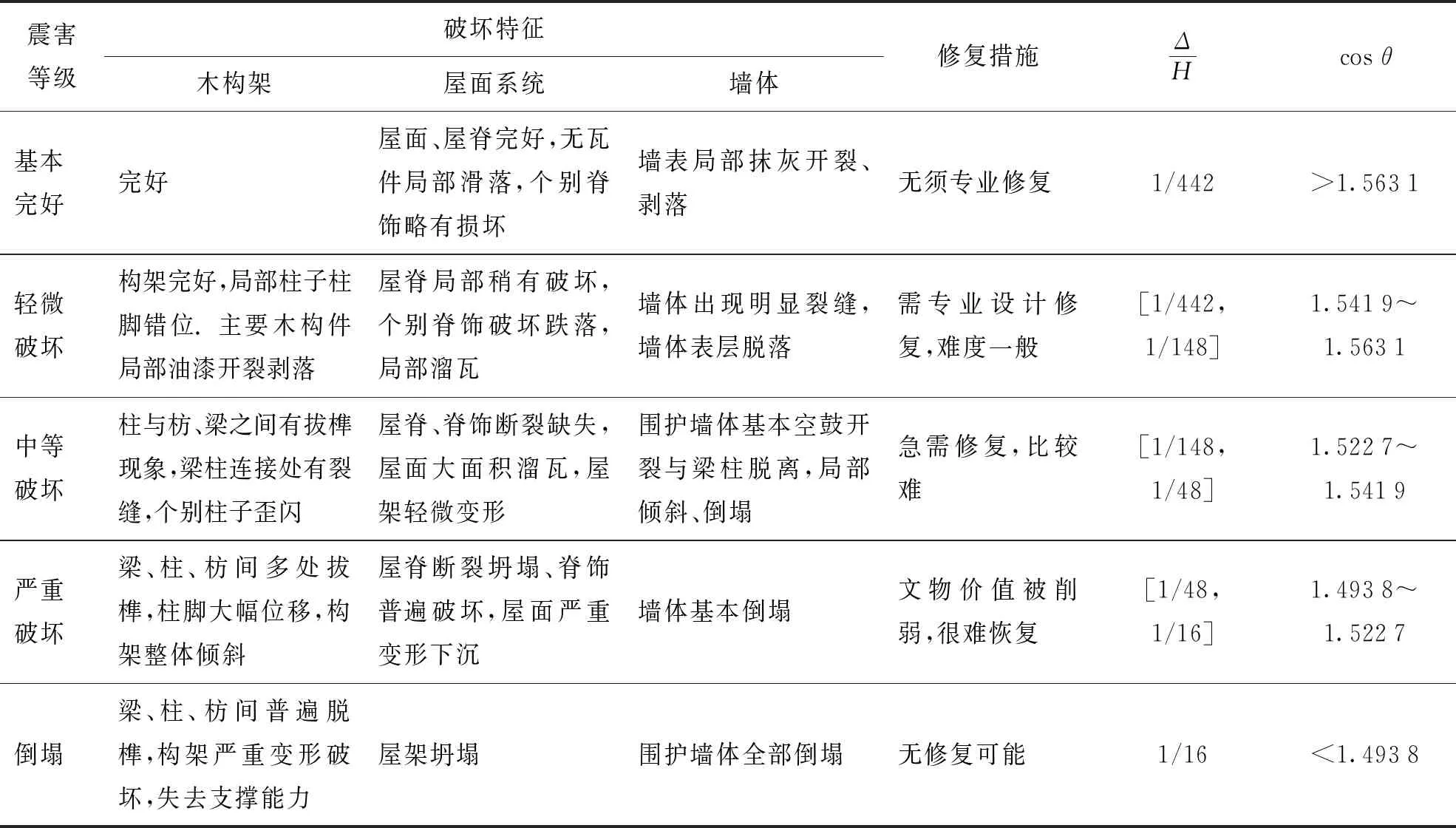
表1 花市火神庙极限破坏状态

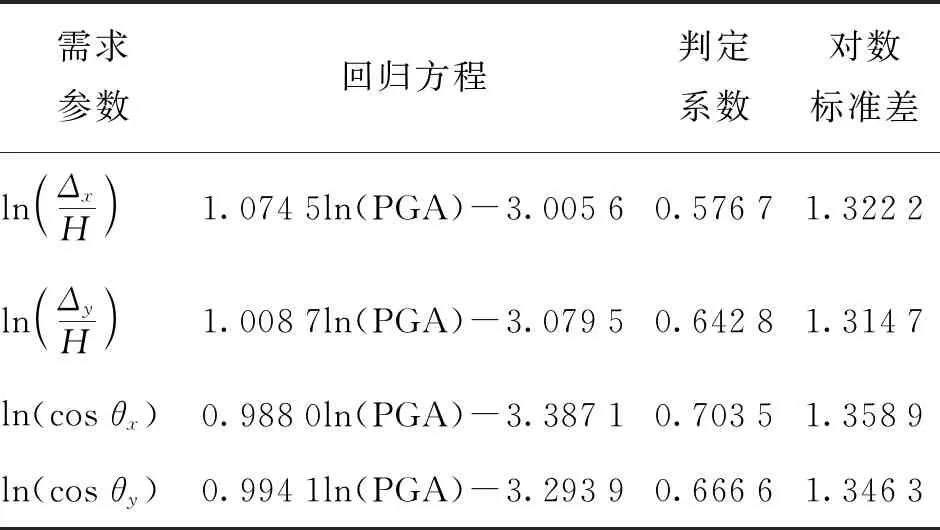
表2 木结构古建筑构件地震需求模型

4.3 考虑失效模式相关性的地震易损性分析

4.3.1 选取适当的Copula函数

根据各个需求参数的失效功能函数绘制二元频率直方图，根据直方图的特点，来选定适宜的Copula函数. 根据图7可知，该频率直方图具有对称的尾部，可以选取Gaussian Copula函数来描述各失效模式之间的相关性.

4.3.2 计算相关系数

根据式(9)对地震参数进行相关性分析得到结构地震需求之间的相关系数，见表3. 表3是通过Gaussian Copula函数计算所得的地震需求相关系数，相关系数的值小于1且均大于0.8，可以看出各地震相关参数之间是非线性相关的关系，其相关效果较为显著.

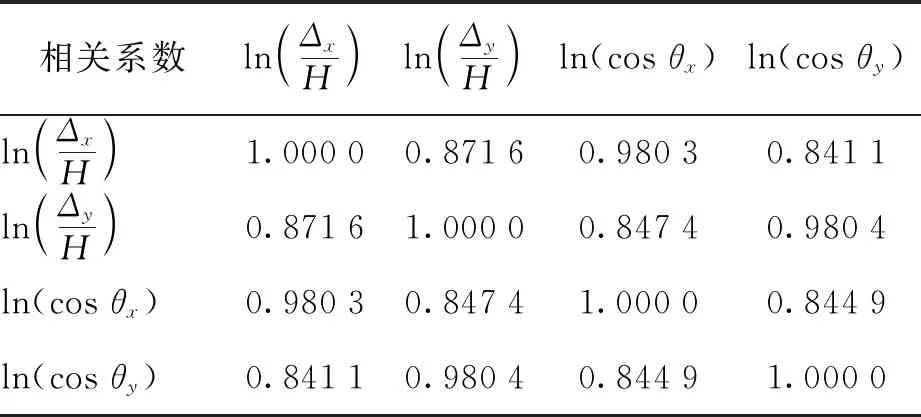
表3 结构地震需求之间相关系数

4.3.3 考虑失效模式相关性的破坏概率

运用式(11)～(12)计算花市火神庙后殿考虑不同失效模式间相关性的结构易损性曲线. 为了便于比较和表达，将Copula函数计算所得的易损性曲线绘于图6中.

通过对比发现，在4种破坏状态下，通过Gaussian Copula函数计算所得的失效概率大于任何一个失效模式的失效概率. 随着地震动强度的增加，考虑失效模式相关性的易损性曲线与单一失效模式的易损性曲线差距逐渐增大. 因此当地震动强度较大时，仅采用单一失效模式来衡量木结构古建筑的易损性时，可能会低估结构的抗震能力.

4.3.4 一阶界限法

为了验证Gaussian Copula函数的准确性，采用一阶界限法绘制结构的易损性曲线进行对比. 计算公式为

(15)

式中：Pi为构件i的失效概率；m为构件数量. 将构架易损性函数带入式(15)即可得结构易损性的上、下边界，见图6.

根据图6可知Gaussian Copula函数得到的结构易损性曲线介于上界和下界之间，并贴近于下界.

5 结论

1) 基于Ansys有限元软件及增量动力分析方法，建立了传统木结构古建筑的易损性模型. 将Copula函数应用于木结构古建筑易损性研究中. 选取明代建筑花市火神庙后殿为研究对象，根据地震需求参数的二维频率直方图具有对称尾部的特性，选取Gaussian Copula函数建立考虑失效模式相关性的传统木结构古建筑易损性曲线.

2) 考虑木结构古建筑失效模式相关性而得出的易损性计算结果要高于任何一种失效模式的易损性计算结果. 若以单一实效模式来衡量结构易损性，可能会低估结构易损性.

3) 运用一阶界限法建立花市火神庙的易损性曲线，并将计算结果与基于Copula函数计算得到的系统易损性曲线进行对比. 结果表明一阶界限法得到的木结构古建筑的易损性曲线有较大误差.