数字波束形成技术在现代雷达中的应用研究

2020-08-14徐其贵周继飞

无线互联科技 2020年10期

徐其贵，周继飞

（南京电子技术研究所，江苏南京 210039）

目前，雷达得到了广泛应用和快速发展。雷达最初主要是通过发射电磁波照射目标、接收回波这一方式来获得相关信息，如目标距离、速度等。后来，为满足现实需求，雷达需要具备更高的观测能力，如快速转换天线波束指向、发射高功率、高速跟踪多批目标等，相控阵雷达应运而生。数字波束形成则是在原来模拟波束形成原理的基础上，通过引入数字信号处理方法来建立的一种雷达新技术，其出现和发展是雷达技术与相关技术进步的产物，同时，还是现代电子战对雷达需要牵引的结果。自适应信号处理与阵列信号处理为数字波束形成技术的相关研究和实现提供了良好的方法与手段，同时，也为数字波束形成技术拓宽了应用领域[1-2]。

1 数字波束形成技术的发展及现状

随着集成电路、计算机等技术的发展，数字处理技术开始出现并逐渐应用到其他领域中。雷达的研究过程至今为止可以分为3个阶段，分别是早期、中期以及当前阶段。在初期阶段，主要是对雷达渐进行概念、理论层次上的研究；中期为关键技术研究阶段；当前是对试验系统的研究[3]。基于理论层次，在接收模式以及发射模式下形成的数字波束基本原理相同，所以，均可采用数字波束形成技术。数字处理技术具有许多模拟处理技术不具有的优点，在接收模式下具有一定的优越性，而因为当时存在技术方面的限制，对于其要求较低，因此，更加容易实现。研究对象在早期阶段为接收数字波束形成，而最早开始使用数字波束形成技术的是前西德的ELRA相控阵雷达，后来英、美、法以及我国都开始针对该技术开展相关研究。到了二十世纪七八十年代，一些工程实用的数字波束形成技术开始逐渐投入使用。到了20世纪90年代之后，各国都加大了对数字波束形成技术研究的投入，其发射模式下的数字波束形成技术性能也得到了提升，在一定程度上促进了数字波束形成技术应用在现代雷达信号处理领域中的范围扩大，为实现全数字阵列雷达奠定坚实的基础[4]。

2 数字多波束算法

2.1 均匀线阵接收信号模型

假设发射阵列是由M个全向阵元组成的，并且会呈现出均匀线性排列组合的形式，排列间距为d。利用这一阵列发射的窄带信号是，并且该复数的表达形式为：，如图1所示。

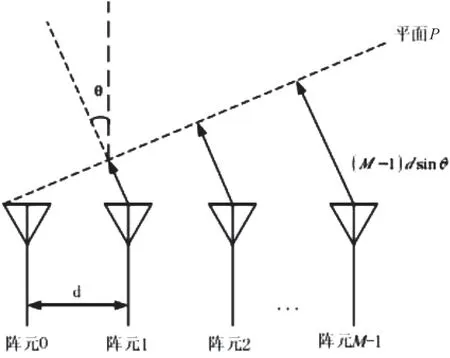
图1 均匀线阵发射信号模型

式中，ω0是发射信号的载波角频率，s（t）则是发射信号的复包络。对于方向为θ的远场接收区而言，如果未考虑电磁波空间传播是在逐渐衰减的前提这一条件，假设发射波是平面波P，将第一个阵元作为参考，如果信号是通过阵元1向着平面P发射，那么这一距离相较于阵元0来说，仅增加了一个dsinθ。通过阵元2发射平面P时，其距离增加另一个2dsinθ。通过阵元m发射，其距离多了mdsinθ。由电磁波传播的基本物理知识可以得知，信号通过阵元m发射，其时间会晚Tm，可以将其表示为

由于发射信号为窄带信号，s（t）属于慢变化，得到：

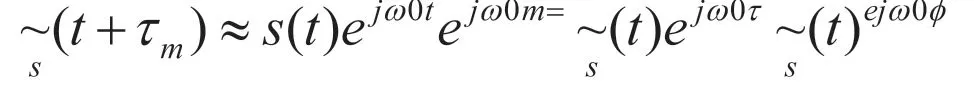
将整个发射阵列信号进行处理，可以写成向量形式，得出向量a（θ）是的方向矢量，其与发射角度、几何结构以及阵列位置之间具有直接关系。

2.2 数字波束形成基本原理

数字波束形成是在基带上利用数字方式来实现方向信号的接收，同时，将不需要的信号加以过滤。数字波束形成器与时域的横向滤波器的形成思路十分相似，还可以称之为空域滤波器。时域滤波器是通过控制抽头系数来进行滤波；空域滤波器通过控制权值进行滤波。这两种方式存在的差异为空域滤波器以方向划分信号，而时域滤波则以频率来划分信号。因此，只需要找到两种滤波之间的对应关系，就可以理解空域滤波器的原理。

2.3 发射数字多波束形成原理

基于叠加原理，通过推导发射数字波束形成原理可以得到发射数字多波束的形式。假设有L个信号向着θ1，θ2，…，θL方向发射，那么其发射的信号则是这一信号之和。发射多波束形成的输出信号可以表示为：，图2为该原理框架。

图2 发射同时多波束的原理

2.4 发射数字多波束形成的方法

2.4.1 数字配相的发射多波束算法

数字配相的发射多波束算法，即采用多组加权矢量在数字基带上分别对各个发射信号进行加权，并且每组加权矢量均会出现一个主瓣来指向特定方向。要想使波束的分辨率较高，就必须要对权向量的幅度进行改变，从而使波束形状得以改变。数字配相法具有发射多个波束的能力，并且其发射的波束具有任意指向，同时，还能够调整各个波束之间的距离，其波束在形状方面也存在一定的差异[5]。

实现数字配相法的方式十分简单，只要已知信号方向矩阵，就可以确定加权系数的值。由于各波束的指向非常独立，互补影响，理论上能够任意发射波束，但缺点是发射的信号如果均为同频信号、相关信号，那么实际的加权矢量为：。在发射同频信号的过程中，各个波束之间将会互相产生干扰，所以，在同频载波信号中不适合应用数字配相法。另外，如果未加窗，那么数字配相法形成的波束图旁瓣电平仅有-13.14 dB，而对于发射系统而言，如果旁瓣较大，将会消耗大量的发射功率。因此，为了抑制副瓣，可以采用加窗的方式，但是会导致主瓣变宽，从而对分辨方向角起到限制作用[6]。所以，在应用过程中，需要根据工程的实际需求，尽量采取折中的方法。

2.4.2 基于正交投影的发射多波束算法

基于正交投影的发射多波束算法的优势在于可以对发射角度进行随意调整。如果发射端的信号为已知状态，那么可以直接构造发射方向向量、需要指令的干扰子控件，并基于此对权值进行计算。如果干扰方向不是已知状态，则需要立即发射信号，与此同时，需要接收新方式，以此来获得干扰子空间，并对于其发射权值进行计算。通过正交投影算法来形成数字多波束的优势主要在于可以在任意方向上进行置零操作，所以，能够在其他发射波束的方向上置零，从而加大波束之间的隔离度，降低波束之间的叠加与干扰对多波束产生的影响[7]。

3 通道幅相不一致性分析

数字波束形成需要具备低副瓣、零点控制等优势，而阵列天线中的各通道需要具备一致性，并且通道之间需要保证传输无失真。在实际应用系统中，多通道之间难免会出现误差，导致算法实现结果与实际理论结果不符。因此，需要采取校正措施。通道校正是指将各个通道中存在的不一致性进行采集，然后利用校正信号来减小其对多波束发射产生的影响[8]。

3.1 通道幅相误差分析

数字波速形成系统的每一个阵元都拥有独一无二的信号通道，包括耦合器、混频、数模转换器（Digital to Analog Converter，DAC）以及功率放大器等，这些器件在材料、精度等方面存在差异，导致存在不同程度的抖动和噪声等问题，从而致使各通道之间在幅度以及相位响应方面出现误差，称为通道失配，还会导致波束旁瓣抬高，甚至出现无法形成波束的情况。

研究发现，幅相误差对波束图的影响和阵元数之间的联系十分紧密，为了方便分析，采用阵元数为16的均匀线阵[9]。但是各个通道的间隔幅相不一致性是时变过程，并且变化较为缓慢，因此，在具体场合的分析过程中，其特性可以视作不变。防震条件：阵元数为16，均匀线阵，阵元间距是半波长，期望的信号方向为[－20°，30°]，而干扰方向为[－40°，50°]，幅相误差范围为[－0.2，0.2]的均匀随机分布，相位则是[－0°，90°]的均匀随机分布。通过仿真实验结果可以得知，波束图主瓣与幅相误差之间存在漂移，而副瓣电平方向升高，同时，影响了干扰方向的抑制能力，致使波束性能下降。

3.2 不同算法下幅相不一致性特点

在幅度失真条件下和波束主瓣漂移中，横轴为幅度误差比例，纵轴为波束主瓣漂移绝对值的平均值[10]。波束图旁瓣电平会随着幅度误差的增加而逐渐上升，而另一种正交投影法所导致的旁瓣电平差明显低于数字配相法，但对旁瓣电平产生的影响十分相似。所以，在幅度误差相同的前提条件下，不同算法的失真表现也不同，而从旁瓣改变大小的角度对正交投影法进行考虑，其性能明显优于数字配相法，但是如果是基于实现校正的复杂度考虑，那么数字配相法相较于正交投影法更为简单。