《线性代数》支架式教学法初探

冷汹涛 吴集林 王柏清

摘 要：国家开放大学《线性代数》三大考核要点，求逆矩阵、线性方程组解的判定、求线性方程组的解，其解题过程中都以矩阵的初等行变换为关键手段，课堂教学中其固化解题步骤，为学生的学习搭建支架，引导学生对上述四个考核要点的知识进行自我构建，从而提高及格率。

关键词：初等行变换 固化解题步骤 搭建支架 自我构建 及格率

引言

国家开放大学《经济数学基础12》包含了《线性代数》和《微积分》两个部分[1]。在满分100分的期末考试的试卷中，《线性代数》占42分[2]。考核的知识点有矩阵的乘法、逆矩阵、矩阵的秩、线性方程组解的判定、线性方程组的解，有时两个或三个知识点结合在一道题目中考核，比如逆矩阵、矩阵的乘法、矩阵的加减法、单位矩阵、矩阵的转置相结合，矩阵的秩和线性方程组解的判定相结合。表1是试卷号为2006的期末试卷近三年《线性代数》分数的分布情况，表中“其他”主要包含矩阵的转置、单位矩阵、矩阵的加减法等。

从以上考分统计情况来看，求逆矩阵、线性方程组解的判定、求线性方程组的解是《线性代数》三大考核要点。其他考核知识点，如矩阵的加减法、矩阵的乘法、单位矩阵、矩阵的转置，所占分数较少，也容易掌握。

一、学情分析

“弯下腰捡支笔，直起腰再看老师的演算，已经两眼麻麻黑”——这是一名学生在班级微信里面描述的数学课，这句话从一个侧面说明了学生对数学课的畏惧心理。开放教育的学生，从学习态度、学习时间、学习方法、基础知识等几个方面，与普通高等教育的学生有着极大的差别[3]。学情归纳如表2所示。

特别说明一点，关于学生的“基础知识”，无论是业余班还是白天班，基础都很差[4] [5]。大部分同学10以内的正负整数的加减乘除不会算，分数的加减乘除不会算，他知道1-1=0，但“（-1）+1”他会等于2。

要把这样的学生教及格，是一件有难度的事情，走寻常路，实践证明行不通。

二、初等行变换

《线性代数》三大考核要点的解题方法如表3所示。

从表3可以看出，“初等行变换”是三大考核要点的关键解题手段。

初等行变换是对换变换、倍乘变换、倍加变换三种矩阵的行变换，基本意义分别如下：

对换变换：交换两行的位置，如图1所示。

倍乘变换：某行乘以一个常数k，如图2所示。

倍加变换：将矩阵的某一行遍乘一个常数后加到另一行，如图3所示。

这三种初等行变换的意义比较容易理解，学生也容易掌握。这是建构主义教学方法中支架式教学的第一步，明确搭建支架的材料。

三、固化解题步骤

教学过程中明确提出“固化解题步骤”，就是为学生的学习搭建支架。教师在例题演算过程中，严格按固化解题步骤解题，让学生明白构建知识的“脚手架”已经搭好。然后从易到难布置课堂训练题目，让学生顺着“脚手架”搭建自己的知识体系，教师在教室里巡回指点;与此同时任命能够迅速解出题目的学生为小组长，充当小老师，对不会的同学进行讲解，“先进带后进”，大家齐进步。

1.求逆矩阵

如图4所示，对左边矩阵A施行初等行变换，化为单位矩阵，右边的单位矩阵I化为A的逆矩阵A-1。

固化的解題步骤如表4所示。

2.线性方程组解的判定

线性方程组解的判定分两种情况，一种是非齐次线性方程组，即AX=b形式。其解题方法是对增广矩阵施行初等行变换，化为阶梯形矩阵，再根据课本上的定理3.1和定理3.2判定线性方程组的解。

另一种是齐次线性方程组，即AX=0形式。其解题方法是对系数矩阵施行初等行变换，化为阶梯形矩阵，再根据课本上的推论判定线性方程组的解。

从上述解题方法可以看出，对矩阵施行初等行变换，化为阶梯形矩阵是关键。阶梯形矩阵是形如图5的矩阵，其中表示某行的首非零元，×表示非零或零元素。

在教学实践中总结出的固化解题步骤如表5所示。

化成阶梯形矩阵后，其非零行的行数就是矩阵的秩（此处可解决求矩阵的秩这一考核要点），根据定理3.1和3.2以及推论就可判定线性方程组的解。

3.求线性方程组的解

求线性方程组的解分两种情况，一种是求解非齐次线性方程组的解，即AX=b形式。其解题方法是对增广矩阵施行初等行变换，化为行简化矩阵，再直接写出方程组的解。

另一种是求解齐次线性方程组，即AX=0形式。其解题方法是对系数矩阵施行初等行变换，化为行简化矩阵，再直接写出方程组的解。

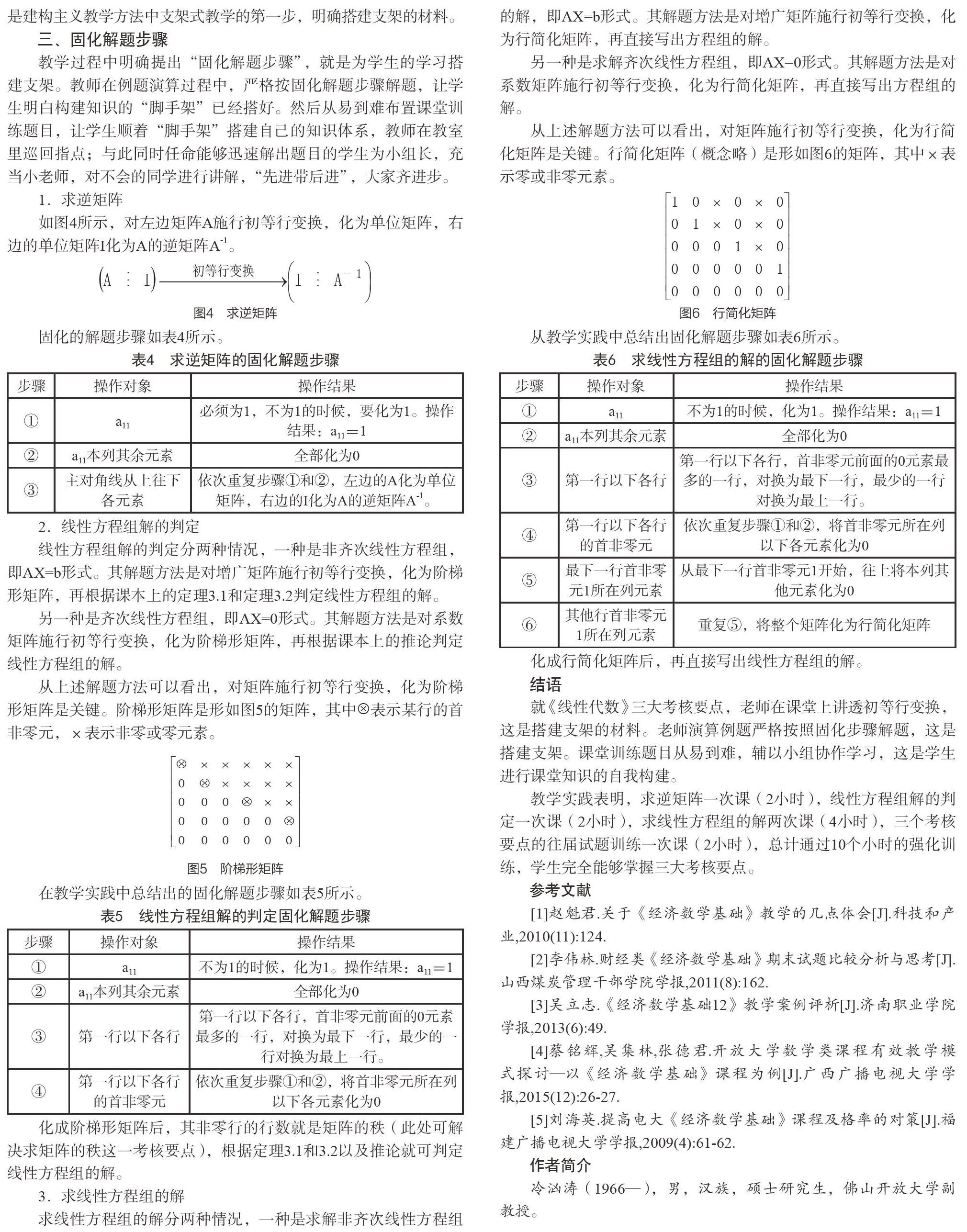
从上述解题方法可以看出，对矩阵施行初等行变换，化为行简化矩阵是关键。行简化矩阵（概念略）是形如图6的矩阵，其中×表示零或非零元素。

从教学实践中总结出固化解题步骤如表6所示。

结语

就《线性代数》三大考核要点，老师在课堂上讲透初等行变换，这是搭建支架的材料。老师演算例题严格按照固化步骤解题，这是搭建支架。课堂训练题目从易到难，辅以小组协作学习，这是学生进行课堂知识的自我构建。

教学实践表明，求逆矩阵一次课（2小时），线性方程组解的判定一次课（2小时），求线性方程组的解两次课（4小时），三个考核要点的往届试题训练一次课（2小时），总计通过10个小时的强化训练，学生完全能够掌握三大考核要点。

参考文献

[1]赵魁君.关于《经济数学基础》教学的几点体会[J].科技和产业，2010（11）：124.

[2]李伟林.财经类《经济数学基础》期末试题比较分析与思考[J].山西煤炭管理干部学院学报，2011（8）：162.

[3]吴立志.《经济数学基础12》教学案例评析[J].济南职业学院学报，2013（6）：49.

[4]蔡铭辉，吴集林，张德君.开放大学数学类课程有效教学模式探讨—以《经济数学基础》课程为例[J].广西广播电视大学学报，2015（12）：26-27.

[5]刘海英.提高电大《经济数学基础》课程及格率的对策[J].福建广播电视大学学报，2009（4）：61-62.

作者简介

冷汹涛（1966—），男，汉族，硕士研究生，佛山开放大学副教授。