案例驱动的“离散数学”教学研究

金耀 胡雅丽 田秋红 宋瑾钰

[摘 要] 针对“离散数学”课程概念多、理论性强、内容抽象，而学生不易掌握，更不会应用等现象，分析了离散数学在衔接自然语言与程序语言中所起的重要作用，以讲授“等价关系”知识点为例探讨了案例驱动的教学方法，以期培养并提高学生理解与运用数学知识的能力。

[关键词] 离散数学;数學思维;教学方法

[基金项目] 2017年度浙江理工大学课堂教学改革项目“《离散数学》案例式教学的研究与实践”（kg201707）;2019年度浙江理工大学教学改革项目“基于培养学生多元化能力的《离散数学》全英文课程的改革与完善”ylxm201908）;2017年度中国纺织工业联合会教育教学改革项目“以能力培养为核心的《Java程序设计》实验教学改革与实践”（2017BKJGLX293）

[作者简介] 金 耀（1984—），男，浙江绍兴人，工学博士，浙江理工大学数字媒体技术系讲师，硕士生导师，主要从事计算机图形学研究;胡雅丽（1986—），女，浙江绍兴人，机械工程硕士，浙江理工大学信息化办公室工程师（通信作者），主要从事高校数据治理与大数据分析研究;田秋红（1976—），女，辽宁兴城人，理工学博士，浙江理工大学信息学院副教授，硕士生导师，主要从事图像处理与模式识别研究。

[中图分类号] G642.0    [文献标识码] A    [文章编号] 1674-9324（2020）29-0264-03    [收稿日期]2019-09-20

一、引言

“离散数学”作为一门面向计算机类专业的数学课程，是该专业的一门重要基础课程，同时也是许多其他核心课程的先导课程[1]。因此，学好“离散数学”课程不仅对于计算机类专业的学生非常重要，而且也赋予了教师相应的使命感。

“离散数学”课程的特点是概念多、理论性强、内容抽象，因而学生想掌握该课程并非易事。笔者在教学与科研实践中发现不同阶段的学生对离散数学的认识均存在着偏见。不少低年级学生认为该课程难度大、听课累、兴趣不高;相当部分的高年级学生认为该课程没有实际用途，与专业相关性小;甚至有部分研究生也存在着类似的观点，其在解决问题时，往往绕过严密的数学推演而直接写代码，从而时常出现代码质量差、准确率低等问题，而究其原因往往是没有把问题想明白，即未曾用数学语言对问题进行严谨的定义与精确的建模。

“离散数学”所教授内容虽然以数学知识点为主，具有较强的理论性，但其计算机专业的属性又使其同时具有应用性的特点，因此适合案例教学，使学生更好地掌握理解与运用理论知识的技能。案例教学法即将教学案例引入课堂，引导学生以案例为基础对知识点进行理解、分析与思考[2]。不少教学工作者探索了面向“离散数学”课程的案例教学方法。其中一类探讨案例教学的方法论。闵勇以创新实践案例为基础，利用翻转课堂和创新项目的形式开展教学[3]。徐周波等人结合逆向案例，将教学设计思路“提出问题—分析问题—引入概念—抽象建模—设计分析—程序设计”贯穿于教学活动中[4]。另一类则注重具体案例的设计与实施。吴伟以计算机鼓轮设计为例，从问题的提出、分析与解决三阶段讨论了案例教学的实施过程[2]。徐周波等人以有序二叉决策图（OBDD）为例探讨了离散数学的应用场景[5]。陈光喜等人以“成语接龙”游戏为例分析了案例使用的思路、方法及其作用[6]。杨洪等人以若干经典应用案例为例从精选案例、科学设计讨论问题、讨论与总结等方面探索了案例教学方法[7]。贲可荣与谢茜针对解题中的应用案例，分析求解过程以此激发学生的学习兴趣[8]。

受到上述教学思路的启发，笔者亦尝试将案例式教学方法引入“离散数学”课程的教学。与上述方法所不同的是，本文从离散数学的“枢纽地位”出发，以“等价关系”为例剖析其在问题描述与求解中的关键作用，以期加深学生对离散数学概念与原理的理解，激发其学习兴趣，培养其数学思维，提高其分析和解决实际问题的能力，从而达到学以致用的目的。

二、离散数学的枢纽地位

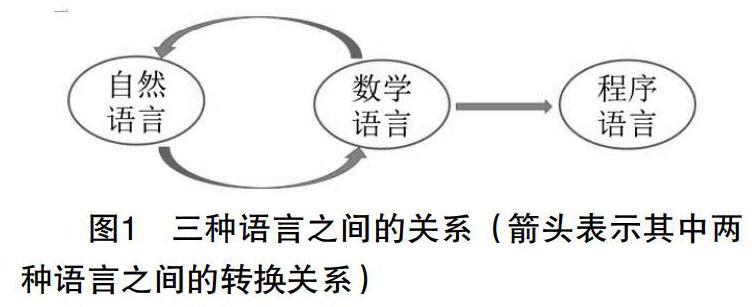
计算机类专业具有很强的实践性，以培养学生运用程序语言解决实际问题为目标。然而以自然语言描述的实际问题往往与程序语言存在“鸿沟”，往往难以运用程序语言直接描述与解决问题。而离散数学作为计算机的数学语言，扮演着衔接自然语言与程序语言的角色，起着上承自然语言，下启程序语言的枢纽作用。

图1所示即为三种语言之间的转换关系。一方面，数学语言虽精确严谨，但往往晦涩难懂，因而运用直观的自然语言表达数学语言有助于学生理解其背后的内涵;另一方面，数学语言能够将自然语言所表达的问题形式化与精确化，有助于运用所学的数学知识解决实际问题。此外，数学语言又与程序语言最为贴近，为程序设计提供直接的依据，有助于提高程序设计的效率与准确率。笔者尝试运用图1所述离散数学的枢纽作用作为指导思想，结合具体案例讲授离散数学课程知识，力求将知识点化难为易，同时强化学生以逻辑思维与计算思维为主的数学思维能力，为其今后的学习与研究打下扎实的基础。

三、案例教学之“等价关系”

（一）案例设计

作为教学案例，异于例题，其应具有趣味性、前沿性、综合性、多样性与可操作性等特点[3]，同时又能生动地体现图1所示内涵，反映了离散数学的枢纽地位。因此案例的设计对授课教师提出了较高的要求，促使教师在日常生活中细致观察与思考问题，并充分挖掘科研领域的资源，设计出理想的案例，以期达到科研反哺教学的目的。

在设计案例内容时，需深入思考、理解案例的本质，明确其在离散数学枢纽地位中扮演的角色，从而能够有效地将案例与知识点有机结合，深刻理解知识点的内涵与外延作用，在课堂讲授时能够清晰地呈现给学生。以下以“等价关系”这一离散数学中重要章节为例，讲述案例驱动的教学方法。

（二）等价关系的定义——几何变换

教材在介绍“等价关系”时，往往直接给出其数学定义——满足“自反、对称与传递”性质的关系。学生面对这一概念时，往往难以揣摩“等价”的含义，不明白为什么把具有这三种性质的关系定义成等价关系，而不得不通过死记硬背的方式把该知识点强记于心。对此，笔者设计了计算机图形学中几何变换的案例，借助自然语言解释该数学概念，将抽象的数学概念运用生活语言进行描述，并通过合理的课堂设计，引导学生自己思考、定义等价关系，使其更好地理解知识点，领悟教材未能言明的内涵。

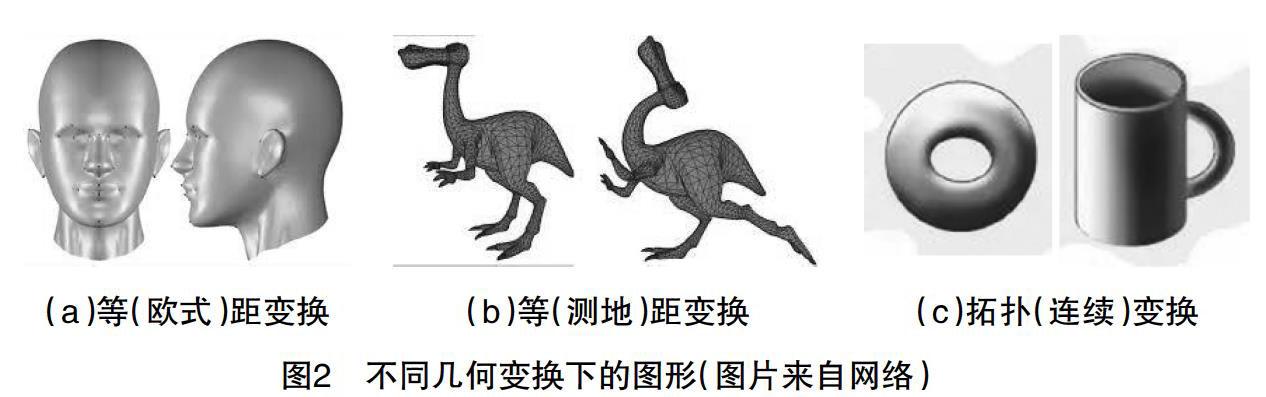
在讲授“等价关系”概念前，首先以图2所示的三组图形作为引子，对其进行逐一解释。其中（a）图表明在等欧式距离变换下两模型可看作同一个;（b）图表明在等测地线距离变换下两模型也可认为是相同的;（c）图表明在拓扑或连续变换下两模型也是等同的。三组图共同描述了几何对象在固定的变换下保持某种性质不变的现象。然而进行课堂讨论，对学生进行提问“若将几何变换是否是关系，若是则其满足哪些性质？”。经过讨论，学生不仅对等价关系有了直观的认识，而且据此可以自己给出等价关系的数学定义。进而学生通过该案例明白了一些观点：分类是人们认识事物规律的一种常用方法;而同一类事物采用“等价”这一概念进行描述;两个对象“等价”是相对的，即在某种关系下等价，而在另一种关系下可能不等价，等等。

通过该实例的讲解，学生不仅对等价关系有了直观的认识，而且据此可以自己给出等价关系的数学定义，并且后续即将学习的“等价类”与“商集”等概念也自然理解了。这种案例教学不仅调节了课堂气氛，而且激发学生的学习兴趣，使其更易掌握知识点，领会数学知识背后的思想与方法。

（三）等价关系的应用——图像分割

数学语言亦可刻画自然语言，能够准确地定义问题，理解问题的本质，进而方便问题的建模与求解。在教学中力求将离散数学知识点与应用案例的紧密结合，培养学生运用书本所学的知识点描述与解决实际问题。

笔者在讲授等价关系知识点以后，布置一个作业，即要求学生运用等价关系与集合划分的数学语言对数字图像处理的一个经典问题——“图像分割”下一个严格的数学定义。图像分割运用自然语言描述即把图像分成若干个特定的、具有独特性质的区域并提出感兴趣目标的技术和过程[9]，如图3所示，将（a）图中的表示不同对象的区域分离出来。

学生根据笔者给出的图像及分割的描述，从具体案例中思考图像与分割和集合与划分之间的联系，并尝试用集合划分的语言为其下定义。学生通过类比的方式，明白了图像分割是一种特殊的集合划分，既有集合划分的共性，也有其特殊性——同一等价类是一个连通域。

通过该练习，学生不仅加深了对集合划分概念的理解并了解了图像分割这一重要的图像处理问题，而且通过多次训练逐步学会如何運用数学思维思考问题，并掌握运用数学语言描述问题的方法。

（四）等价关系的实现——等价关系的判定

离散数学既具有理论性又具有实践性。为巩固离散数学的知识点，同时提升学生用程序解决实际问题的能力，笔者尝试开设少量的实验课，尝试将数学描述的概念与方法，运用程序语言加以实现。

笔者选取了一些难度相对较小又具有代表性的案例，如等价关系的判定，即给定用数学语言描述的关系R，据此判断R是否是等价关系。引导学生如何从关系的三种数学描述（集合法、关系矩阵、关系图）出发建立相应的数据结构，根据等价关系的三个性质设计出相应的算法，并最终通过编写程序实现。从而逐步培养学生用数学的眼光看待实际问题，用程序的思维看待数学问题，学会建立数学语言与程序语言内在的联系。

四、教学效果

笔者根据上述教学思路，设计了约50余个案例与大纲的一些重要或难度较大的知识点结合，并在“离散数学”课堂实施教学活动已有两年，取得了良好的教学效果。通过问卷调查了解到，超过93%的学生对课题教学满意或非常满意，近86%的学生认为案例对理解知识点帮助很大，超过88%的学生希望在今后的教学中也能增加案例。关于案例的内容与呈现方式，63%的学生对专业应用案例，如人工智能、图形图像处理等较为感兴趣，近84%的学生喜欢图片与视频形式的案例。上述数据表明，学生对课堂教学效果认可度较高。此外，从平时课堂测试以及期末成绩来看，大部分学生均能较好地掌握知识点，能够举一反三，并运用离散数学的理论知识解决一些实际问题。

五、结语

本文讨论了离散数学在衔接自然语言与程序语言起着重要的枢纽作用，以讲授“等价关系”知识点为例，探讨了“离散数学”课程的案例式教学方法。课堂实践表明，该教学方法不仅能够将教学内容化难为易，更好地传授知识点，而且能将理论与应用实践紧密结合，激发学生的学习兴趣，培养其数学思维能力，起到了良好的教学效果。

参考文献

[1]耿素云，屈婉玲，张立昴.离散数学（第五版）[M].北京：清华大学出版社，2013.

[2]吴伟.浅析离散数学课程中的案例教学法[J].科教论坛，2018（12）：42.

[3]闵勇.基于创新实践案例的离散数学教学方法[J].计算机教育，2016（16）：39-42.

[4]徐周波，古天龙，常亮.突显能力培养的离散数学逆向案例教学改革探索[J].计算机教育，2017（12）：69-72.

[5]徐周波，古天龙.“离散数学”中的OBDD案例教学研究[J].计算机教育，2010（2）：122-124.

[6]陈光喜，古天龙，常亮，等.一个“离散数学”课程教学案例的应用分析[J].工业和信息化教育，2018（4）：12-14.

[7]杨洪，张宏礼，朱桂英.离散数学课程案例式教学方法初探[J].计算机教育，2015（15）：27-30.

[8]贲可荣，谢茜.通过应用案例提高离散数学教学效果探究[J].软件导刊，2016，15（12）：35-37.

[9]Milan Sonka，Vadav Hhvac，Roger Boyle，et al.Image Processing，Analysis，and Machine Vision[M].北京：人民邮电出版社，2003.

[10]Lin D，Dai J，Jia J，et al.Scribblesup：Scribble-Supervised Convolutional Networks for Semantic Segmentation[C].Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition，2016：3159-3167.