一种改进的基因微阵列数据分类算法
2020-08-13马越刘成忠
马越 刘成忠


摘 要: 针对基因微阵列数据具有维数高、样本小、冗余高的特点,为了提高基因分类算法的性能,提出一种基于灰狼优化和支持向量机的分类算法。该算法使用主成分分析法进行数据降维,选取15个相关系数最大的基因探针,利用改进的灰狼优化算法对支持向量机的奖罚因子C与核宽度σ进行参数寻优,并在2组公开的癌症微阵列数据上进行试验。实验的准确率分别为95.24%和 94.00%,通过与其它算法进行性能对比,该算法具有高效、精准的分类能力,对临床医学应用有极为重要的参考意义。
关键词: 基因微阵列;基因分类;主成分分析法;支持向量机;灰狼优化算法
中图分类号: TP18 文献标识码: A DOI:10.3969/j.issn.1003-6970.2020.06.002
本文著录格式:马越,刘成忠. 一种改进的基因微阵列数据分类算法[J]. 软件,2020,41(06):0711+31
【Abstract】: In order to improve the performance of classification algorithm, a classification algorithm based on Grey Wolf Optimizer (GWO) and Support Vector Machine (SVM) is proposed for the high dimension, small sample and high redundancy of gene microarray data. In this algorithm, Principal Component Analysis (PCA) was used to select 15 gene probes with the largest correlation coefficient. Then, the improved gray Wolf optimization algorithm was used to optimize the parameters of reward and punishment factor C and kernel width of SVM, and two groups of cancer microarray data were tested. The accuracy of the experimental results was 95.24% and 94.00%, respectively. Compared with other algorithms, this algorithm has the ability of efficient and accurate classification, which is of great reference significance for clinical medicine application.
【Key words】: Gene microarray; Genetic classification; Principal component analysis; Support vector machine; Grey wolf optimization algorithm
0 引言
各種癌症及恶性肿瘤一直威胁着人类的生命健康,但是患病早期并不容易被查出,所以为各种疾病提供一种高效、准确的诊断方法,可以让患者及时接受治疗,或许可以挽救患者生命。随着基因微阵列技术的成熟,基因表达谱可以表示人类各个组织的正常基因,而且由于大量患者的贡献,很多重大疾病的基因微阵列数据也已经被共享,为基因分类与识别提供了大量的可靠数据。文献[1-4]众位支持向量机算法做了诸多研究,傅德胜[5]等人对PCA降维算法做了详细介绍和研究。文献[6-8]众位研究人员对癌症基因微阵列进行了特征选择,得到了低维可分的数据集。Chiaretti [9]等对白血病基因微阵列数据集的分类进行了研究,并应用到临床治疗和预测之中;Sun[10] 等在肺癌临床治疗中通过对肺癌微阵列数据特征分类从而做出预判;van t Veer LJ[11]等人对乳腺癌微阵列数据进行了特征分类与预测。文献[12-13]对灰狼算法进行了详细介绍。Xianhai Song[14]等人将灰狼优化算法(Grey Wolf Op-timizer,GWO)与重力搜索算法(GSA)、遗传算法(GA)、粒子群优化算法(PSOGSA)和梯度算法做了相关比较,指出了灰狼优化算法的鲁棒性较强且收敛速度极快,所以适用于优化支持向量机的奖罚因子C与核宽度。蔡立军[15]等人及叶明全[16]等人都使用蚁群算法对基因分类算法进行优化,准确率接近90%。陶国娇[17]提出了一种优化群智能算法的方法,可以提高算法寻优精度,赵乃刚[18]和曹盟盟[19]等人都对粒子群算法做了优化和改进,使得其优化能力得到了进一步提升。靳艳虹[20]做了基于粒子群算法的基因表达数据的研究,使用粒子群算法提升分类准确率,但是粒子群算法的收敛速度明显不如灰狼优化算法。本文首先使用PCA降维算法对数据集进行降维,然后使用基于改进灰狼优化算法的支持向量机做分类,提升支持向量机的分类效果。由于改进的灰狼优化算法相对于其他群智能算法,其收敛速度较快,所以在提高分类准确率的同时算法时间复杂度问题也有所改善。
1 主成分分析法
主成分分析法(PCA)是数据降维中最常见的线性方法,PCA的目的是从样本诸多属性值中找到并保留相关系数最大的属性值,从而达到降维效果。
将样本点xi投影到新空间超平面上,并且使得样本投影尽可能分开,此时就需要投影的方差最大化。
其主要步骤如下:
(1)计算样本对应的协方差矩阵 ,此时的协方差也可以看成相关系数;
(2)对矩阵XXT进行特征值分解;
(3)降序后取最大的D个特征值所对应的特征向量,即相关系数最大的属性对应的特征向量;
(4)輸出D维投影矩阵即目标矩阵可以用式(1)表示为:
2 支持向量机
经过数据处理,使用支持向量机可以对所选的两组数据集进行分类处理。支持向量机(SVM)结合了VC维理论和最小化结构风险,SVM分类的中主要依靠支持向量机,少数的支持向量决定了最后的结果,在剔除大量冗余样本属性的同时具有很好的鲁棒性,增加或删除非支持向量样本对模型没有影响,对于基因微阵列这种维度高,样本少的数据分类极为适用。
其主要思想是将样本通过核函数变换后从低维的不可分到高维的可分,找到一个超平面 将数据分成正样本和负样本两类。最好的分类结果为距离超平面H最近的正、负样本的距离最大,即目标函数为式(2):
支持向量机有两个重要参数 和C。如果 太大,高斯分布会变成细长型,只能作用于支持向量样本附近,造成支持向量机独立分类效果变差,而且容易发生过拟合。反之,如果 太小,高斯分布会变成矮宽型,此时曲线过于平滑,无法在训练集上取得较高的准确率。系数C被称为奖罚系数,C的值越高,说明此时支持向量机接受误差能力变差,容易发生过拟合,但C值太小又容易发生欠拟合现象,所以选取适合的系数C和 极其重要。
3 灰狼优化算法及改进
灰狼优化算法(GWO)最早是由澳大利亚的学者Mirjalili等人在2014年提出的。灰狼优化算法是在观察灰狼在狩猎过程中进行的一系列规律活动而受到启发,形成了一种新型的群智能优化算法,该算法具有很强的收敛性,还具有参数少等特点,可以被应用于图像分类,参数优化等领域.
GWO首先是种群等级划分。计算种群每个个体的适应度,并根据灰狼种群适应度不同,由高到低将其分为 。如图1所示。
狼是整个狼群的领导者,具有最高的适应度,是距离最优解最近的狼。其次是 狼,他们是仅次与头狼的等级,他们负责协助头狼领导狼群,同时也是头狼的候选,最后是 狼,主要是平衡狼群内务关系和协助前三种狼。
灰狼优化算法把狩猎过程分成包围,追捕及攻击三个步骤,目标为获取猎物,即得到全局最优解。算法实现如下:
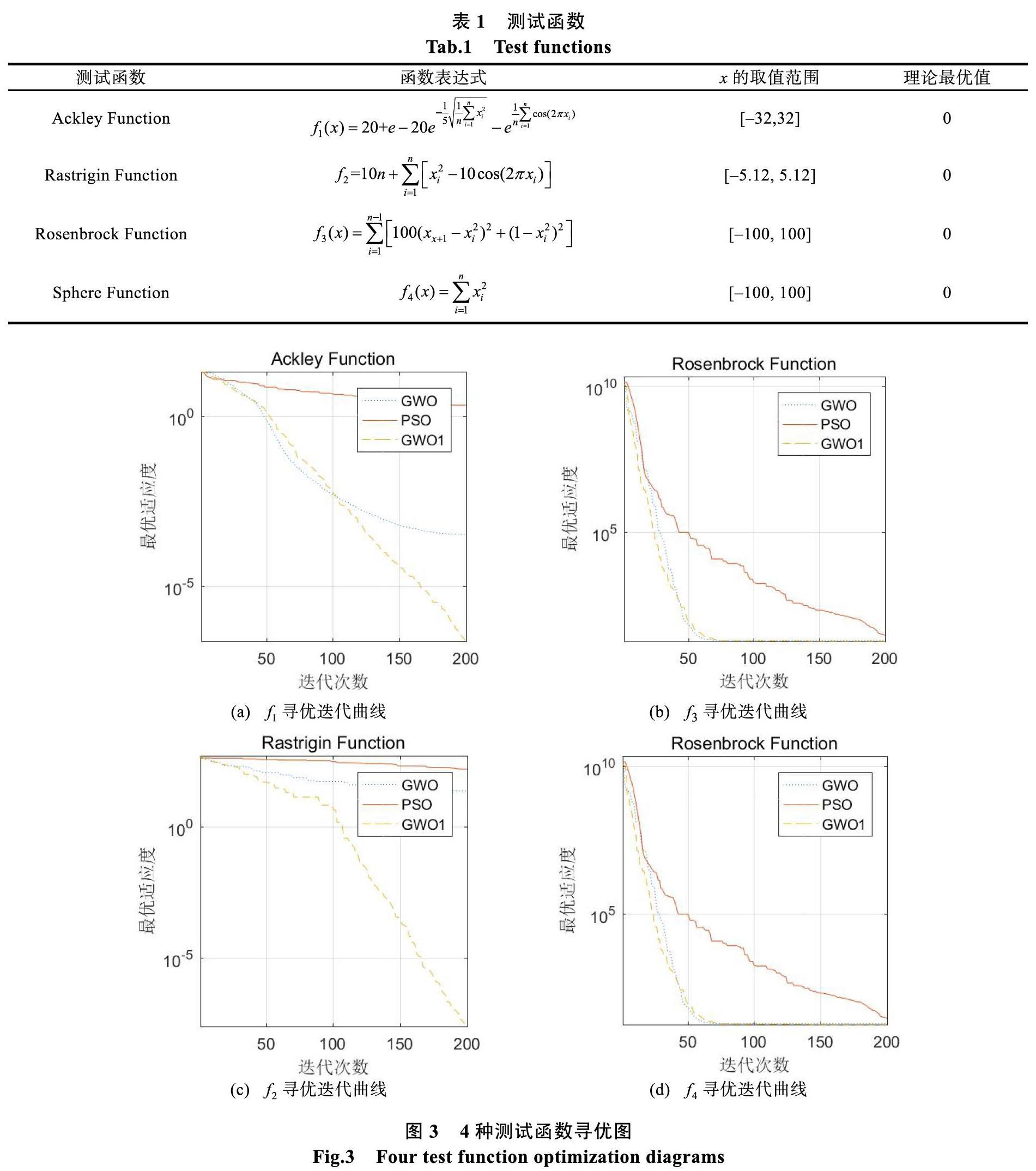
图3中直线,短虚线,长虚线分别为粒子群算法,传统灰狼优化算法,改进后灰狼优化算法最优适应度(最优解)变化曲线,显然,不管从收敛速率还是收敛精度来看,传统灰狼优化算法和改进后灰狼优化算法都明显优于粒子群算法。在算法前期,改进的灰狼优化算法相对于传统灰狼优化算法有优势但不明显,算法后期改进后的灰狼算法在测试函数的测试下,无论从下降速率(收敛精度)还是从最优适应度(收敛精度)来看都具有明显优势,所以此次对灰狼算法的优化是极有意义的。
4 仿真实验
4.1 数据集及实验环境
本文使用的数据集I为多发性骨肿瘤样本,包括173个样本,通过Affymetrix U95Av2微阵列获得122625个基因的表达谱。保存在美国生物技术信息中心(http://www.ncbi.nlm.nih.gov/geo/)编号GSE755。使用的数据集Ⅱ为肺癌样本,包括181个样本,cRNA与人类U95A寡核苷酸探针阵列(Affymetrix, Santa Clara, CA)杂交,获得12533个基因的表达谱。基因微阵列数据可以在网址http://www.chestsurg.org.中获取。
4.2 实验结果分析
经过数据预处理后,将数据分为训练集和测试集,数据集I(多发性骨肿瘤数据集)的训练集为131个样本,包括103例正常,28例多发性骨肿瘤患者,测试集42个样本,包括34例正常,8例多发性骨肿瘤患者。数据集Ⅱ(肺癌数据集)的训练集为131例肺癌患者,109例正常基因组,22例肺癌患者,测试集50个样本,包括41例正常基因组,9例肺癌患者。使用SVM对其进行分类,选用3折交叉验证(3-fold cross-validation),将训练集随机分成3份,3次训练中每次选用2份做训练集,另外1份做测试集,并使用参数优化算法对SVM参数σ和C进行优化,参数优化算法有很多,其中最简单是网格搜索法(Grid Search),奉国和[22]介绍了使用网格搜索法在寻找支持向量机局部最优参数σ和C时,具有节约时间开销等优点。使用粒子群优化算法,传统灰狼优化算法和改进的灰狼优化算法也可以搜索最佳系数σ和C,在训练支持向量机的过程中,计算3次分类准确率的平均值作为适应度。经过200次迭代,得到以下结果见表2。
由上表可知,通过网格搜索和其他3种群智能优化算法都可以对支持向量机的参数进行优化,但是灰狼算法随机概率搜索算法,而网格搜索法是一种指定范围的穷举搜索法,所以在准确率方面3种群智能优化算法是优于网格搜索法的。群智能算法的时间复杂度高于网格搜索,但是相较与粒子群算法和传统灰狼算法,改进后的灰狼优化在时间复杂度方面有了稳定改善,且在第二组数据中,准确率也有了提升。与其他文献对比见表3。
由表3可知,通过对灰狼优化算法的收敛因子和边界进行优化,本次实验的准确率高于游伟[23]提出的SVM-RFE-SFS和高振斌[24]提出的LS-SVM。所以结合准确率和时间复杂度来看,本次实验所提出的算法对基因微阵列数据更好的分类能力。
5 结束语
本文提出了一种基于改进灰狼优化的支持向量机,使用该方法对PCA降维后的多基因微阵列数据进行分类,并使用独立测试方法获得分类准确率。通过与使用网格搜索优化,粒子群优化,传统GWO优化的SVM及其他文献提出的算法进行性能对比,可以得出该算法准确率(95.24%和94.00%)高于 其它算法,而且相较于粒子群优化算法和灰狼优化 算法,本文提出的灰狼优化算法在时间复杂度方面 有了明显改善,对临床医学应用有极为重要的参考 意义。
此次研究对灰狼优化算法的改进还存在一些不足,可以结合各个狼群的适应度,对狼的位置更新公式进行加权,或许可以再次提高算法的效率,今后可以对此方向进行深入研究。
参考文献
[1] 陈海红. 多核SVM文本分类研究[J]. 软件, 2015, 36(5): 7-10.
[2] 孙鹏, 冯翔. 一种基于集成学习的健壮性半监督 SVM [J]. 软件, 2018, 39(11): 182-186.
[3] 陈东. 癌症基因微阵列分类方法的研究[D]. 长沙: 湖南大学, 2012.
[4] 苏志同, 周文龙. 基于SVM 的心律失常的研究和分析[J]. 软件, 2015, 36(9): 98-100.
[5] 傅德胜, 经正俊. 基于PCA-LDA 和KNN-SMO 的数据碎片分类识别算法[J]. 软件, 2015, 36(7): 21-25.
[6] YU L, LIU H. Feature selection for high-dimensional data: a fast correlation-based filter solution[M]// feature selection for high-dimensional data. Springer Publishing Company, Incorporated, 2003: 207.
[7] LIU Y. Wavelet feature extraction for high-dimensional microarray data[J]. Neurocomputing, 2009, 72(4-6): 985-990.
[8] 吴辰文, 王伟. 一种结合随机森林和邻域粗糙集的特征选择方法[J]. 小型微型计算机系统, 2017, 38(06): 1358-1362.
[9] Chiaretti, S. Gene expression profile of adult T-cell acute lymphocytic leukemia identifies distinct subsets of patients with different response to therapy and survival[J]. Blood, 2004, 103(7): 2771-2778.
[10] SUN Z, Yang. Gene expression profiling on lung cancer outcome prediction: Present clinical value and future premise[J]. Cancer Epidemiology Biomarkers & Prevention, 15(11): 2063-2068.
[11] van 't Veer Laura J, Dai Hongyue, van de Vijver Marc J, et al. Gene expression profiling predicts clinical outcome of breast cancer[J]. Nature, 2002, 415(6871).
[12] Mirjalili, Seyedali, Mirjalili, et al. Grey Wolf Optimizer[J]. Advances in Engineering Software, 69: 46-61.
[13] 张悦, 孙惠香, 魏政磊. 具有自适应调整策略的混沌灰狼优化算法[J]. 计算机科学, 2017, 44(S2): 119-122+159.
[14] SONG X, TANG L, ZHAO S, et al. Grey Wolf Optimizer for parameter estimation in surface waves[J]. Soil Dynamics and Earthquake Engineering, 2015, 75: 147-157.
[15] 蔡立軍, 蒋林波, 易叶青. 基于蚁群优化算法的基因选择[J]. 计算机应用研究, 2008(09): 2754-2757.
[16] 叶明全, 高凌云, 万春圆. 基于人工蜂群和SVM的基因表达数据分类[J]. 山东大学学报(工学版), 2018, 48(03): 10-16.
[17] 陶国娇, 李智. 带认知因子的交叉鸽群算法[J]. 四川大学学报(自然科学版), 2018, 55(02): 295-300.
[18] 赵乃刚. 惯性权重动态调整的混沌粒子群算法[J]. 软件, 2016, 37(3): 01-03.
[19] 曹盟盟, 姚文斌. 基于改进粒子群算法的虚拟机放置算法[J]. 软件, 2015, 36(12): 89-92
[20] 靳艳虹. 基于PSO的基因表达数据聚类研究[D]长沙: 中南大学, 2013.
[21] 林星, 冯斌, 孙俊. 基于边界变异的量子粒子群优化算法[J]. 计算机工程, 2008(12): 187-188+191.
[22] 奉国和. SVM分类核函数及参数选择比较[J]. 计算机工程与应用, 2011, 47(03): 123-124+128.
[23] 游伟, 李树涛, 谭明奎. 基于SVM-RFE-SFS的基因选择方法[J]. 中国生物医学工程学报, 2010, 29(01): 93-99.
[24] 高振斌. 基于最小二乘支持向量机微阵列基因特征分类[J]. 计算机应用与软件, 2019, 36(08): 288-292.
