基于多目标优化模型的库存优化分析

郑玛丽

（蚌埠学院 理学院，安徽 蚌埠 233030）

1 多目标优化模型构建

1.1 问题性描述分析

查阅文献可知，目前已有的研究大多单一的成本优化模型，虽然降低了问题难度，但也带来了不少问题。比如：（ⅰ）目前很多企业在库存管理中并没有形成一致的协同管理思想，库存管理体系不够集中，未关注内部供应链库存的不稳定要素。如：顾客订货后，为了缓解时间差，很多企业也对各种物料开展了安全库存管理。然而很多企业给定的安全库存管理量相对不够清楚，对物控员在作业过程内无任何根本性的指导价值。（ⅱ）由于对安全库存量无清晰的规定，以及在实操过程中没有进行管控，造成库存周转天数较多，仓库管理混乱，累积了较多的资金流；而且在开发库存绩效管理评价指标时，很多企业根本就不去考量供应链整个周期的属性，符合一个节点库存管理要求，便会增加另一节点库存管理的问题，无法兼顾所有，从而使得库存管理工作难以开展下去。

1.2 模型假设

（ⅰ）各公司皆有符合企业需求的最低安全库存量。

（ⅱ）各公司都存在缺货时刻，但相较于库存，其缺货量相对较少。

（ⅲ）(Q,r)作为企业库存控制的一种管理策略，其适用于各公司库存实况检测。其中：Q表示固定订货量；r表示固定订货点。

（ⅳ）对公司而言，提前需求D为独立随机变量，符合正态分布N(μDi,δDi2)特征，其中μDi为第i（i=1，2，3)个节点公司提前需求D的均值，δDi为其标准差。

（ⅴ）订货提前期L是一个不确定量，其符合正态分布N(μLi,δLi2)，其中μi表示第i个节点公司的订货提前期均值，δLi为其标准差。

1.3 模型中的目标函数

对企业来说言，库存管理的最终目标是确保用户满意，最大限度降低库存成本，增强公司竞争能力[3-8]。为此，本文以上述三方面为主要目标函数采取多目标优化计算。

考虑到酒店行业自身的高资金投入、劳动密集型、高敏感度、高竞争度、高文化性（邹益民，周亚庆，2004）的特点以及无形性文化对企业员工的深刻影响，笔者将酒店企业文化定义为：酒店企业文化是在酒店的经营管理过程中产生的并被企业员工普遍接受的企业价值观、目标愿景、行为方式等因素的总和，它反映酒店在社会关系和经济关系中的意识形态，对企业的可持续发展具有重要作用。

1.3.1 供应链各环节库存成本

供应链各环节库存成本其主要包含订购成本(ordering cost，OC)、持有成本(holding cost，HC)以及订货成本(purchase cost，PC)

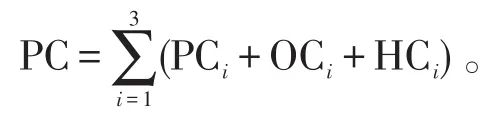
市场需求以及订货提前预期都具有一定随机性，且其分别完全符合正态分布和，进而得出各节点公司平均库存：

其中：ki代表公司最低的安全库存系数；Qi为客户预测需求量。因此企业最小化供应链库存成本函数f1可用下式表示[9-10]：

其中：Ti代表订货成本；Ui为在库的库存成本；为具有模糊属性的变化量。

1.3.2 安全库存水平

安全库存（又称保险库存）是指为了防止由于不确定因素（如突发性大量订货或供应商延期交货）影响订货需求而准备的缓冲库存，安全库存用于满足提前期需求，其属于库存管理的重要部分，是用于应对订货点出现的短期变动以及实际需求而主动设置的。企业只有保证适当安全库存，才能减少缺货现象，但如此一来则无形中增加了库存产品占有成本[11-12]。所以，对库存而言，其安全水平无法准确预测，但可用下式子表示：

其中Si表示企业库存短缺水平。因此要想保证库存安全水平f2最高则需要满足以下函数：

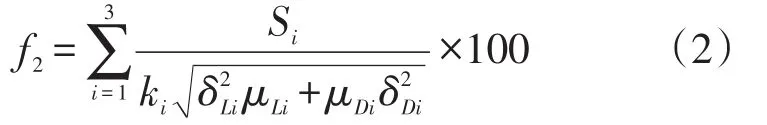
1.3.3 顾客效用水平

顾客效用水平主要表示用户需求满意情况。用户满意程度越高，其服务水平就越好，缺货情况也就越少，库存成本就会减少，库存安全水平上升，但会导致库存产品占有成本升高，反之亦然[13-14]。其对应式子为

要保证用户满意度f3最高，则需要满足以下函数关系：

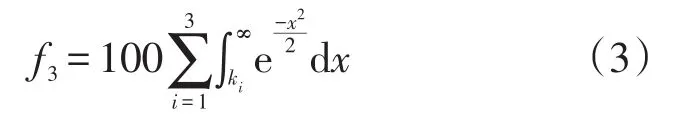
1.4 获取最佳调和解

对企业来说，如何有效调和库存成本、安全管理水平以及顾客满意程度显得至关重要。本文正是在此背景之下通过多目标优化模式来获取库存管理的最优化[15-17]。因此可以设（最大值）与（最小值），（其中j=1,2,3）。故此，对以上函数的计算分析最终得到总的目标函数vj：

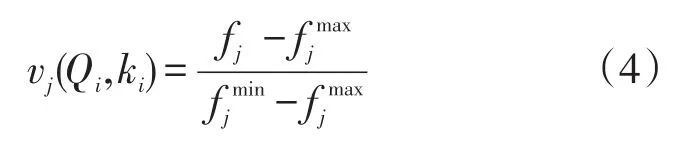
其中：fj表示公司不同的优化目标。由决策者给出各个目标的权重因子，可行解xi=(Qi,ki)的多目标函数转化为单目标函数：

则只求单目标函数（5）的最优解Qi和ki，即为供应链库存多目标优化问题（1）～（3）的最佳调和解。

另外，由于决策者的目标偏好是模糊的，则需要采用模糊语言对上述三个目标进行评价，其中模糊数和模糊语言之间的对应情况如表1[18-19]。

表1 语言变量与模糊数的对应值

采用三角模糊数Mi=(li,mi,μi),li,mi，μi∈R,i=1,2,3，且模糊数Mi处于x处的隶属度函数为：

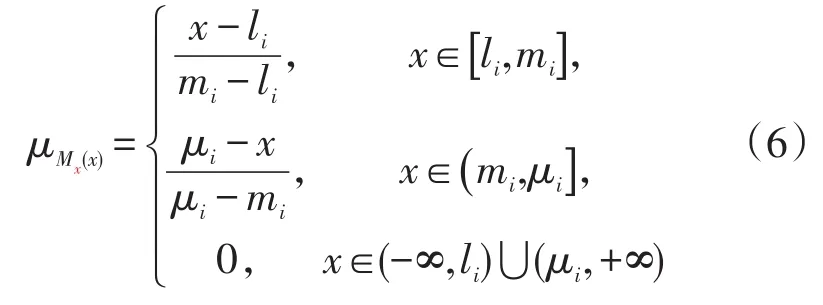
设各企业分别有Mi名专家或决策者。企业决策者便依据自身情况和相应领域专业知识，在敲定的产品价格基础上对以上目标进行模糊评价，得出评价值Mij(lij,mij,μij)(i=1,2,3,j=1,…,p)，从而构成评价矩阵M：

2 算例

为了验证本文构建的多目标库存优化模型的优化有效性，需要将多目标模型与三个单目标模型进行比较分析并进行优化求解。本小节以具体例子进行详细阐述：设顾客的预期需求是2 000件即D=2 000，相应成本等多种参数见表2。

表2 各公司的成本参数值及其它参数值

设各企业均有2名专家或决策者，其中该供应链包含6名决策人员，各自业务代表就产品价格进行谈判，最终敲定在合理范畴，随后经决策人员确定最终交易价码。然后企业决策者便依据自身情况和相应领域专业知识，在敲定的产品价格基础上对以上目标进行模糊评价，得表3与表4。

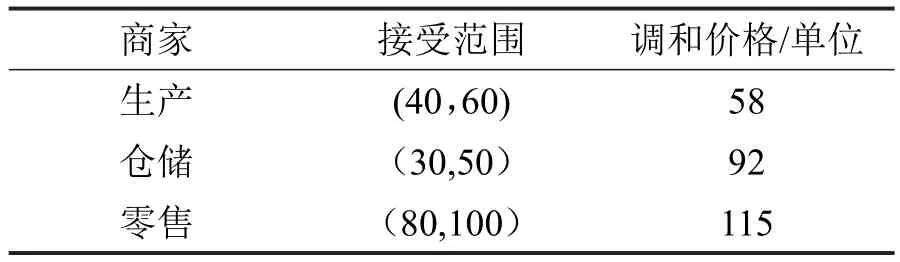
表3 产品价格调和价格与接受范围

表4 决策者对3个目标函数的模糊评价和最后权重

再得到目标产品价格以及权重之后，再根据（4）与（5）两个公式求出各个企业对应的Qi、ki值，得表5。之后把相应结果提供给各企业决策人员，不满意则修改或停止，直到满意为止。从表3与表4不难看出，不同供应链上的企业决策人员都能依据自身情况给出合理价格区间以及目标偏好值。然后再把表5的数据带入指定目标函数之中，从而保证各企业决策者能够进行全面的横向与纵向对比。上述过程决策者可多次商讨，直到得出最有方案，最终实现库存管理优化与双赢。

表5 计算得到的各企业的Qi和ki值

3 小结

本文从实际优化问题入手，从库存控制成本、安全库存水平以及顾客效用水平三方协调的基础上提出了三级供应链多目标优化模型。该模型能够实现在保证满意的顾客效用水平的情况下建立合适的安全库存，尽可能地降低库存成本[20]。该模型能够处理多品种以及复杂拓扑结构的情况，利用多目标演化技术构造了模型求解算法，得到了比较满意的结果，相对于现有单一库存优化模型本模型因为较优的整体性能和优化敏感性，具有一定的理论研究意义和更广的应用价值。