问渠哪得清如许,为有源头活水来———电源输出功率极值的教学设计和思考

◇ 山东 李统军

物理教学中知识的概括、方法的总结、题型的归类往往特别重要,而教学过程中应用一些特殊的结论,往往可以给解决某些问题带来极大的方便.但是这样的结论往往因为没有注重追本溯源的推演,而很难被学生熟练掌握和灵活运用,因此有必要在教学中重视“特殊结论”得出的过程,以此加深学生对知识的理解和记忆,进而做到熟练灵活运用,从而提升学生的物理学科核心素养.南宋理学家朱熹有一句诗,“问渠哪得清如许,为有源头活水来”,说的是“要问为何水会这样清澈,是因为有永不枯竭的源头为它源源不断地输送活水”.笔者通过电源输出功率极值的教学设计和思考,试图撬开源头活水的一角,让思维的清泉汩汩长流.

无论是新课教学还是复习课教学,教师应当具备知识点追本溯源的能力,以此增强学生对概念和公式的理解和记忆.

【教学片段1】利用闭合电路的能量守恒定律,引出功率的定义.

根据能量守恒定律,非静电力做的功应该等于内外电路中电能转化为其他形式的能的总和,即W＝Q外＋Q内,所以EIt＝UIt＋I2rt.如果等式两边同除以时间t,可得EI＝UI＋I2r.

由此引发学生对等式两边的讨论,教师进而引入电路中三个功率的定义,并进行相应分析.

1)电源的总功率P总＝EI.物理意义：描述电源内部非静电力做功的快慢,也可以理解为提供电路电能的快慢.P总、I成正比关系,P总-I图象为过原点的倾斜直线,图象斜率k＝E.适用条件：适用于一切电路.

2)电源的输出功率P出＝UI.物理意义：描述电源外部静电力做功的快慢,也可以理解为外电路消耗电能的快慢.P出、I并非简单的正比关系,因为I的变化会引起U的变化,当无法直接得出P出的时候,可以通过作差法间接得出P出＝EI－I2r.由此引发学生的思考,得出这其实是一个开口向下的二次函数,对称轴在I轴正方向.适用条件：适用于一切电路.

3)电源的热功率P内＝I2r.物理意义：描述电源内部静电力做功的快慢,也可以理解为内电路消耗电能的快慢.P内、I显然也是二次函数的关系,开口向上,对称轴为P轴,因为I不能取负值,所以为二次函数的半支.适用条件：适用于一切电路.

点评

电路的能量守恒公式是得出功率表达式的源头,再与P-I关系图象相结合,更利于功率公式的理解和记忆.

例1某同学将一直流电源的总功率P总、输出功率P出和电源内部的发热功率Pr随电流I变化的图象画在了同一坐标上,如图1中的a、b、c所示,由图象可知( ).

A.反映Pr变化的图象是c

B.电源电动势为8V

C.电源内阻为2Ω

D.当电流为0.5 A时,外电路的电阻为6Ω

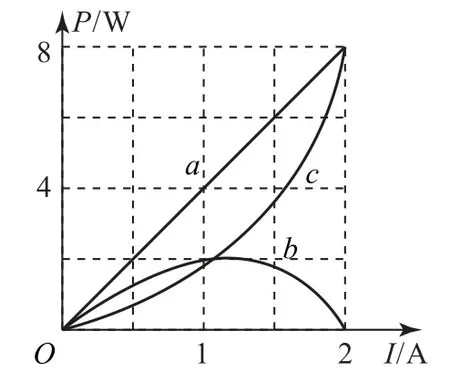
图1

解析

a为P总-I关 系图象,根据P总＝EI可得E＝4V.b为P出-I关系图象,根据P出＝EI－I2r可得r＝2Ω;c为Pr-I关系图象,再根据闭合电路欧姆定律可得当I＝0.5A时,R＝6Ω,正确答案：A、C、D.

点评

根据图象和表达式的数形关系,再结合待定系数法可以求出电源的电动势和内阻.再结合闭合电路欧姆定律和已知条件,即可求出外电阻的大小.

【教学片断2】如何求解电源的输出功率的最大值?

电源输出功率何时最大呢? 要解决这个问题必须从输出功率的表达式入手.不同的表达式会产生不同的解题方法.

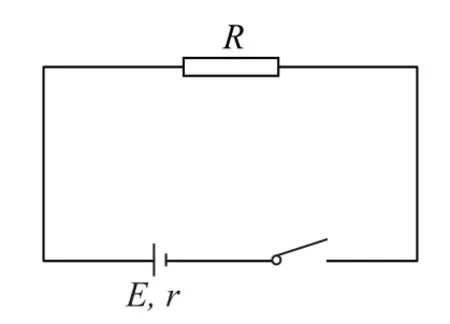
图2

方法1因为P出＝EII2r,所以我们可以应用二次函数最值法求解P出的最大值.根据P出-I的图象利用数形结合思想不难得出：当I＝的时候,输出功率取最大值,为.结合图2所示电路,根据闭合电路欧姆定律,当R＝r时,电源输出功率最大.

方法2直接利用P出＝I2R,并结合闭合电路欧姆定律将电流代入,推导过程如下：不难看出,分母部分是我们熟悉的基本不等式的形式,当且仅当R＝r时,输出功率最大,最大值依然等于

如此可以总结出电源输出功率最大的规律：当R＝r时,输出功率最大,且R可以理解为外电阻的等效总电阻.

点评

所谓殊途同归,虽然采用的数学方法不同,但是得出的结论却是相同的.

【教学片断3】规律的得出无疑给解题带来了很大的方便,当外电路结构复杂,解题难度增大时,是否可以继续沿用得出的结论呢?

例2如图3 所示,电源电动势E＝2 V,内阻r＝1Ω,电阻R0＝2Ω,可变电阻的阻值范围为0～10Ω.求可变电阻为多大时,R上消耗的功率最大,最大值为多少.

分析仔细分析会发现,本题与我们得出的结论似乎没有直接的联系,因为题中要求的是滑动变阻器R的最大功率.如果按照正常的思路分析依然可以通过两种数学方法得出R功率的最大值.但这样的解题方式太费力,而直接应用得出的结论,将会事半而功倍.

我们可以将电源和电阻R0看成一个整体,作为一个等效的新电源,如此可变电阻R的最大功率就转化为等效电源的最大输出功率了,而等效电源的内阻r′＝R0＋r.因此当滑动变阻器R＝R0＋r时,输出功率最大,且最大值为

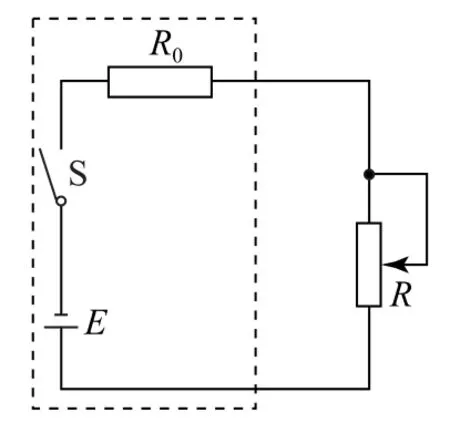
图3

点评

采用等效电源的方法,方便而快捷,不需要复杂的推导验算过程,有助于培养学生的发散思维,加深其对规律的拓展和应用.可见规律本身也可以成为求解问题的源头,即可以直接利用结论求解.

【教学片断4】规律的直接运用一般都是有条件的,当无法满足规律的条件时,我们又该怎么处理呢?

例3如图4 所示,E为电源电动势,r为电源内阻,R1为定值电 阻 (R1＞r),R2为可变电阻,以下说法正确的是( ).

A.当R2＝R1＋r时,R2获得最大功率

B.当R1＝R2＋r时,R1获得最大功率

C.当R2＝0时,R1获得最大功率

D.当R2＝0时,电源的输出功率最大

分析当R2＝0 时,电路的电流I最大,根据P＝I2R1不难得出此时R1的功率最大.因为R2是变量,等效电源法是建立在内阻是定值的基础上推导得出的,所以选项 A 正确,选项B 错误,选项C 正确.根据已知条件R1＞r,我们发现无法满足R1＋R2＝r的条件,即无法根据前面描述的电源输出功率最大的结论对选项D 进行分析,那么此时该如何处理呢? 我们也可以通过作出P出和外电阻R的关系曲线进行求解.

图4

作出如图5 所示的P出-R图象,不难看出当外电阻R无法达到与内阻r相等的时候,外电阻和内电阻阻值越近,电源的输出功率越大,这同样适用于等效电源的处理.由此可以得出选项D 也是正确的.

图5

点评

任何规律的得出都是有一定条件的,如果不能满足条件,规律也无法应用,这时就需要更加细致地审题,选择合适的方法解决问题,避免思维定势的影响.

综上所述,通过4个教学片断的设置,以问题链的方式,层层深入,不断加深学生对电路功率公式的理解和运用;以不同题型的变化,深入浅出,让电源输出最大功率的结论和等效电源法深入人心;再以题目条件的细微变化,提醒学生在运用规律时需要分析是否符合结论的条件,如果不满足则需另辟蹊径,迂回作战.对于学生来说通过这样的教学设计无论是对基础知识的理解,还是问题解决的能力、思维的发散、细节的处理等物理学科的基本学科素养都得到了显著的提升.物理课堂就是需要探寻源头活水,激发学生的潜能,增强学生的自主探究能力和理解运用能力.