考虑重力的带电微粒在磁场中的运动

◇ 广东 李 晨

不计重力的带电粒子垂直射入匀强磁场,粒子将在入射平面内做匀速圆周运动,这是高中物理电磁学部分的典型问题,但一个重力不能忽略的带电微粒在磁场中将做怎样的运动呢?

1 带电微粒以水平方向的初速度射入一个竖直方向的匀强磁场

带电微粒在竖直方向的运动与磁场平行,不受磁场的影响.于是,在洛伦兹力和重力的共同作用下,微粒实际的运动为水平方向的匀速圆周运动和竖直方向的自由落体运动的叠加,其轨迹应是处在某个圆柱体侧面上的一条等直径、变螺距的螺旋线,如图1-甲所示.由于竖直方向的运动特点,如果将圆柱体的侧面展开,运动轨迹应能拼接成一条完整的抛物线,如图1-乙所示.

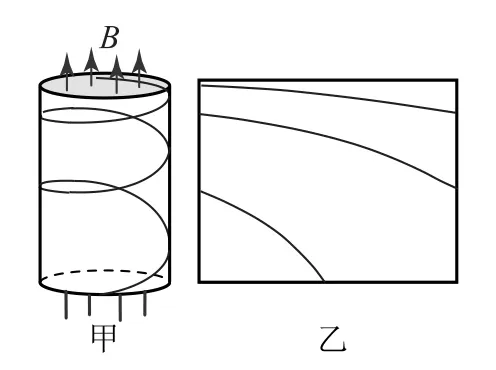
图1

2 匀强磁场方向水平,带电微粒沿垂直于磁场的方向水平入射

例如,一个质量为m、重力不能忽略且带电荷量为＋q的带电微粒,以水平初速度v0向左射入垂直纸面向里的匀强磁场中.为了看清其运动轨迹,不妨设带电微粒具有一对等大且反向的分运动速度,在图2中用v和v′表示.由于它们是同时存在,因而不会对微粒的实际运动有任何影响.假如则与向右的速度v′对应的洛伦兹力Fv′＝qv′B＝mg,且方向向上,可将重力抵消.微粒由于具有向左的初速度v＋v0,而受到的洛伦兹力为Fv＋v0＝q(v＋v0)B.于是可把微粒运动看成下列两个分运动的合成：1)水平向右的匀速直线运动,速度为v0),周期的逆时针方向的匀速圆周运动.所以微粒的合运动仍是在同一竖直面内的周期性曲线运动.但其轨迹曲线不再封闭,而是一条向右伸展的螺旋形曲线,如图3-甲所示.

其实在这种情况下,不论初速度v0方向如何,带电微粒的运动轨迹都是一类名叫“旋轮线”的数学曲线.它们和一个正在水平地面上匀速滚动的车轮边缘上的某些点相对地面的运动轨迹相似.例如,图3-乙所示的等幅旋轮线(摆线)是带电微粒在v0＝0时的运动轨迹,它和车轮的边缘某点的运动轨迹相似.而图3-丙所示的短幅旋轮线是带电微粒初速度v0向右(且)时的运动轨迹,它和车轮轮毂上某点的运动轨迹相似.

图3

3 磁场方向水平,带电微粒以水平初速度平行磁场入射

如图4所示,三维坐标系的z轴负方向表示匀强磁场B的方向,带正电的微粒从y轴上的P点沿z轴负方向以速度v0入射.因为初速度v0沿B方向,故微粒在此方向上的运动不受磁场影响.由于垂直于B方向无初速度,微粒应和图3-乙中描述的运动相似,故此时微粒的运动可看成三个分运动的叠加：1)在xOy平面内做半径周期的逆时针匀速圆周运动;2)沿x轴正方向以速度做匀速直线运动;3)沿z轴负方向以速度v0做匀速直线运动.微粒的运动轨迹是一条比较复杂的三维曲线,但不难发现其在xOy平面的投影就是图3-乙所示的曲线.

综上所述,笔者讨论了考虑重力的带电微粒在匀强磁场中运动的三类不同情况.结果说明,即使微粒不再做匀速圆周运动,我们仍可以利用运动的叠加原理去定量计算其在某时刻的速度或位置情况,甚至还可将其推广到质点在任意其他恒力(如电场力)与洛伦兹力共同作用下的运动学问题的计算.

图4