采用分数阶临界阻尼控制律的动力吸振器研究

陈炎冬，陈 宁，徐 俊

（1.无锡太湖学院 机电工程学院，无锡 214064；2.南京林业大学 机械电子工程学院，南京 210037）

0 引言

在振动的结构上附加吸振器是控制结构振动的有效措施之一[1]。动力吸振，在受控对象上附加一个质量-刚度-阻尼子系统，用它产生的控制力来部分或完全抵消受控对象受到的激振力。这时，子系统“吸收”了主系统的振动，故称子系统为动力吸振器。经典的吸振器技术是通过耦合辅助系统使主系统的振动发生转移，也就是使主系统的振动能量在主系统和从系统之间重新分配达到控制主系统的振动，缺陷是有效的吸振频带是在一个很狭小的带宽范围，并且不可调节。为了解决这些问题，出现了一些自适应调谐减振器[2～4]，以及变质量、变刚度甚至是零刚度、负刚度的吸振器[5～8]，正在成为研究热点。

上世纪三十年代，Gemant，A.[9]观察到粘弹性材料动刚度的数学模型，如果引入分数导数可以得到更理想更准确的表达。从此分数阶在工程中的应用研究越来越多，其中带分数阶阻尼的动力吸振器研究开始出现[10～12]，陈宁[10]等研究了具有分数阶阻尼的吸振器，通过数值仿真结果表明，分数阶阻尼吸振器的减振作用正介于无阻尼吸振器和粘性阻尼吸振器之间，则可以调和无阻尼和粘性阻尼吸振器的矛盾，选择最佳的被动式吸振器。但阻尼大小采用试凑或采用优化的方法选取。关于动力吸振器的控制研究和参数优化的方法也在不断涌现[13～17]，但目前还很少用临界阻尼来设计控制律，而本文将从临界阻尼定义[18]出发，将传统整数阶临界阻尼拓展到分数阶临界阻尼，在研究其特性的基础上针对经典的主动动力吸振器进行分数阶临界阻尼的控制律设计并对其进行试验验证，得出合理选取控制参数的方法和步骤。

1 分数阶临界阻尼理论

首先基于单自由度分数阶自由振动系统如式(1)所示，讨论分数阶临界阻尼理论。

x(t)表示位移，0Dαx（t）表示位移的分数阶导数，m、c、k分别为质量、阻尼和刚度系数。这里0Dαx（t）采用Caputo定义，如式(2)所示。

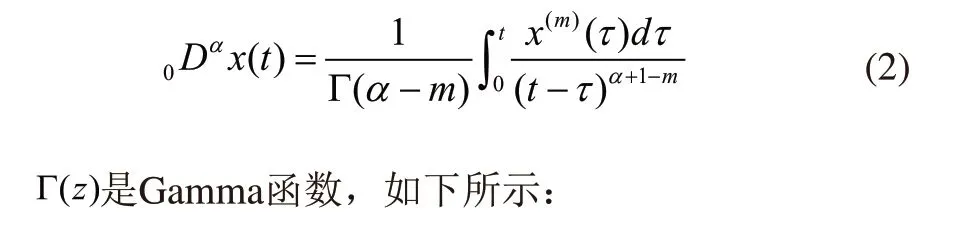
根据等式两边实部虚部分别为0，当特征根虚部rsinθ不为0时，系统会产生振荡，为了避免振荡和发散，特征根实部必须是负的即rcosθ＜0，且虚部为rsinθ=0。假设θ=（2k1+1）π，k1为整数，则上式可简化为：

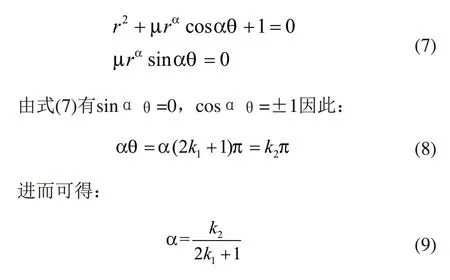
从式(9)可以看出α只有分母为奇数，分子为与分母互为质数的整数时才存在。如3/5、7/9、8/11、14/11等等。从式(7)可以看出当cosαθ=1时，可以算出特征根实部是正的，表示有外界的能量输入系统，振荡会越来越强，系统是发散的，相反，当cosαθ=-1时，可以算出特征根实部是负的，系统是稳定的。

综合上述推导可得到存在临界阻尼的条件：当k1，k2为整数，且互为质数，α∈（0，2），cosαθ=-1时有：

其中r∈R+，式(10)当du/dt=0时，可得在极值位置时的r值，r=（α/(2-α））1/2，当系统参数确定后，归一化后的系统只能通过分数阶阶次来改变其临界阻尼，将式(4)的变换条件代入式(10)得原系统的阻尼与特征值幅值之间的关系式：

当α=1时，极值位置时的r=1，代入上式可得临界阻尼为cc=，与传统二阶系统临界阻尼一致。

下面探讨：1）c与r之间的关系；2）分数阶阶次对系统响应的影响；3）系统阻尼与系统振荡之间关系4）当有干扰后，分数阶临界阻尼与整数阶阻尼的作用影响。固定仿真参数：初始位移x0=0.01m，初始速度v0=0m/s，m=10kg，k=1000N/m。

根据式(11)可以绘制出c与r之间的关系图，如图1所示。

图1 不同α时系统阻尼随特征值幅值变化曲线

图2 不同α时系统位移响应曲线

图1为不同分数阶阶次α时系统阻尼随特征值幅值变化的关系曲线，从图1中看出当系统存在分数阶阻尼项后，临界阻尼大小可以通过改变分数阶阶次来设计系统需要的值，但是必须满足前面理论推导的临界阻尼存在条件。

图2为在初始位移x0=0.01，初始速度v0=0，α分别等于8/11，1，14/11时系统位移响应曲线，可以看出当分数阶阶次小于等于1时系统没有振荡，大于1会有一定的振荡，说明当分数阶阶次α∈（1，2）时从物理角度解释该材料特性已经不是α∈（0，1）粘弹性材料特性，而是介于粘性和刚性之间的混合材料，所以在刚性部分作用下会有一定的超调量。

图3为在初始位移（0.001m）激励下的系统位移响应，其中图3(a)和图3(b)分别表示α=8/11和α=14/11时，不同系统阻尼时系统位移的响应曲线。讨论了临界阻尼的作用，当α=8/11系统阻尼大于等于临界阻尼时，系统响应指数收敛，且看出c＞cc时收敛速度小于临界阻尼时的收敛速度，c＜cc时虽然响应快，但是有明显的振荡。当α=14/11系统阻尼大于等于临界阻尼时表现出来的响应和α=8/11时有一定的区别，虽然取了临界阻尼但是存在小幅度的超调量，也印证了图2中α=14/11的曲线现象，α=8/11，c＜cc时一样有明显的振荡。

图4是在阶跃力激励作用下，不同α时系统位移响应，同样可以看出α∈（0，1]时，取临界阻尼时系统没有振荡，而α∈（1，2）系统有振荡。

图3 在初始位移（0.001m）激励下的系统位移响应

图4 不同α时系统位移阶跃响应

综合上述可以得出一个结论，对于单自由度振动系统，当采用阻尼项的分数阶阶次α∈（0，1]，阻尼系数采用临界阻尼cc，可使振动系统有效的避免振荡；当α∈（1，2），该项表现出既有阻尼又有刚性的作用，此时系统在理论临界阻尼时也有振荡，因此无法避免振荡，但可以通过设计小于临界阻尼的阻尼，使系统振动尽量小。

2 动力吸振器的分数阶临界阻尼控制律设计

2.1 动力吸振器建模和解耦

图5 动力吸振器模型

根据牛顿第二定律可得动力吸振器的动力学模型：

m1、m2为主系统、吸振器的质量，k1、k2分别为主系统、吸振器的刚度，c1、c2分别为主系统、吸振器的阻尼，u为控制输入，f(t)为主系统上受到的干扰。

根据式(12)改写为如下矩阵形式：

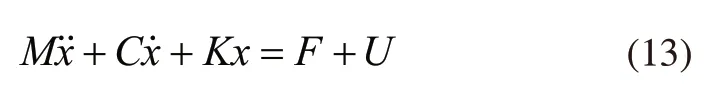
其中质量矩阵、刚度矩阵、阻矩阵尼、控制矩阵及干扰矩阵如下表示：

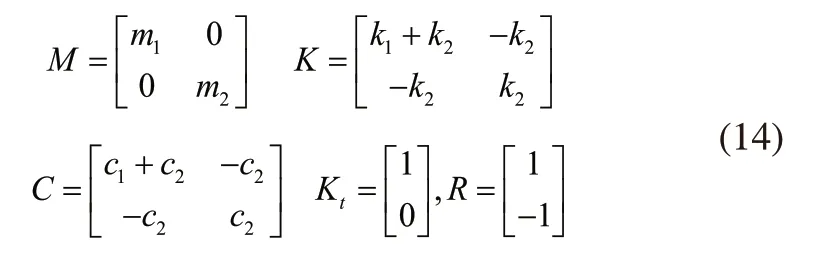
假设Φ为该系统的特征向量矩阵，令X=Φη，并代入式(14)得：

如果C为对角阵，则系统可以完全解耦，现实中大部分系统的阻尼是无法完全解耦的，本文的动力吸振器的结构参数下也无法得到对角阵，因此这里根据主对角线占优[19]的方法来设计系统阻尼，即主对角线元素绝对值之和大于次对角线元素绝对值之和，从而忽略阻尼矩阵次对角线上的，则阻尼矩阵转化为对角阵C=diag（Cp1，Cp2），从而系统实现近似解耦，下节设计分数阶临界阻尼控制律以此近似模型来推导。

当然这里必须讨论下忽略次对角线线元素带来的误差大小。为了分析近似解耦模型和原模型之间的误差大小，假设系统没有外界激励和控制输入，则式(15)可以表示如下形式。

根据式(12)和式(16)、式(17)分别绘制在相同初始条件下，近似系统和实际系统响应曲线的对比图如图6所示，主系统的位移和速度响应图如图6(a)、图6(b)所示。从图中可以看出近似系统和实际系统的位移和速度存在误差，对实际系统和近似系统在5秒里的主系统位移和速度的比较分析如表1所示，从表中可以两个系统的均值和均方差存在一定的误差，但是还可以看出两个系统位移、速度之差绝对值的均方差的数量级比原系统的均方差小两个数量级左右，说明利用近似模型来进行设计分数阶临界阻尼是有一定精度保证的。

2.2 分数阶临界阻尼控制律设计

根据2.1的推导，可将动力吸振器系统进行近似解耦，看成两个独立的单自由度振动系统，因此根据第2部分的单自由度分数阶临界阻尼的理论分析，对其进行分数阶临界阻尼控制律设计。动力吸振器的分数阶临界阻尼项，具体形式如下所示。

图6 近似系统和实际系统响应曲线的对比图

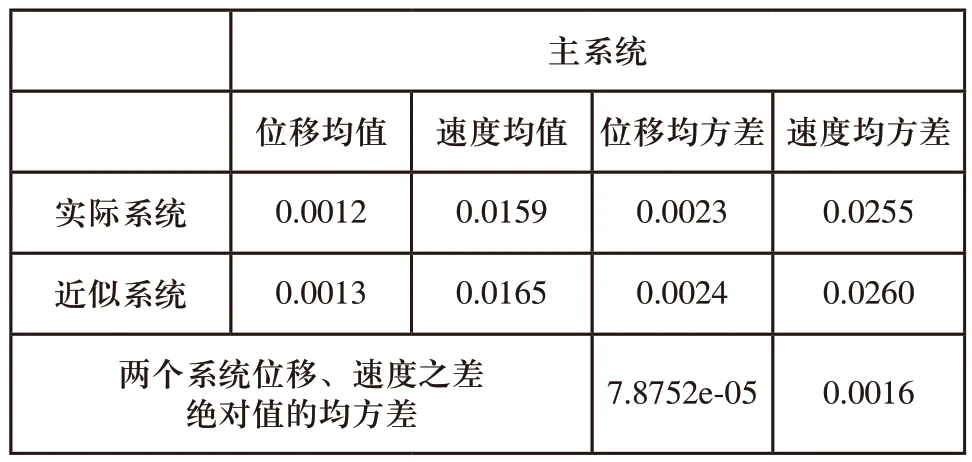
表1 主系统位移与速度均值和均方差

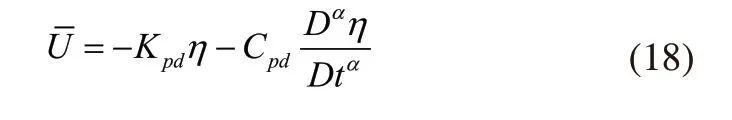
其中Cpd为控制输入分数阶导数项系数，代入式(15)有：

根据第2部分，单自由度振动系统的分数阶临界阻尼推导，同理可推得动力吸振器分数阶临界阻尼的关系式如下:

对式(21)求导，导数为0时，得到：

将其代入式(21)，可得到最优临界阻尼系数cc，因此控制律中阻尼项系数Cpd=cc=diag（Cpdi），i=1，2，而且控制律中还有一个比例系数Kpd，这里考虑主系统为不可调参的固定系统，因此其中的Kpd1取0，只需要调节另一个Kpd2就可以快速寻到最优参数。

最后将X=Φη代入U得分数阶临界阻尼控制律：

由于式(23)中的ΦTR不是方阵，所以这里用(ΦTR)+表示广义逆矩阵。

3 仿真试验分析

动力吸振器的结构参数：m1=50kg，m2=10kg，k1=15000N/m，k2=8000 N/m，c1=800，c2=400。首先分析Kpd=0时，即控制律中只有一项分数阶临界阻尼项进行控制，来分析分数阶阶次α和其系数Cpd对系统振动大小的影响。

图7和图8分别为当分数阶阶次分别为8/11，1，14/11的分数阶临界阻尼控制和当时的被动控制。在阶跃幅值为0.1干扰激励下主系统的位移响应和在采样周期为0.1s，功率0.001的白噪声干扰激励下主系统的位移响应。

图7 主系统的阶跃位移响应

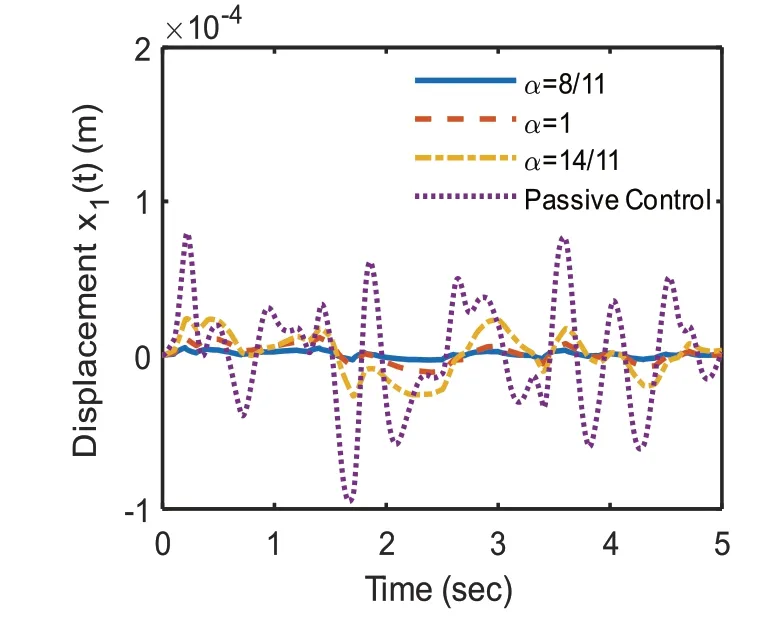
图8 不同α时主系统的白噪声位移响应

从图7中可以看出，没有补偿阻尼项的被动控制最敏感且振动幅度最大，分数阶阶次取8/11时上升时间最大，5秒后振动幅度最低。从图8中白噪声激励干扰下同样可以看出，普通的整数阶临界阻尼效果比阶次大于1和被动控制时的效果好，但是分数阶阶次8/11的性能明显比整数阶时更好，说明本文提出的设计方法，只要合理选择分数阶阶次和其对应的临界阻尼，就可以进一步提升减振效果，印证了上一部分的结论。

进一步分析在临界阻尼附近的特性，选择分数阶阶次为8/11，阻尼取0.5cc、cc和1.5cc时，比较其减振效果。图9为不同阻尼时主系统的白噪声响应，其中图9(a)、图9(b)分别为当分数阶阶次8/11时的采用不同阻尼时的主系统和吸振器位移比较图。从图中可以看出，取小于分数阶临界阻尼振动波动大，而且发现大于分数阶临界阻尼时，减振效果提升的幅度很小，说明取0～1之间满足分数阶临界阻尼条件的数，就可以有效的提升系统减振性能，而不需要进行复杂的在线优化，而且满足该条件的数有限，使动力吸振器的控制律参数设计更加简洁。

图9 不同阻尼时主系统的白噪声响应

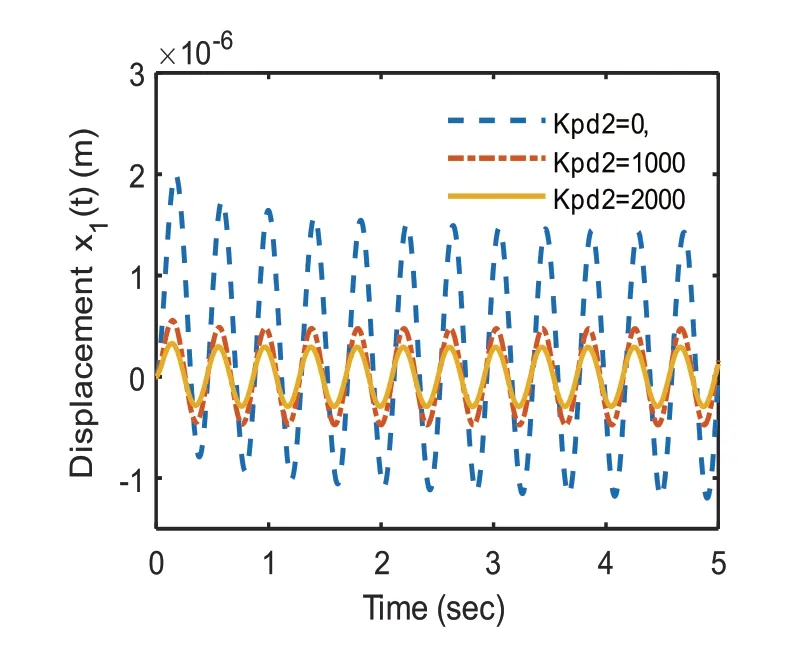
图10 当α=8/11时，不同比例系数时的简谐响应

当然本文提出的控制律还有比例控制项，即当Kpd不等于0时，从式(21)看出，通过调节其大小可以改变临界阻尼的大小，同时还从式(20)看出，会改变系统的固有频率大小，从而改变吸振器的减振效果。这里绘制了当激励为0.1sin(ωt)，ω为主系统的固有频率，α=8/11；Kpd1=0；Kpd2=0，Kpd2=1000，Kpd2=2000时的对比分析，如图10所示，可以看出当Kpd1=0；Kpd2=0时系统振动幅度最大，而通过调节吸振器的比例控制系数，避开主系统固有频率，从而在合理选择α的基础上进一步有效的降低了主系统的振动幅度。

4 结语

本文给出了单自由度振动系统分数阶临界阻尼存在条件，并在此基础上进行了动力吸振器的减振控制研究，得出以下结论。

1）通过对单自由度振动系统在初始干扰下的振动分析，发现分数阶阶次变化体现出一些特殊物理意义，当阻尼项分数阶阶次α∈（0，1）时，阻尼材料具有粘弹性特性通过调节α使粘性和弹性特性比重进行调节，α=1时就是传统的粘弹性材料特性，而当α∈（1，2）时，该项表现出材料既有粘性又有刚性的特性，当然也可以调节α使粘性和刚性特性比重进行调节。

2）采用主对角线占优原则对动力吸振器模型进行解耦和误差分析，近似模型引起的误差较小，下一结论验证了方法的有效性。

3）利用近似模型设计了分数阶临界阻尼控制律，并在实际模型进行试验是有效的，而且该控制律参数选取方便。（参数选取步骤：取小于1同时满足分数阶临界阻尼条件时的分数阶阶次α，然后通过调节控制律中的吸振器对应的比例系数Kpd2，最后根据式(21)、式(22)计算得到分数阶临界阻尼系数cc）。