基于遗传算法的航天零件仓库货位优化研究

李 阳，唐 磊，胡 俊

（东华大学 机械工程学院，上海 201620）

0 引言

现代物流将存储、运输、装箱搬运等信息结合一体，满足客户多样性的要求。所以，物流在企业的组成中占有很重要的位置。自动化立体仓库（AS/RS）管理却是物流供应链最关键的一环，而在立体仓库管理中，实现货位优化提高仓库运转效率一直是一个难题，有效的货位分配能提高货物出入库效率和库位使用率，这是节省企业成本的有效途径。因此，对自动化立体仓库货位分配优化是一个亟待研究的课题，具有重要的现实研究价值。

当前，国内外学者基于立体仓库货位优化的问题，已经开展大量研究，积累了许多研究方法和实际应用案例[1～6]。常见的货位分配策略主要有：定位存储策略、随机存储策略、就近存储策略、分类存储策略、共享存储策略等。Rao等以库存分布密度为出发点，提出了一种基于类别的存储策略，引入优化分区的数学模型，计算出非常接近实际的拾取行程。Paul Berglund提出了一种在解决给定存储策略下，建立了单跨中通道优化布局的解析模型，选择在交叉通道最佳位置优化选择器移动距离问题的方法。Moghaddam M等在研究动态存储分配问题时，基于产品的ABC分类和相互关联性，提出了一种基于产品相似性的启发式技术，极大的提高了平均拣货时间。李珍萍在研究储位优化问题时，将产品按ABC分类法，提高了拣货效率和库存使用率。Kao等对某饮料公司的商品进行ABC分类管理，建立大型零售商和小型零售店的经济订货量库存控制模型，模型仿真证明提高了仓储管理的效率。Yueting.C等讨论了自动化仓库中存储区域的划分和存储分配原则，提出了仓库存储区域优化的数学模型，将出口频率高的货物放在靠近货架出口。

虽然货位分配优化在国内外的研究已经非常广泛，但是从以上的综述可以看出，针对不同的实际货位优化问题，分配策略的选用是有很大的差异的，而且对双升式货架的研究很少。本文研究的航天零件自动化立体仓库是双升式货架，需要考虑货物周转情况下的翻库情况。此外，存储零件种类规模大，但是批次小，而库存量有限制，一旦库位分配不合理，就会造成出库次序混乱，完成订单的效率低下。针对这种问题，文中提出基于模拟退火遗传算法的存储策略进行货位分配优化研究，为零件合理分配货位，提高仓库库位的使用率和出库效率。

1 问题描述

与其他立体仓库不同，航天零件的仓储系统具有以下特点：

1）存储零件的特殊性。一般用于航天上的零件都比较精密，大多以小型为主，而且种类繁多。文中研究的航天零件大都是多品种、小批量的。选取该企业三个月的订单数据分析，如图1所示，横坐标表示货物种类，纵坐标表示货物数量。仓库中总共需要储存的零件可达1900多种，种类冗杂，而且每类零件的数量有较大差异，这大大提高了仓库的存储难度。

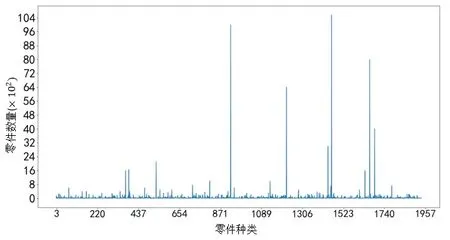
图1 立体仓库存储的零件种类及数量

2）零件出入库的特殊性。由于入库作业具有不确定性，平时主要以存储零件为主，每3个月周转一次，完成零件出库作业。作为物流中转部，需要对现场生产提供需求，满足现场的生产节拍。所以，对零件出库效率有很高的要求。

3）货架布局的特殊性。要完全按不同种类存储这些航天零件，所需的仓库面积是非常大的。但是现在由于受到场地的限制，只有有限的空间存储这些零件。所以，立体仓库货架的布局会对零件存储数量会产生重要的影响。如图2所示，两排货架为一组，采用双深式货架，可以增加货物存放量，同时减少占地面积。

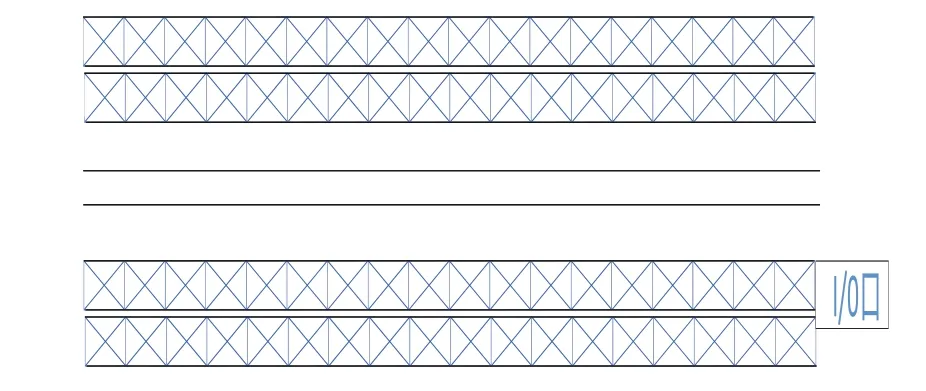
图2 立体仓库货架示意图

2 货位优化模型

2.1 模型假设

根据研究的航天零件立体仓库货位问题的描述，为方便模型的建立，简化研究对象，文中对研究目标提出如下假设条件：

1）双深式货架，令靠近I/O口一侧作为内侧，远离I/O口一侧作为外侧。

2）堆垛机货叉两级伸缩，左右两边都能执行出入库操作，即堆垛机能够接触到立体库的每个库位。

3）货物都是放在中转箱中，所有货位能够放下货箱，且每个库位货物种类只有一种。

4）堆垛机的水平和垂直方向上的运动都是服从匀加速或匀减速运动，且堆垛机能够同时进行水平和竖直方向上的运动。

5）每个库位货格的规格，即每个货位的尺寸都保持一致。

6）每一类货物出库的频率能够进行恰当的预测，得到合理的结果。

7）由于堆垛机货叉出入库的时间占总操作时间的比例很小，所以可以忽略不计。

8）立体仓库内的I/O口在同一侧。

2.2 模型中各变量的定义

文中研究的航天零件仓库模型的参数大致如下：

1）双深式货架，共X排Y层Z列，km,n,o（m=1，2，3，…，X；n=1，2，3，…，Y；o=1，2，3，…，Z）示该货物处于第m排n层o列。设定立体仓库出入库的起始点位于k2，1，0紧靠出入库平台的库位为第一层和第一列，且最左边的货架为第一排。

2）Mxyz表示x排y层z列库位中货物的重量；

3）Qxyz表示库位（x，y，z）中货物的数量；

4）H表示货格高度，L表示货格长度；

5）Vz表示堆垛机在水平方向上的平均速度；

6）vy表示堆垛机在竖直方向上的平均速度；

7）fxyz表示（x,y,z）货位储存货物的平均出库频次；

8）txyz表示对应生产周期内（x,y,z）货位零件出库数量；

9）S表示一个周期内所有出库零件的总数量。

2.3 目标函数及约束条件

根据航天零件存储库位的特殊性及堆垛机运动相关参数，考虑立体仓库中货物出库效率和货架稳定性之间的关联，建立自动化立体仓库的多目标货物优化模型。

1）基于零件出库效率的分析

由于文中研究的立体仓库入库作业具有不确定性，所以主要研究货物出库效率。而出库效率主要以堆垛机周期运行时间为依据，将所有零件出库所需的最小时间作为出库效率研究目标，建立第一目标函数如下：

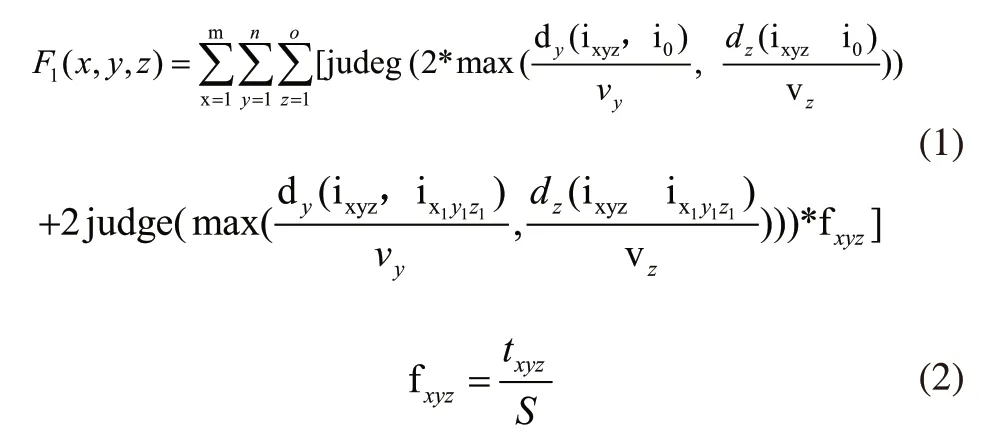
式中，dy（ixyz，ix1y1z1）表示出库位到周转位竖直方向位移，dz（ixyz，ix1y1z1）表示出库位到周转位水平方向位移，第一个judeg表示判断库位是否有货，若judeg=0，则库位无货，不需要出库。第二个judge表示判断库位是否需要翻库，若judge=1，则需要翻库。

2）基于货架稳定性的分析

货架稳定性与货架整体重心高低有关，现在普遍的研究方法是将较重的货物尽可能的摆放在底层，较轻的货物放在高层，做到“下重上轻”，这样会减小货架的整体重心，提高货架的稳定性，建立第二目标函数如下：

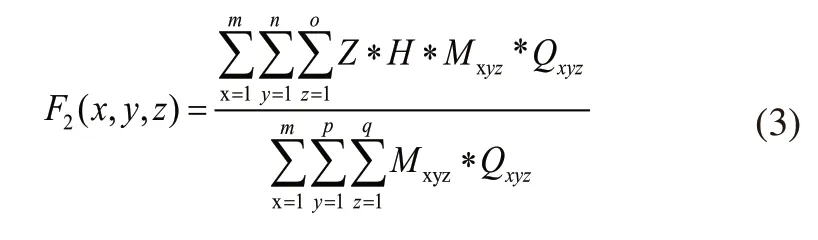
式(3)中，将每个货格中货物总重与所在层数、货格高度乘积之和，再除以每个货格货物总重之和。

由于双深式货架的特殊性，每一组货架都是由两排货架组成的，而且货架在横向方向上的长度要远远大于纵向方向上的长度，所以为保证货架抗倾覆的稳定性，需要额外考虑每一组的两排货架x=2p-1和x=2p，p∈N且p∈[1，m/2]总重量基本保持一致。据此，建立第三目标函数如下：

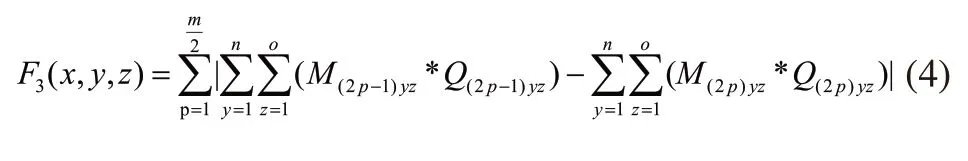
式(4)中，将同一组的外排货架每个货位总重跟里层货架总重之差作为平衡水平稳定性指标

3）约束条件：结合文中研究的仓库模型，总共有m排货架，每排货架又有n层o列，x、y、z分别表示立体仓库中货架的排、层、列。因此，货位优化模型问题的空间约束条件如下：1≤x≤m；1≤y≤n；1≤z≤o；x、y、z均为正整数。

2.4 多目标函数归一化

在研究多目标函数时，要综合考虑每个目标函数各自之间的关联及影响关系，从而达到各个目标函数在给定的条件下，尽可能接近最优解的目的，从而达到多目标函数的最优化。文中采用模拟退火遗传算法，根据现场实际合理分配权重，将多目标函数问题转换为单一目标函数。

多目标函数中，F1（x，y，z）指最小出库时间，单位是秒（s）；F2（x，y，z）指货架的竖直重心尽可能低，F3（x，y，z）指货位的水平重心坐标尽量靠近中心，这两个目标函数无量纲。由于三个目标函数的单位不一致，在进行多目标函数归一化处理时，只需要对F1（x，y，z）归一化，取最大和最小的两个确定数值及参数∂，处理后的归一化目标函数为：

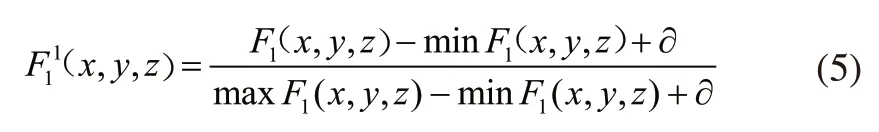
将三个目标函数赋予不同的权重 αi（i=1，2，3），将其转换成单目标函数如下：

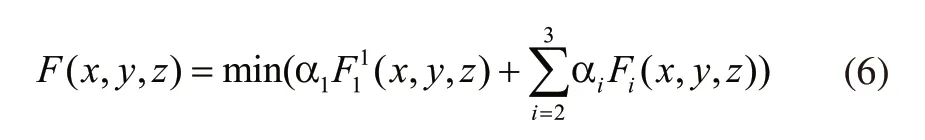
3 基于模拟退火遗传算法的存储模型

遗传算法作为一种智能优化算法，应用范围广，具有自然界生物选择和遗传的特点，在算法求解过程中，能够很好的运用自身交叉、变异来快速寻求最优解，并且具有在全局范围内搜寻优秀解的能力。然而，遗传算法极易陷入早熟、收敛的缺陷，局部搜索能力不是很理想的问题，所以需要对它进行改进，跳出局部收敛，找到优秀解。而模拟退火算法是在模拟固体物质退火时，从开始的高温慢慢下降到低温过程中，会以一定概率跳变，能够很好的在一定范围的解空间中随机寻找所需的最优解。将模拟退火算法的跳变性与遗传算法进行融合，能很好的弥补遗传算法早熟缺陷[7,8]。

3.1 染色体编码

选用合理的染色体编码方式对优化问题有很大的帮助，不仅能简化问题难度，而且还能提高遗传算法的求解速度。一般的遗传算法编码技术主要有：二进制编码、实数编码，但是由于二进制编码方式在解决货位优化问题时，其随机性会使得遗传算法局部搜索能力较差，在逼近最优解时，变异后的子代跟父代的差异性很大，不连续，导致最优解极其不稳定。因此，文中主要采用实数编码的方式来进行染色体编码，将货物种类、每类货物库存实例及货物坐标杂糅成一条染色体[16]，表达形式如下：

1）染色体中基因所在的位置代表着库位中货物的三维坐标Lijk（i—排，j—层，k—列），展开后的一维坐标如下：

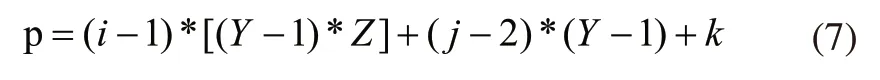
2）每一个库位中货物的实例采用实数m（m∈W）+小数n（n=.000，.001……，Nw）的形式，实数m代表库位中货物种类，小数部分代表该类型货物在库中的实例编号。

3）结合基因位置和货物实例，p位置基因表达情况如下：

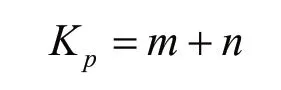
假设现有两排货架，每排货架都是4层3列，库中有5中不同类型的货物。由于立体仓库第1层与堆垛机平行，不存放货物，故从第2层开始存放货物，染色体基因编号从L1，2，1开始。K1=1.001指染色体中第一个基因：货位L1，2，1存储的是货物类型1的第一个。图1的货位分配方式形成的染色体k=k1k2…k9，这些组成了遗传算法的一个可行解。

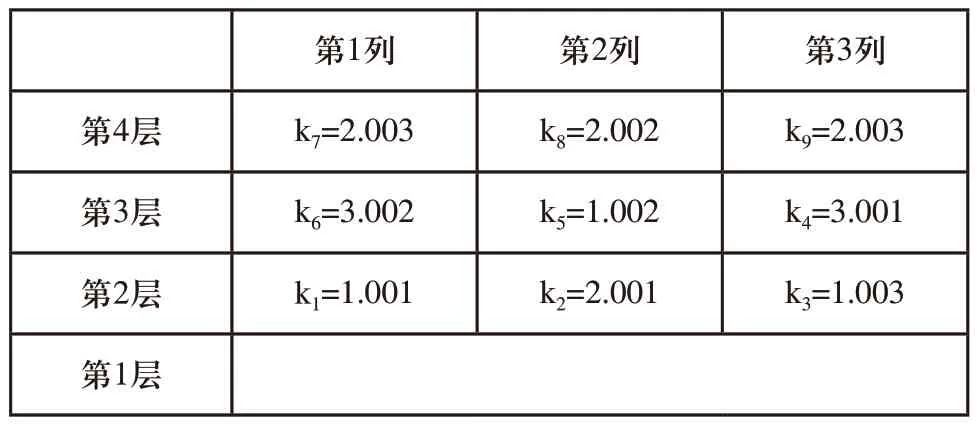
表1 货位与基因编码示意

3.2 适应度函数

遗传算法中，适应度函数可以衡量每代种群中各个体接近最优解的优秀程度，可以通过适应度值近似确定每代种群最优个体。文中将出库时间和出库稳定性的三个目标函数转换成研究的适应度函数。经过变化后的适应度函数如下所示：

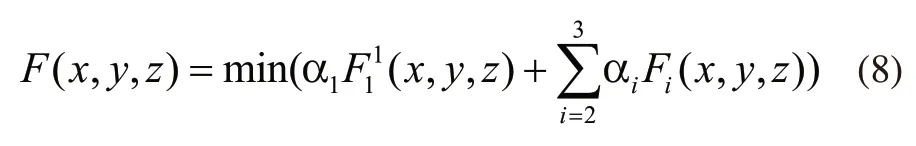
3.3 选择算子

文中采用k=2的锦标赛选择算子。锦标赛选择是一种比较流行的选择策略，主要思想是：在整个种群中取若干个个体，让他们互相竞争，最终得到最优个体。选取锦标赛算子，可以将竞争后的优秀个体进行选择交叉、变异等操作，使其直接进入下一代种群。

3.4 交叉算子

交叉操作可以为遗传算法每代种群带来新个体的补充，具有不可忽视的地位。适当的交叉方法，可以加快遗传算法的运算效率，提高目标函数的优化结果。张春涛[9]在研究TSP问题时，发现均匀两点交叉遗传算子相较于传统的两点交叉算子有较好的优越性。所以，文中采用均匀两点交叉算子。

3.5 变异算子

变异算子可以提高种群的多样性，帮助遗传算法脱离陷入局部收敛的现象。文中采用多次变换变异算子，并引入自适应性函数调整变异概率。杨志龙[10]在研究仓储货位优化时，在基于Srinival，M等人提出的一种自适应遗传算法（AGA）基础上，改进的自适应函数能有效的得到全局最优点，帮助遗传算法跳出局部收敛，为每代种群提供多样性个体。

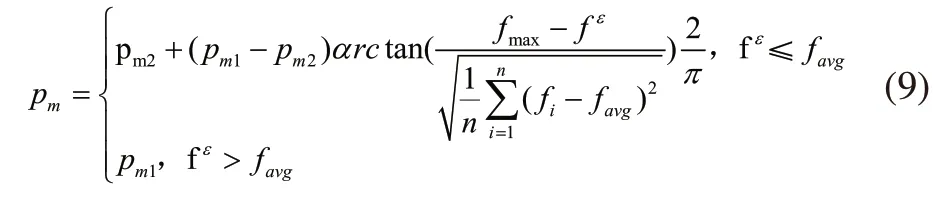
其中，Pm1、Pm2：变异率大、小界值；fmax、favg：当前种群最大、平均适应度值，fε：变异个体适应度值。

3.6 模拟退火算法（SA）操作

引入模拟退火算法是为了利用它的跳变性，在很大空间搜寻近似最优解，从而帮助遗传算法跳出局部收敛，得到最优个体。文中拟定的模拟退火操作：先设定一个停止阈值温度Tmin，在遗传算法一系列操作后产生新的种群中，选择一部分优秀个体进行SA操作，根据Metropolis的接受准则进行判断是否接受新解，其接受准则如下：

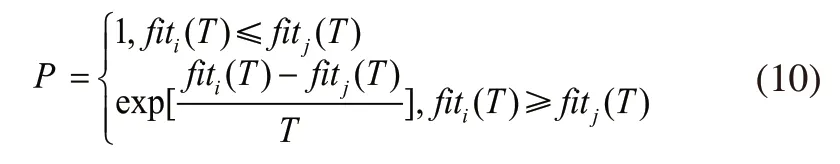
其中，fiti（T）表示经过遗传算法操作产生新个体的值，fitj（T）表示个体经过SA操作后的值。在每一次迭代中，如果当前温度T＞Tmin，则进行降温操作，tk+1=β*tk，β∈[0.5，0.09]为降温系数；否则，结束循环。

模拟退火优化遗传算法（SAGA）基本流程如图3所示。

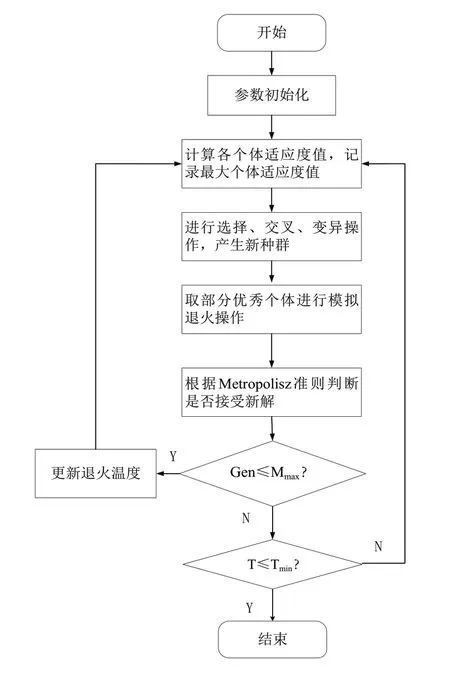
图3 模拟退火优化流程

4 仿真结果分析

4.1 基本参数设定

1）文中研究的航天零件立体仓库相关参数配置及历史订单数据均来自某航天零件制造研究所立体仓库的实际情况。相关参数如表2所示。

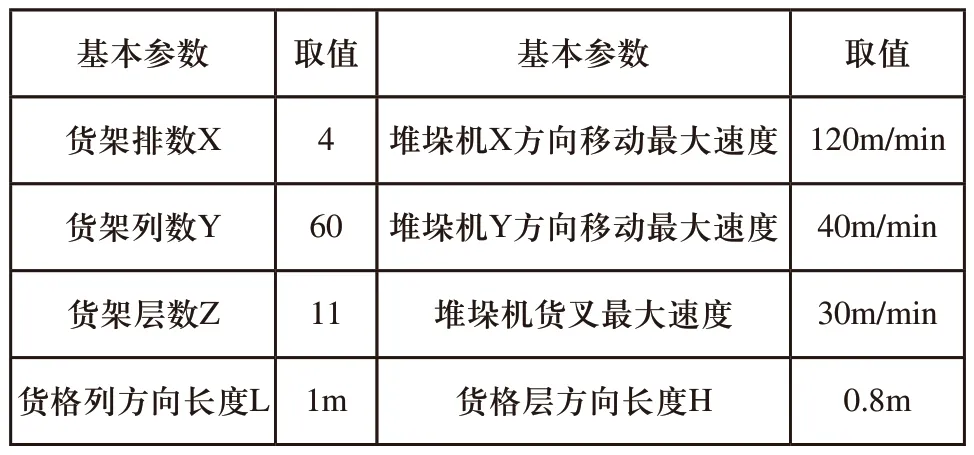
表2 立体仓库基本参数

2）SA-GA算法控制参数及终止条件

本文中拟定种群初始大小为50，迭代次数为500代；交叉概率为pc=0.95，变异概率范围为[0.008，0.01]；初始温度T= 100000；阈值温度Tmin=100，降温系数β=0.95；当前温度低于Tmin时，算法运行结束。同时，根据仓库货物的实际情况，对每个目标函数进行权重赋值，分别是：W1=0.7，W2=0.15，W3=0.15，将设定的参数应用到算法中。

4.2 仿真结果

本文设计的算法由python语言编写实现，利用四种分配策略：基于改进遗传算法的存储（SA-GA）策略、就近存储策略（COL）、随机存储策略（RS）和ABC分类存储策略（ABC），对文中建立的模型进行仿真模拟，对比这四种货物分配策略的优劣性。文中，COL策略是将出库频率高的货物存储在离出口近的货位；RS分配策略是随机给每个货物分配货位；ABC策略是将货架按一定比例将货架分成三类，按照货物平均出库频率的高低将货物放在分类的货位中，货架分配比例是1：2：7。

1）从图4可以看到，传统的遗传算法容易陷入局部僵局，接近300代左右才收敛，并且解的质量差，难以获取迭代最优解。然而，将模拟退火算法融入遗传算法后，如图5所示，遗传算法快速达到收敛状态，在100代左右就开始收敛，最终解接近全局最优解，质量好，算法效率极高。

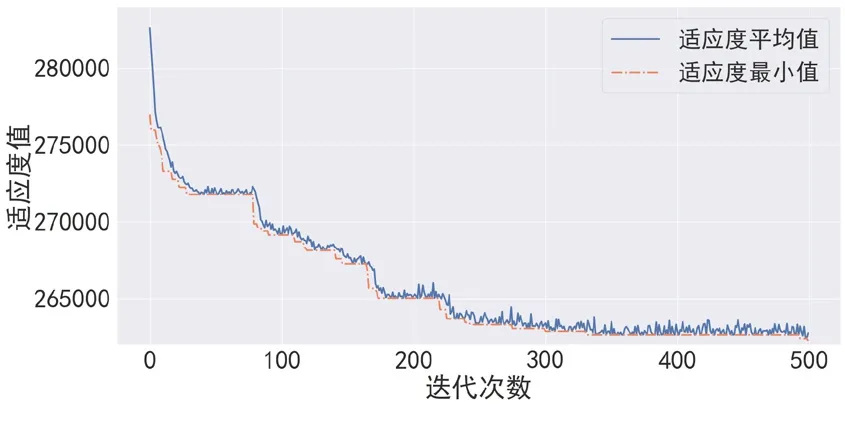
图4 传统自适应GA收敛曲线

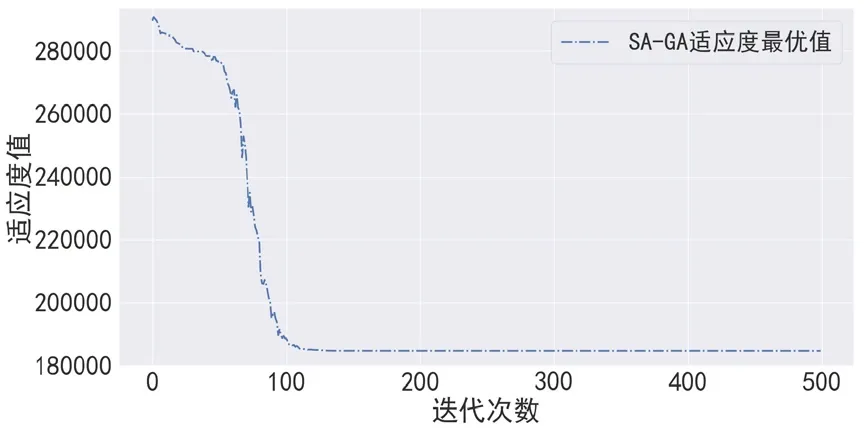
图5 SA-GA收敛曲线

2）在表3可以看到，SA-GA的结果优于其他三种存储策略，其中表示的出库时间分别降低了11.7%，9.6%，55.7%；表示的货架竖直重心分别降低了39.7%、68.2%、57.6%；表示的货架水平重心分别降低了26.3%、63.1%、58.6%。

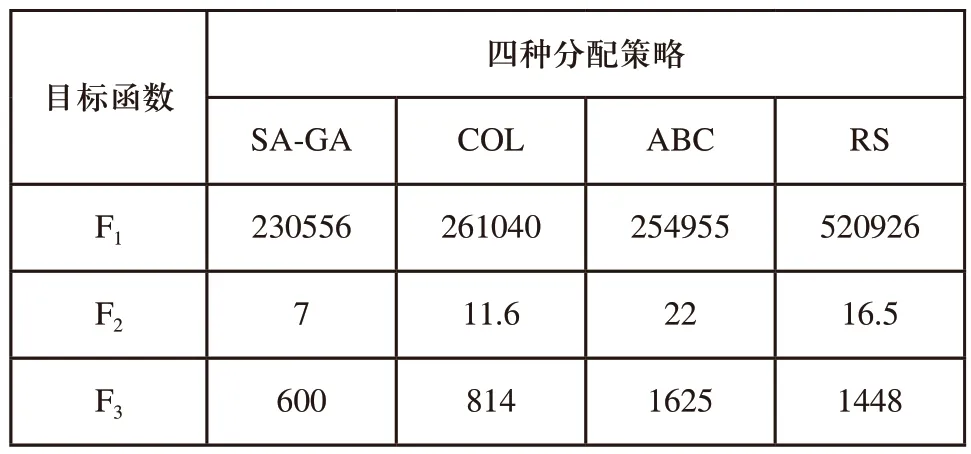
表3 四种分配策略目标函数值对比

5 结语

本文主要从提高自动化立体仓库货物出库效率和货架稳定性这两个方向出发，以航天零件自动化立体仓库为研究对象，构建了三个数学模型，利用四种存储策略进行仿真分析，比较这四种分配策略的优劣性，同时将遗传算法跟模拟退火算法很好的融合，使遗传算法跳出局部收敛。通过立体仓库历史订单数据进行仿真求解，得出基于模拟退火遗传算法的存储策略在出库效率和货架稳定性上的性能要优于其他三种货物分配策略。同时，文中研究的立体仓库货架是很特殊的双深式货架，目前研究这方面的理论还比较少，所以，在这方面的研究还有可继续深入的空间，如在建模过程中的假设条件跟实际存在一定的冲突性；建立的模型在实际的立体仓库中不易实现等等。