基于ADAMS的传动系统对主轴稳定性的影响分析

程 洋，黄鹏鹏

（江西理工大学 机电工程学院，赣州 341000）

0 引言

“万向节-传动轴-传动系统” 广泛存在于船舶传动装置、轧机主传动系统、重卡传动系统、客车传动系统和飞机轴系等[1～3]，这种柔性传动系统可以保证导致振动、冲击和能量损失问题的扭矩以浮动点的方式输出[4]。由于汽车变轴传动系统是汽车的关键部件，减振降噪和提高车辆质量是环保的必然趋势，也是政策要求。因此，研究传动系统的振动是至关重要的。减少变轴传动系统的振动和冲击，实现传动系统的节能，降噪和安全运行，是研究人员在许多重要工程应用中的重点。

时培明[5]等研究了带有间隙的多自由度主传动系统的动力学模型，结果表明改变间隙和扭矩扰动值可以减小扭转振动的幅值。Gnanakumarr[6]等人认为，高频率会导致传动系统轴件的某些结构模式发生振动响应。王三民[7]等人验证了随着支撑刚度的变化，弧齿锥齿轮系会经拟周期分岔进入混沌振动。Itoh[8]在理论上研究了传动系统中减小瞬态振动时间对控制参数的影响，并用实验加以验证。Hotaita和Kahraman[9]通过一组关于正齿轮对的实验值说明了动态因子和动态传递误差之间的线性关系。上述文章主要研究间隙，时变网格刚度，齿轮传动系统高频振动或者参数对齿轮啮合的影响。然而，很少有研究人员关注传动轴和主减速器之间的匹配性能。当传动轴工作正常的时候，某个万向节会产生速度波动，导致额外的振动和噪声[10～12]。此外，振动会通过凸缘和其他部件传递到主减速器，导致主减速器的振动增加。

本文以某微型车的传动轴和主减速器为研究对象，采用虚拟样机仿真的方法，设置不同的轴间角度，不同的中间支撑刚度，研究传动轴对主减速器噪音和振动的影响，并查明传动轴对主减速器振动影响的作用规律，为改善传动轴与后桥的参数匹配奠定了坚实的基础。

1 模型建立

1.1 传动轴模型

车辆的传动轴主要由十字轴万向节、两根传动轴管、两根滑动条、一个中间支撑、一个法兰等部分组成，主减速器主要由主被动螺旋锥齿轮、主减速壳体、连接法兰和锁紧螺母组成[13]。传动轴的模型如图1所示。

图1 传动轴组件

通过UG软件建立微型车传动轴和主减速器相关部件的三维实体模型，为简化数值模拟过程且满足仿真结果的需要，忽略对仿真结果影响微弱的小零件，只保留主要部件[14]。将三维模型导入到动力学分析软件ADAMS中。其最终简化模型如图2所示。

图2 传动轴-主减速器的简化模型

1.2 模型前处理

在进行虚拟原型模拟前，必须在组件上添加运动学约束。传动轴绕其自身的轴线旋转，齿轮箱和第一传动轴之间的运动副通过一个旋转副模拟，交叉轴万向节围绕其自身轴线旋转。因此在三个关节约束上采用了一个旋转副，如图3所示。

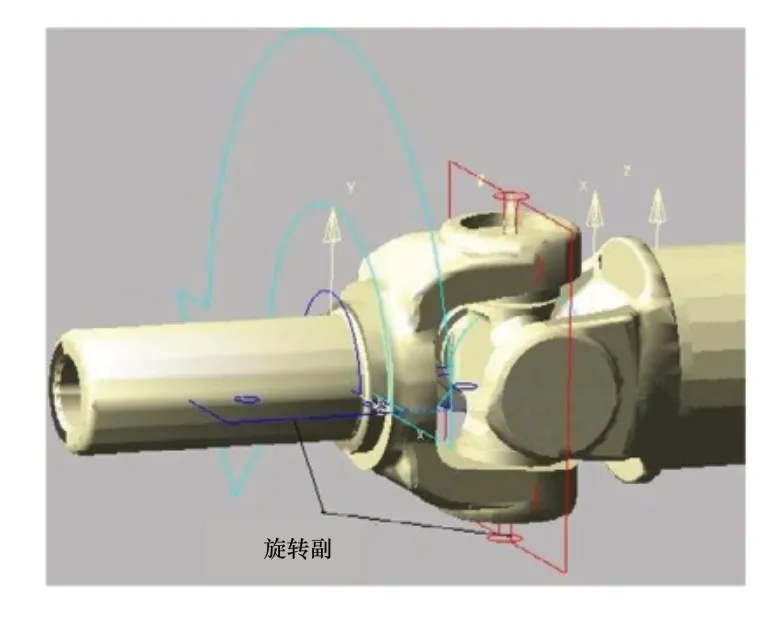
图3 万向节运动副

平移副用于滑动花键和万向节主动叉之间的运动副，在轴向运动过程中模拟滑动花键的实际运动。中间支撑由圆柱副连接到传动叉并通过固定副连接至地面，因此可以模拟中间支撑的实际运动状态，如图4所示。

图4 滑动花键运动副

车辆输出传动轴通过一个耦合法兰与主减速器的主动伞齿轮相连，从而实现发动机的动力传递。在仿真模型中，省略了联接法兰机构和主动齿轮轴端的花键联接；输出轴与主动螺旋锥齿轮直接通过旋转副连接以实现动力传递。从动螺旋锥齿轮的旋转轴线垂直于其端面，通过旋转副模拟从动齿轮的约束，如图5所示。

图5 主从动齿轮副

2 传动轴-主减速器的虚拟仿真分析

2.1 轴间夹角对角加速度的影响

某微型车传动轴的第二部分长度为875mm，既仿真模型的第二节长度为875mm。在仿真过程中，改变第二段轴的下移距离可以实现轴间角度的变化。通过设置轴间角为0°、2°、5°、8°、10°，分别对应于第二节轴向下移动距离为0mm，-30.5mm，-76mm，-121.8mm，-152mm。将第二段轴的向下移动距离定为设计变量，主减速器主从动螺旋锥齿轮的角速度作为目标函数。由于微型车的发动机转速为2500r/min，换档次数为2，通过研究主被动齿轮的动态响应，得出不同轴间角度下的主动齿轮和从动齿轮的角速度波动曲线如图6、图7所示，角加速度波动曲线如图8、图9所示。

图6 主动齿轮角速度曲线

图7 从动齿轮角速度波动曲线

图8 主动齿轮角加速度曲线

图9 从动齿轮角加速度曲线图

传动轴-主减速器的输入角速度函数为STEP（time，0，0，1.2，1500d），由图6、图7可得，当轴间角度从0°变化到5°时，主从动齿轮的角速度波动幅度逐渐减小，而当角度从5°变化到10°时，角速度波动幅度逐渐增大。角度值从0°变化到10°（0°，2°，5°，8°，10°）对应于Trail_1至Trail_5。从图中可以看出，第三次仿真得到的曲线波动值最小，既第三次模拟产生的主减速器的噪声和振动最小。通过图8、图9所示仿真曲线表明，当轴之间的夹角为5°时，主动齿轮和从动齿轮的振动最小，与图6、图7所得结论一致。

2.2 中间支撑刚度对后桥噪音和振动的影响

当轴间夹角为5°时，传动轴可以更为有效的传递角速度，并且对主减速器的噪音和振动影响较小。因此，采用控制单个变量的方法，假设轴间夹角为5°，分析主动齿轮与从动齿轮的接触仿真，并研究中间支撑刚度对主减速器噪声和振动的影响规律。由上文所得结论，中间支撑刚度值一般在100N/mm～1500N/mm之间。将中间支撑的模拟模型替换为衬套。对衬套X、Z轴方向的刚度值进行设置并模拟中间支撑与花键之间的力学关系，其仿真模型如图10所示。

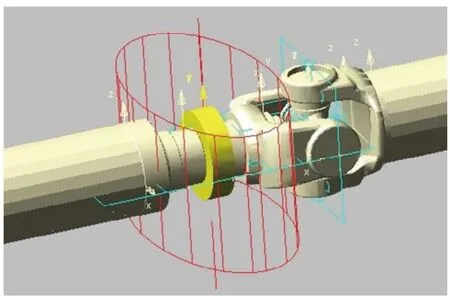
图10 传动轴中间支撑处衬套模型

套管在X 轴和Z 轴方向的可变刚度值设置为[1.0E+5，2.0E+5，...，1.5E+6]。在仿真中，创建如图11中所示的两个设计变量（DV_3_stiff_ness_x和DV_4_stiff_ss_z），其变量值分别对应X和Z轴方向上的刚度值。由于X轴和Z轴方向的刚度值同时变化，因此采用ADAMS中的变量控制矩阵保证两个设计变量同时变化。如图11所示的可变控制矩阵形式为[-7 -7，-6 -6，-5-5 ...5 5，6 6，7 7]，通过仿真获得齿轮扭矩值，仿真曲线如图12、图13所示。

图11 仿真参数设置

图13 被动齿轮转矩随中间支撑刚度波动曲线

由图12、图13曲线可得，主动轮与被动轮转矩随中间支撑刚度波动并未呈现较大波动区间，在1.0E+5N/m到6.0E+5N/m之间出现对称状态且曲率较为平稳，并未出现较大震荡趋势，6.0E+5N/m到7.0E+5N/m之间出现短暂递减，随后递增至9.0E+5N/m处达到最大峰值。在9.0E+5N/m之后随着支撑刚度的增加，轮齿转矩逐渐递减，并在14.0E+5N/m达到一个小波峰后随之减小。当中间支撑刚度值在4.0E+5N/m到5.0E+5N/m之间时，曲率值最小，齿轮的转矩波动达到最小。

3 实验分析

本文所研究车辆的已知参数为：发动机排量为1.2L，载重量为1500kg，车轮有效半径为290mm，后桥主减速器齿数比为8∶41，中间支承刚度为700N/mm，轴间角度为7°。实验装置如图14、图15所示。

图14 传感器安装位置

图15 实验仪器

测试结果如图16所示。一个光电传感器用于测量速度，两个振动传感器用于测量轴向和垂直方向的振动。测量信号由电荷放大器放大，测出的模拟信号转换为数字信号输入计算机。当角度值变为5°，中间支撑刚度变为500N/mm时，主减速器的振动如图17所示，汽车内部的噪音值如图18所示。

图16 轴间角为7°，中间支撑刚度为700N/mm时的振动曲线

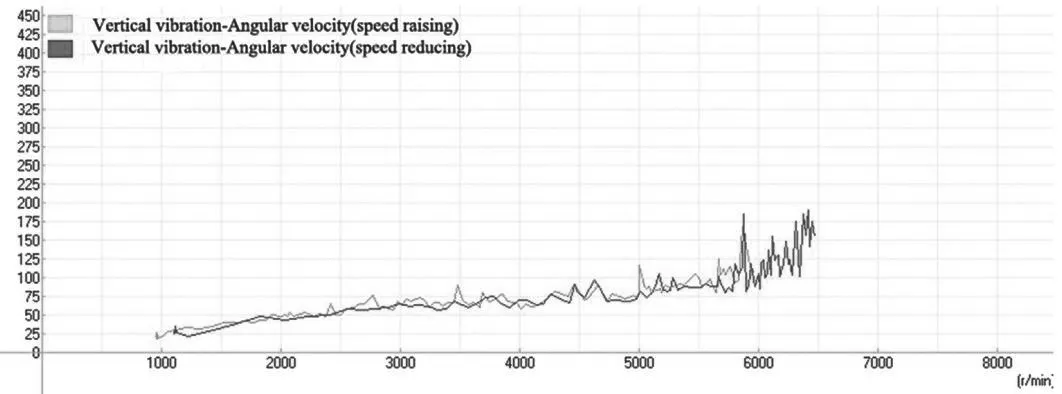
图17 轴间角为5°，中间支撑刚度为500N/mm时的振动曲线

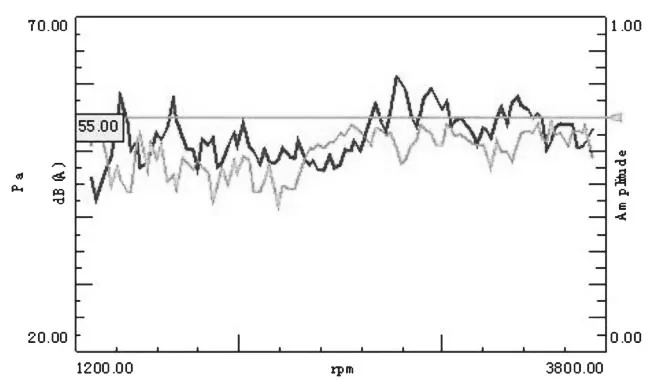
图18 汽车内部噪声图

从图16可以看出，在轴间角达到7°时，在5000r/min附近出现较大波动，且呈现出最大峰值，随着转速的增加波动趋势相对减小，在5000r/min～6000r/min之间波峰趋于相对稳定状态，在5500r/min左右震荡趋势最小，波峰值出现最小区间。由图17可得，在轴间角为5°，中间支撑刚度为500N/mm时的振动曲线基本趋于一个稳定递增趋势，在达到6000r/min时出现最大峰值，但区间波动范围极小，角速度仍然呈现缓慢递增趋势。通过对比图16发现随着轴间角、支撑刚度越小主减器振动频率越小，进而确定轴间角与中间支撑刚度对主减速器产生很大影响。最后该实验表明，当轴间角度为5°，中间支撑刚度为500N/mm时，主减速器振动和车内噪声最小，且实验结果与仿真结果高度一致、误差为5%。

4 结语

1）通过对传动轴-主减速器的虚拟仿真实验分析不同轴间角度下的主、从动齿轮角速度波动曲线，得出当轴间角度为5°时，传动轴对主减速器噪声和振动的影响最小。

2）利用动力学分析软件对主减速器主动轮与从动轮进行模型构建，进行齿轮啮合接触仿真模拟，研究中间支撑刚度对主减速器噪声和振动的影响规律，结果表明中间支撑刚度约为500N/mm时，主减速器的振动最小。

3）以计算机传感器测控实验系统对车辆传动轴进行信号采集，测量的信号由电荷放大器放大，将模拟信号转换为数字信号输入计算机。当角度值变为5°，中间支撑刚度变为500N/mm时，主减速器振动和车内噪声最小，且实验结果与仿真结果高度一致，经计算误差为5%。