基于支持向量机和深度信念网络的短期光伏发电预测方法
2020-08-13郭江震王福忠
郭江震,王福忠,张 丽
(河南理工大学 电气工程与自动化学院,焦作 454003)
0 引言
光伏大规模的接入电力系统会对其造成一定的冲击[1,2]。对光伏发电的准确预测有利于电力系统调度部门合理安排发电计划。
光伏发电预测方法中,间接预测法的预测精度取决于气象数据的准确性[3]。统计学方法在预测非线性部分时具有一定的局限性[4]。人工神经网络法(Artificial Neural Network,ANN)[5]容易陷入局部最优解。支持向量机(Support Vector Machine,SVM)[6,7]可以寻找到目标函数的全局最优解,但对核函数等参数的选取较为敏感。
组合预测法[8]一般采用不同的单项模型分别进行预测,再将各单项模型的预测结果经过权重计算得到最终结果,可以综合各单一模型的优点,提高预测的精度。文献[9]通过单项模型的预测结果对BP神经网络进行训练,获得单项模型的权重,避免了复杂的权重求解过程,但BP神经网络属于浅层神经网络,面对大量、复杂、多维的数据时,表征能力欠佳。而深度信念网络(Deep Belief Network,DBN)[10]具有强大的拟合能力,可以通过多层结构分层表征影响光伏发电的相关因素和其对应的光伏发电功率之间复杂的关系,因此,本文构建基于三种常见核函数的SVM预测模型作为组合模型中的单项模型,避免SVM预测模型受核函数影响,采用深度信念网络对三种单项模型的预测结果进行优化组合,克服浅层神经网络的缺点。
1 相似日的选取
传统的相似日选择算法大多通过主观赋权法对不同的气象因素进行权重分配,无法客观精确的反映不同因素对光伏发电的影响[11]。本文采用文献[11]的方法,并将气象特征向量改为每小时的温度、湿度、光照强度来选取相似日训练样本,具体原理参见文献[11]。
2 基于SVM-DBN的光伏发电预测算法
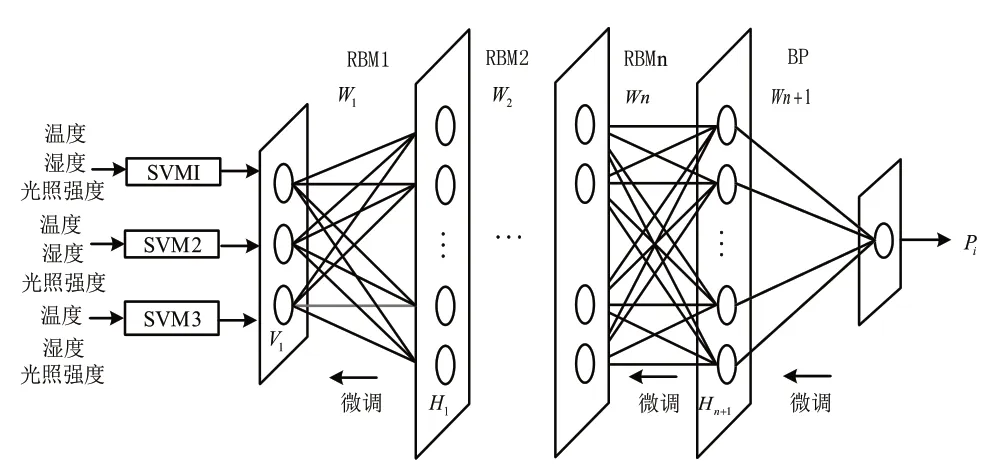
图1 基于SVM-DBN的光伏发电功率预测结构模型
建立如图1所示的光伏发电预测模型。图1中V1为RBM1的显层;H为RBM的隐含层;W为V和H的连接权重。SVM1、SVM2、SVM3为组合预测模型中三个单项模型,其输入为温度、湿度、光照强度特征向量,输出为光伏发电预测值。利用SVM1、SVM2、SVM3的输出对DBN进行训练,最后将三个单项模型待测日的预测结果输入到训练好的DBN中得到最终预测结果。
2.1 基于SVM的三种单项预测模型的构建
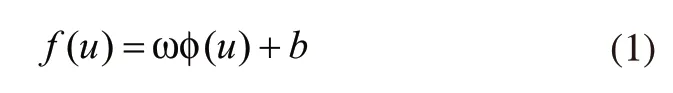
式(1)中,ω为加权向量,φ(u) 为非线性函数,b为阈值。
线性损失函数ε不敏感损失函数为:

由式(5)可以看出,在基于SVM的光伏发电预测模型中,核函数的不同会影响光伏发电预测的结果。因此本文采用三种最常用的核函数如式(6)~式(8)分别建立SVM光伏发电预测模型,并在下文中分别以SVM1、SVM2、SVM3代表即:
线性核函数(Linear):
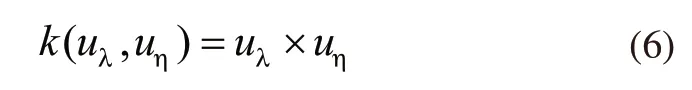
采用式(6)作为核函数的SVM预测模型在下文称之为SVM1;
多项式核函数(Polynomial):
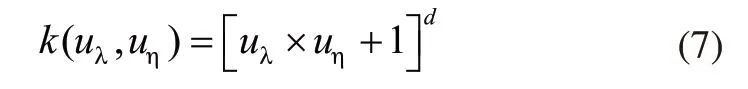
采用式(7)作为核函数的SVM预测模型在下文称之为SVM2;
高斯径向基核函数(RBF):
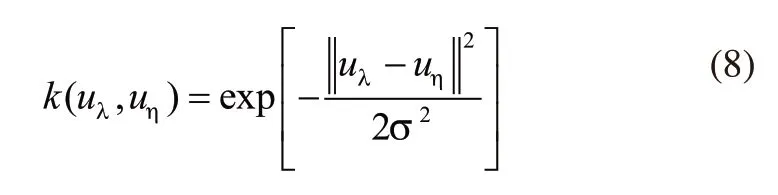
式(8)中σ为核宽度。采用式(8)作为核函数的SVM预测模型在下文称之为SVM3;
以2018-4-22的实测数据为例,对三种单一光伏预测模型的预测精度进行比较,评价方式为其在同一时刻输出与输入的误差平方Et:

式(9)中,P0t为t时刻光伏发电的实际功率,Pt为t时刻光伏发电的预测功率,结果如表1所示。
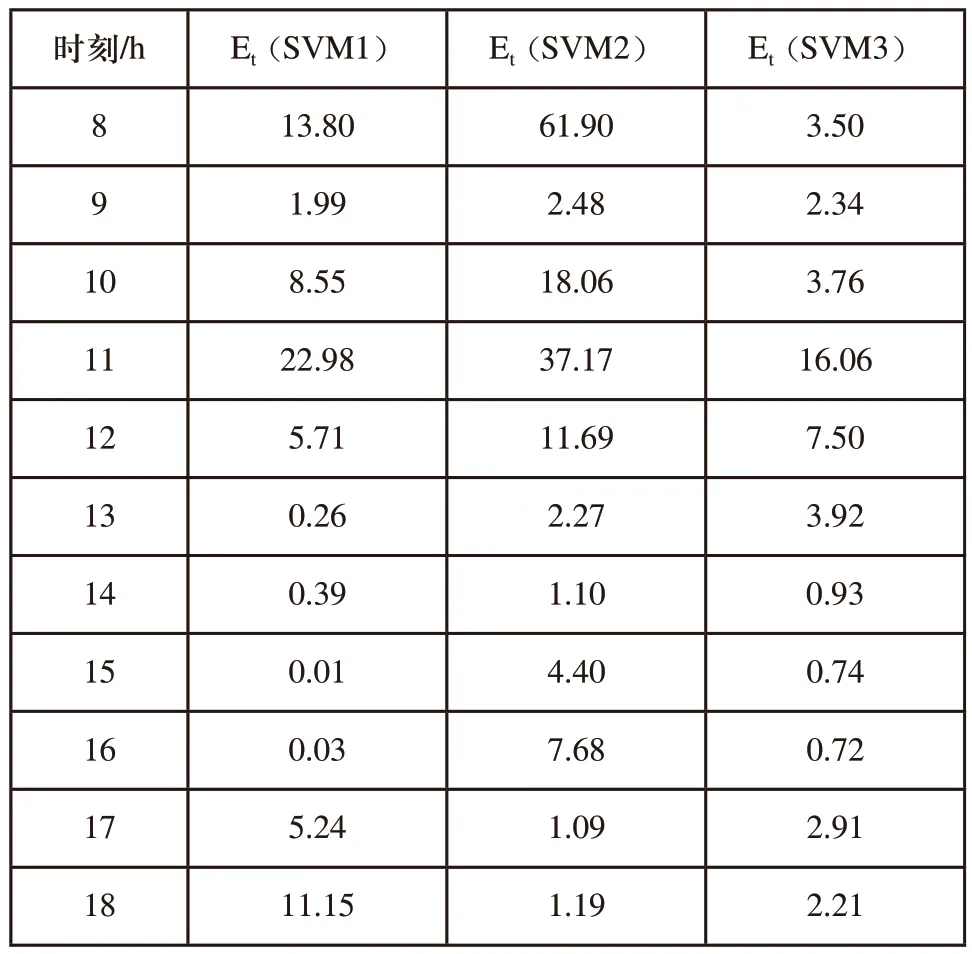
表1 三种SVM预测模型预测性能比较
由表1可以看出,在某一时刻,三种模型的预测精度各有优劣,说明三种模型之间存在着差异度[12],因此,这三种模型可以组成组合预测模型来提高预测的精度[12]。
2.2 基于SVM-DBN的光伏发电组合预测模型
三种单项预测模型构建完成后,再通过DBN对单项模型的预测结果进行组合优化,过程如下:
1)以各单项模型的预测值作为DBN的输入向量,分别由X1、X2、X3表示。
2)通过枚举法对DBN隐含层的层数及单元数进行选取[13]。再通过训练样本对DBN进行训练,从而确定各单项模型的最优权重,训练过程有两步:
第一步通过无监督的逐层训练[13]来训练DBN中的RBM。设RBM中的显层、隐含层神经元的数目分别为n、n,vi、hj分别为显层第i个、隐含层第j个神经元的状态,它们对应的偏置分别为ai、bj;wij为显层第i个、隐含层第j个神经元之间的连接权重;设为RBM的参数;则RBM在状态(v,h)上的能量函数可表示为[14]:
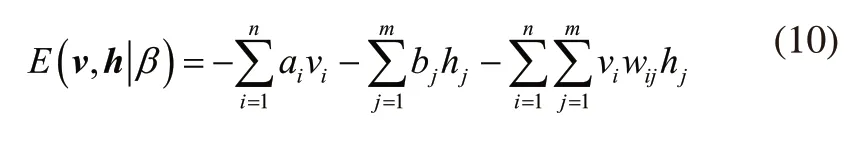
当显层单元向量v=(v1,…,vi,…,vn)随机给定后,隐含层第j个单元hj被激活的概率为:
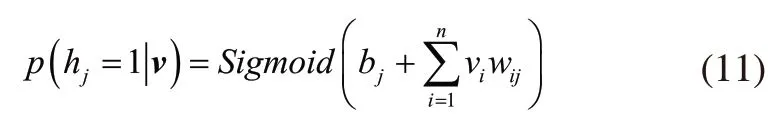
式(11)中,Sigmoid(x)=(1+e-x)-1为激活函数。
当隐含层单元向量h=(h1,…,hi,…,hn)随机给定后,显层第i个单元vi被激活的概率为:
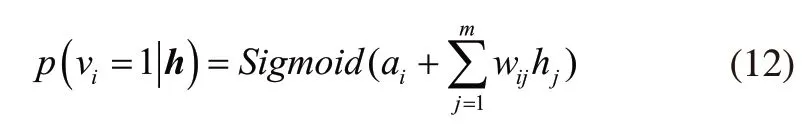
采用对比散度法(Contrastive Divergence,CD)[14]对RBM的参数β=(wij,ai,bj)进行寻优,选择一个样本作为显层的初始状态v;然后根据式(11)计算得出h;再根据式(12)计算隐含层神经元更新后的状态v'=(vi');再根据式(11)计算隐含层神经元更新后的h'=(hi'),更新公式为式(13):
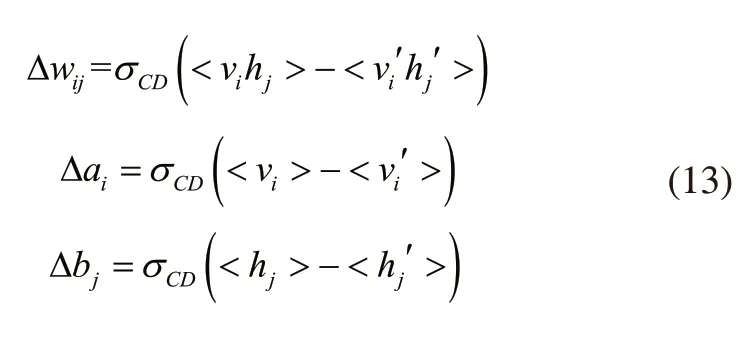
式(13)中,σCD为CD法的学习速率;<⋅>为变量的数学期望。
第二步根据BP算法进行反向微调,根据DBN的输出值反向更新其网络和权重。
3)将待测日的气象数据代入训练好的组合模型中,输出光伏发电最终的预测功率Pi。
2.3 基于SVM-DBN的光伏发电预测方法求解流程
本文方法的具体流程图如图2所示。
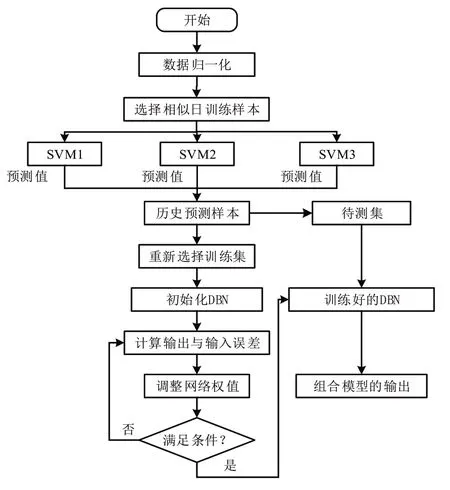
图2 本文方法流程图
3 实例验证
3.1 模型相关设置
本文数据来源于澳大利亚沙漠太阳能研究中心[15],将数据平均处理为每小时1个数据点,每天取08:00~18:00共11个数据点。选取2017年3月~5月和2018年3月~5月该地区光伏发电功率和天气数据作为原始数据。以天气平稳的2018-4-22和非平稳的2018-5-2作为待测日分别对模型进行测试。
最终的预测结果采用均方根误差eRMSE(Root Mean Square Error,RMSE)、平均绝对百分比误差eMAPE(Mean Absolute Percentage Error,MAPE)两个指标对预测模型进行评价,数值越小代表预测精度越高,其定义分别如式(14)、式(15)所示。
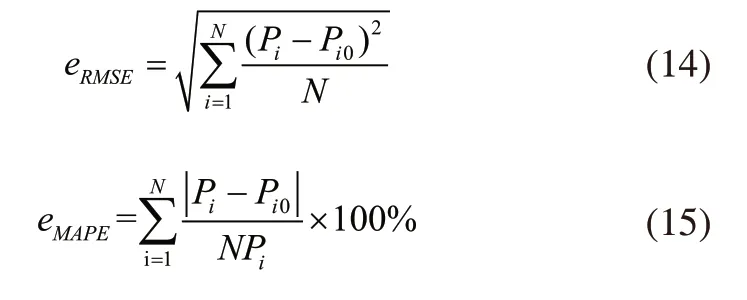
式(14)、式(15)中,Pi为预测功率值;Pi0为实测功率值;N为预测数据的个数。
本文SVM预测模型由LIBSVM改编而成,为了便于比较,除核函数外其余参数均采用固定的默认值。DBN中的隐层层数和单元数由枚举法选出最优值,经测试设置为双隐层结构,隐层单元数分别为3、11,DBN的学习率设为0.01,预训练和微调阶段的批量大小均设为5,预训练和微调阶段的迭代次数均设为250。
3.2 仿真结果分析
基于SVM1、SVM2、SVM3的预测模型和基于SVMDBN的预测模型的预测结果如图3、图4所示,将预测值和实测值代入式(14)、式(15)中得到对应的预测性能指标如表2所示。
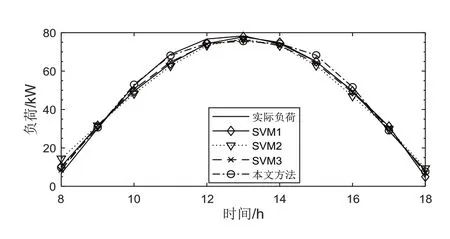
图3 2018年4月22日预测结果
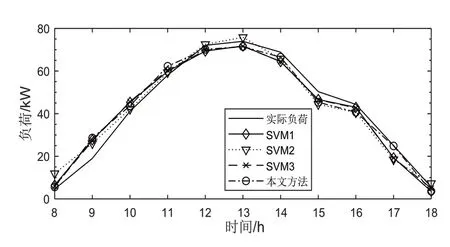
图4 2018年5月2日预测结果
由图3、图4及表2可知,两个待测日中本文方法的预测结果优于其他方法的预测结果。
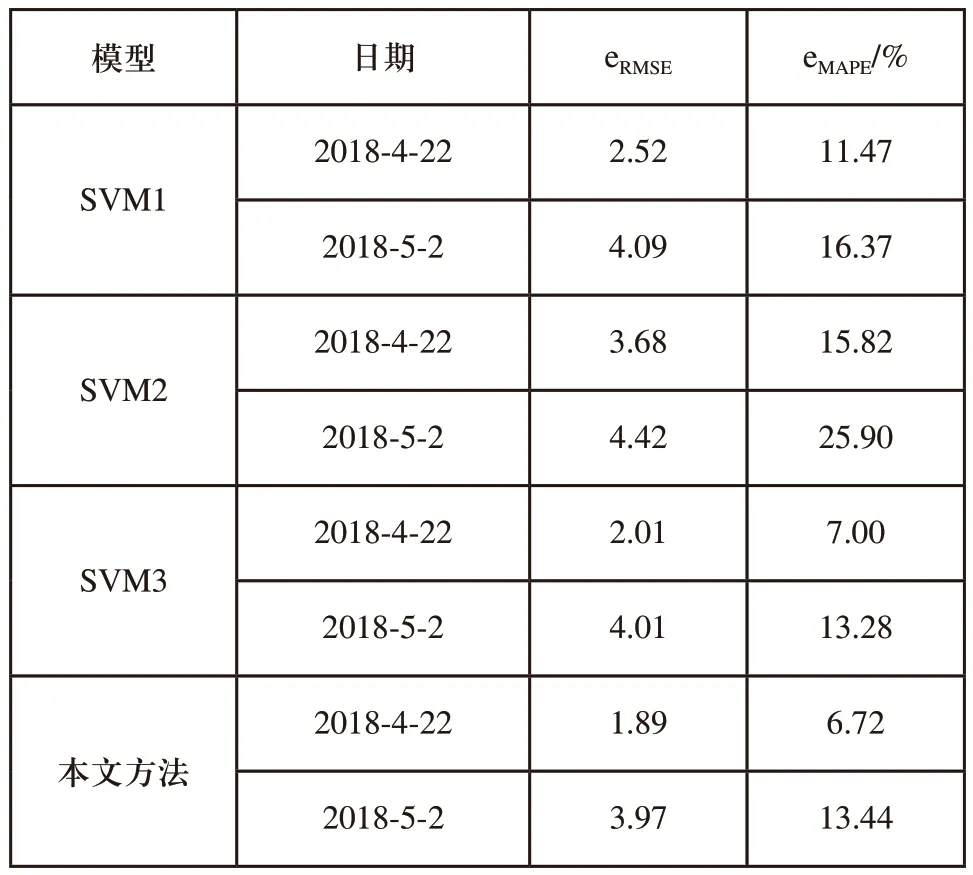
表2 不同模型预测结果对比
本文方法与其他文献方法的预测结果对比如表3所示。由表3可知,本文方法的预测结果优于其他文献方法的预测结果。
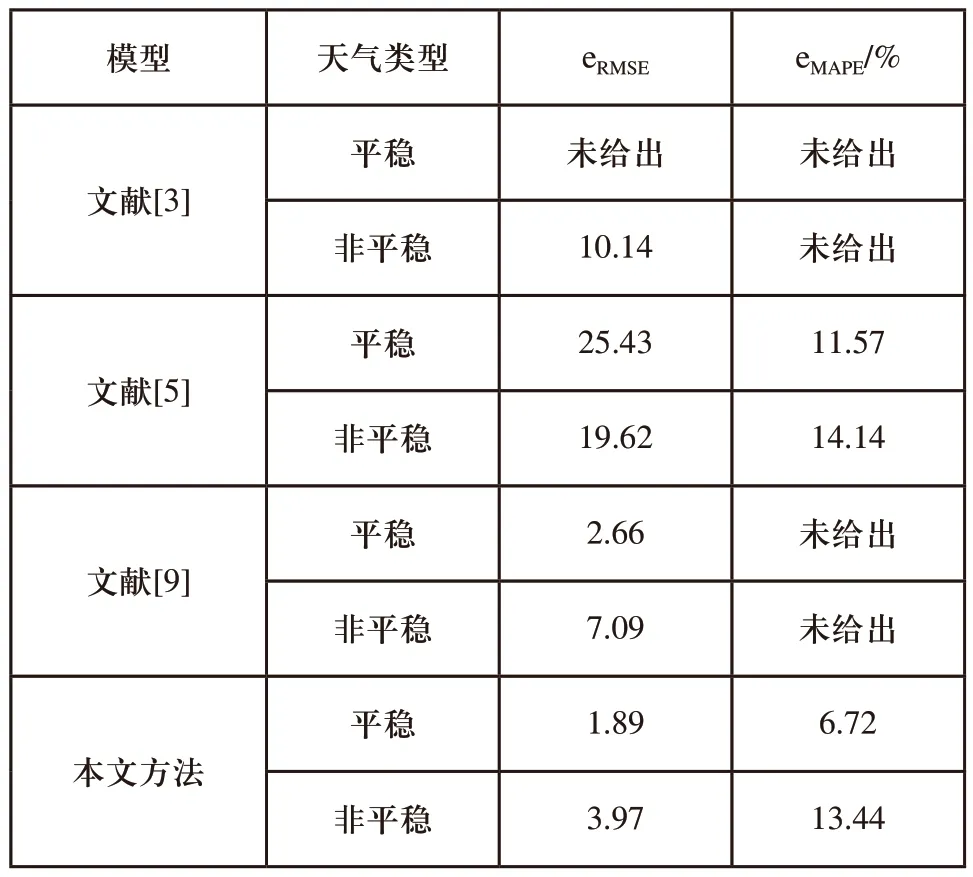
表3 不同文献预测结果对比
4 结论
1)采用改进的相似日算法对相似日进行选取,使得相似日的选择更加客观准确。
2)分别构建了基于三种不同核函数的SVM预测模型,证明了这三种单项模型进行组合预测的可行性,同时将这三种模型进行组合有效的解决了SVM受核函数影响的问题。
3)提出利用DBN对三种模型的预测结果进行权重分配,根据实际输出和期望输出的误差动态调整组合模型的权重,该方法根据三个单项预测模型的预测结果训练DBN来获得每一时刻的最优权重系数,使得权重的分配过程更为智能、客观、合理,克服了浅层模型的表征能力欠佳的缺点。
