光腔中两量子比特的量子关联动力学
2020-08-13白雪敏薛乃涛赵秀琴
白雪敏,薛乃涛,赵秀琴
(1.晋中学院,山西 晋中 030619;2.太原师范学院,山西 晋中 030619)
0 引言
非定域性是没有经典与之对应的量子力学最独有的特征之一.纠缠作为非定域性的一个典型例子,爱因斯坦、波多尔斯基和罗森都认为其是量子信息和量子计算的基本要素之一[1].一般来说,一个复合系统的纠缠态不能分解为两个量子态的直积状态.贝尔不等式(BI)的提出为非局部相关性的定量检验提供了可能.贝尔不等式(BI)的违反被认为是自然界最大的谜团之一,量子力学的研究从根本上改变了我们对微观世界的理解[2].近年来,BI的违背行为在理论上和实验研究上都引起了广泛的关注[3-4].据报道,许多有意义的实验已经证实了这一点.例如,BI的违反与量子力学预测相一致,纠缠的光子、被囚禁的离子和可转换的Josephson量子比特系统等等[5-7].不久之后,研究者把最初的BI形式推广到各种新的形式[8-9],其中一个更广泛引用的形式是由Clauser-Horne-Shimoni-Holt提出的CHSH不等式.在全同原子的光腔系统的纠缠和CHSH不等式被大量研究[10-11].最近,报道了一个利用金刚石中氮空位缺陷做的关于BI违反的无环实验[12].
尽管如此,目前的研究大多集中在静态纠缠的情况下.探索其动力学特性具有重要的意义.对于不同环境下双量子比特系统的量子关联的研究成为了热点问题[13-14].在本文中我们研究两个二能级原子与同一光腔相互作用系统的量子关联动力学问题.在 BI 违背中,我们从量子概率统计的角度重新推导了与模型相关的CHSH不等式.并探究了光场对两原子之间纠缠度的影响.
在第一节中,我们介绍了该系统的哈密顿量.在第二节中,推导出相关的CHSH不等式.在第三节,我们介绍了纠缠的相关定义.在第四节,我们探讨CHSH不等式、纠缠的动力学结果.最后,我们进行了讨论和总结.
1 物理模型以及含时演化密度算符
根据近期金刚石中含有氮空位缺陷实验中的贝尔不等式违背的研究[10-12],在本节,我们研究两个二能级原子与同一个光腔相互作用系统中CHSH违背动力学问题.在旋转波近似下,该系统的哈密顿量可以表示为H=H0+Hsf,其中
和
(1)
U(t)=
其中S=2a†a+1.
在Fock空间且基矢Λn={|+,+〉|n-1〉,|+,-〉|n〉,|-,+〉|n〉,|-,-〉|n+1〉}下,时间演化算符也可以写为
(2)
其中,
在这里关于时间的函数C1和C2分别为
在t时刻的态密度算符可以运用时间演化算符求出
ρT(t)=U(t)ρT(0)U†(t)
(3)
我们感兴趣的是场相互作用对量子相关的影响,因此假设初始态是一般的双自旋纠缠态
|Ψ(0)〉=sinφeiθ|+,-〉|n〉+cosφe-iθ|-,+〉|n〉,
(4)
接下来,我们把整个密度算符对光场求迹ρ(t)=TrfieldρT(t),可以得到两量子比特在标准基矢{|+,+〉,|+,-〉,|-,+〉,|-,-〉}下的密度算符矩阵形式
(5)
这里
我们注意到上面的矩阵形式为“X”态的形式,而且ρ14(t)=ρ41(t)=0,这种形式对CHSH不等式,以及纠缠的动力学研究都是特别适用的.
2 贝尔不等式的测量
BI是最早用来检测量子纠缠的判据之一,是通过定域性假设在经典统计学的基础上推导而来的.近年来,为了方便研究,贝尔不等式被人们扩展成各种形式的不等式.我们先考虑一个具有“X”态且ρ14(t)=ρ41(t)=0的量子态,这种情况下其密度算符可以被分成局域和非局域两个部分
(6)
这里局域部分可以写为:
(7)
非局域部分可以写为
(8)
纠缠态的两个量子相干分量可以导致贝尔不等式的违背.我们都知道两个自旋的贝尔测量分别沿着任意两个方向,例如方向a和b.在这两个方向下自旋算子的特征值分别为:
σ·a|±a〉=±|±a〉
和
σ·b|±b〉=±|±b〉,
通过求解上面的本征方程,我们可以得到对应的本征态如下:
和
它们通常被称为自旋南、北规范的相干态.n=a,b是两个由极化角度,在这里n=(sinθncosφn,sinθnsinφn,cosθn) 其中,θn和方位角度φn决定的单位矢量.两个自旋的测量输出结果可以写成两个自旋方向本征态的四种直积形式:
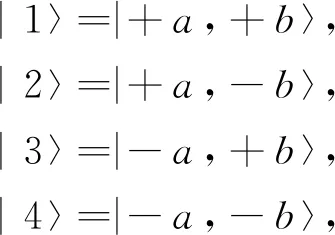
(9)
两个自旋在方向a和方向b的测量相关概率结果根据量子统计平均值得到的
P(a,b)=Tr[(σ·a)(σ·b)ρψ],
(10)
密度算符测量结果相关概率也可被分为局域部分和非局域部分
P(a,b)=Plc(a,b)+Pnlc(a,b),
局域部分产生a,b两个方向的贝尔关联
Plc(a,b)=(ρ11(t)+ρ44(t)-ρ22(t)-ρ33(t))cosθacosθb
(11)
和
ρtotal(a,b)=mcosθacosθb+nsinθasinθbcosθacosθb,
其中,m=ρ11(t)+ρ44(t)-ρ22(t)-ρ33(t),n=ρ23(t)+ρ32(t).
将这种贝尔关联式子带入由四个测量方向构成的量子CHSH关联概率式子中得到
PCHSH=|P(a,b)+P(a,c)+P(b,d)-P(d,c)|
(12)
接下来,我们回顾一下众所周知的CHSH不等式.它最初是由CHSH从经典统计学中局部性假设推导出来的,CHSH不等式适用于任意纠缠态的测量.只考虑局部时,
2|(ρ11(t)+ρ44(t)-ρ22(t)-ρ33(t))|,
(13)
当考虑非局部分时,当b⊥c,Φb=Φc,θb=0,θc=π/2,a=-d,P=(0,n/m,1),
(14)

3 纠缠
由文献[16]定义了瞬时纠缠并发度,它是一个众所周知两比特系统的纠缠的度量.
C(t)=max{0,Λ(t)},
(15)

最大CHSH量子关联与纠缠并发度进行比较,从而建立了CHSH不等式的违背与纠缠的动力学演化.
4 光场相干态下的量子动力学演化
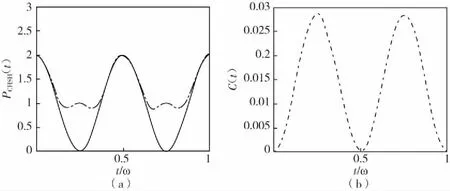
图1 量子CHSH概率黑色点虚线与黑色实线)和纠缠C(t)(图1-b中黑色虚线)随纲时间t/ω的变化规律其中角度参数,φ=0或π/2
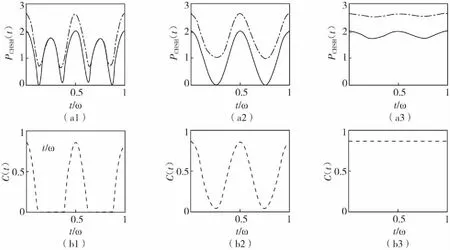
图2 量子最大CHSH概率黑色点虚线与黑色实线)和纠缠C(t)(图2-b1,图2-b2,图2-b3中黑色虚线)随纲时间t/ω的变化规律其中角度参数φ=π/6,而且θ=π/6(a1,b1),π/4(a2,b2),π/2(a3,b3)
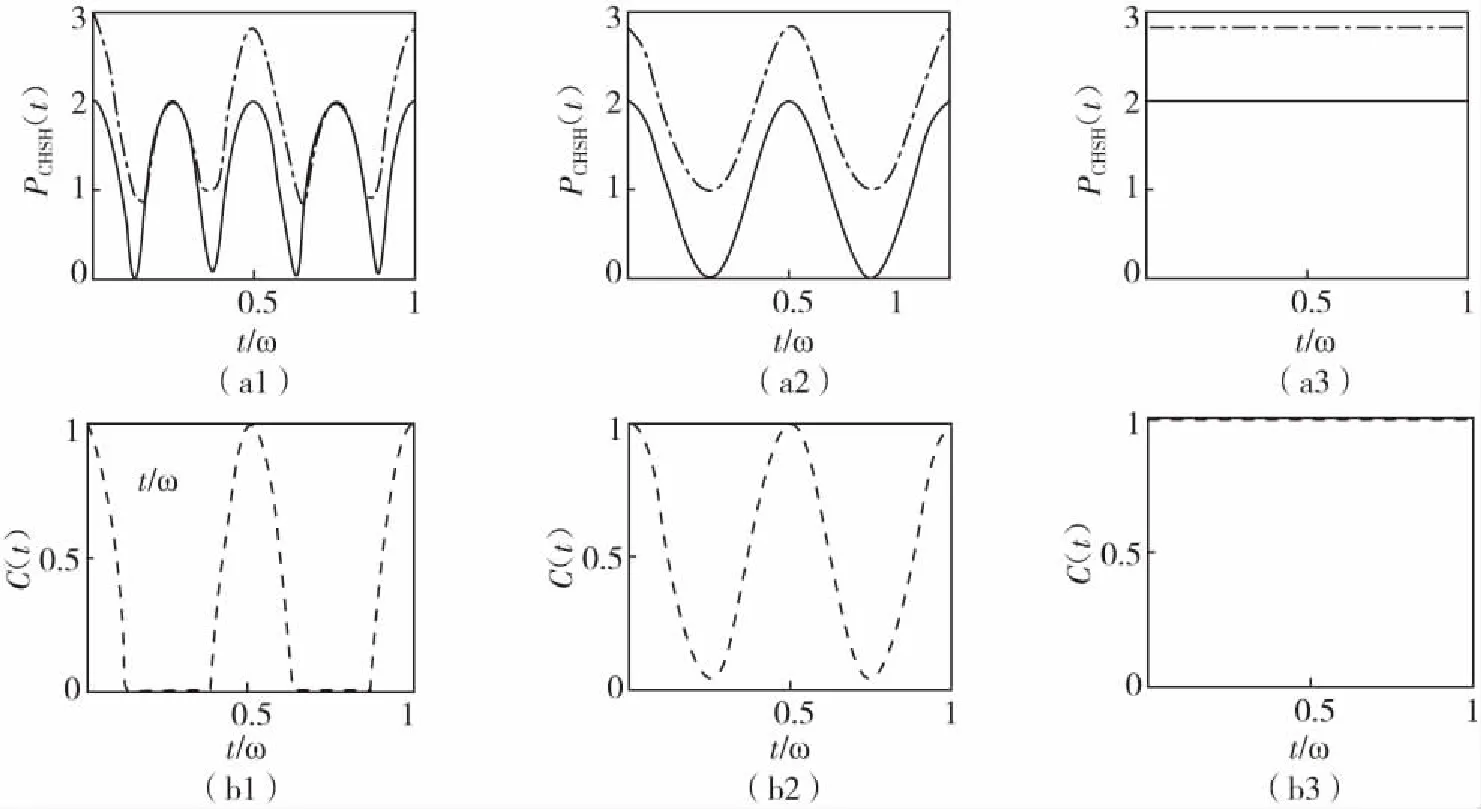
图3 量子最大CHSH概率黑色点虚线与黑色实线)和纠缠C(t)(图3-b1,图3-b2,图3-b3黑色虚线)随纲时间t/ω的变化规律其中角度参数φ=π/4,而且θ=π/6(a1,b1),π/4(a2,b2),π/2(a3,b3)
5 总结