再谈一道理想变压器动态分析的经典错题*
2020-08-13蔡志义
蔡志义
(漳州市第三中学 福建 漳州 363000)
1 引言
《物理通报》2018年第7期刊登了“经验让一个简单题目成为教师的一道经典错题——理想变压器的动态分析”一文,文中作者白红艳老师针对一道理想变压器动态分析的题目,指出一些有经验的教师用类比法来解决题目,虽能解出答案,但因为在类比过程中无形改变题干条件从而出错,紧接着她用严谨的数学推导证明此题答案.虽能让学生明白此题的来龙去脉,但耗时较多,故笔者也就此题谈谈自己的看法,用两种等效的思想方法解决此类问题,以期与白老师商榷及与同行探讨.
2 经典错题与解析
【例1】如图1所示为理想变压器,其中r为定值电阻,R为滑动变阻器,P为滑动变阻器的触头,u为正弦交流电源,电源输出电压的有效值恒定.则( )
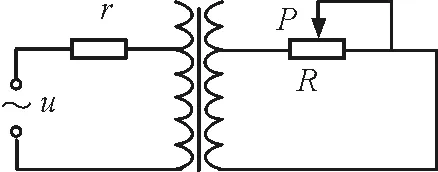
图1 例1题图
A.P向右移动时,原、副线圈的电流之比可能变大
B.P向右移动时,变压器的输出功率变大
C.若原、副线圈增加相同匝数,其他条件不变,则变压器输出电压不变
D.若原、副线圈增加相同匝数,其他条件不变,r消耗的功率可能不变
文献[1]的作者主要针对例1的选项B进行讨论,她指出有经验的教师用高压输电进行类比,当滑片P向右移动时,电阻增大,电流减小,功率减小,所以选项B错误.笔者认为有经验的教师应该会引导学生思考,这个选项在求解功率问题时,应当分为两种情况:一是定值电阻,二是变化的电阻.定值电阻由原来的分析没问题,但此题是滑动变阻器,它是变化电阻,不能按此思路分析,因为此时电阻和电流同时变化,由功率公式P=I2R知,此时功率的变化无法确定.讲到这里,学生就会明白可以与电源的输出功率进行类比,它有一个二级结论,当电源的外电阻与内阻相等时,输出功率最大.所以接下来用两种等效法(等效电阻法和等效电源法)解决此类问题.
(1)等效电阻法
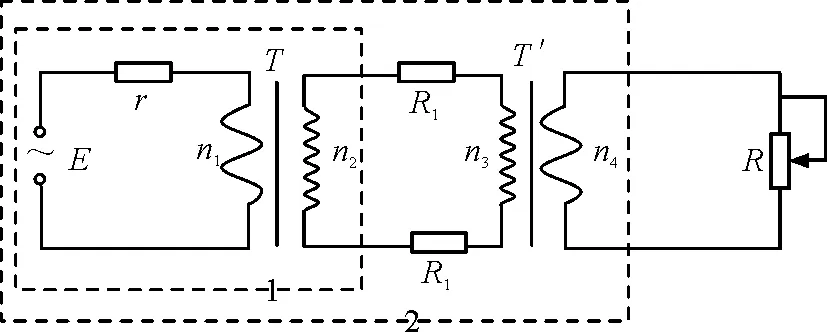
如图2所示,设输入电流为I1,输出电流为I2,原、副线圈的电压以及匝数分别为U1,U2和n1,n2.虚线框由一个R等等效替代,则
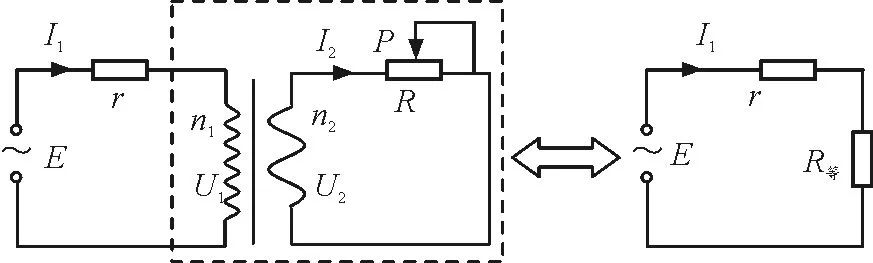
图2 等效电阻法图
E=U1+I1r
(1)
E=I1r+I1R等
(2)
U2=I2R
(3)
(4)
I1n1=I2n2
(5)
由式(1)~(5)得
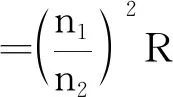
将r视为电源的内阻,由等效电阻法的结论得:
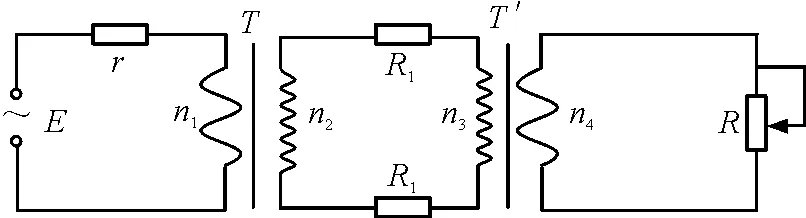
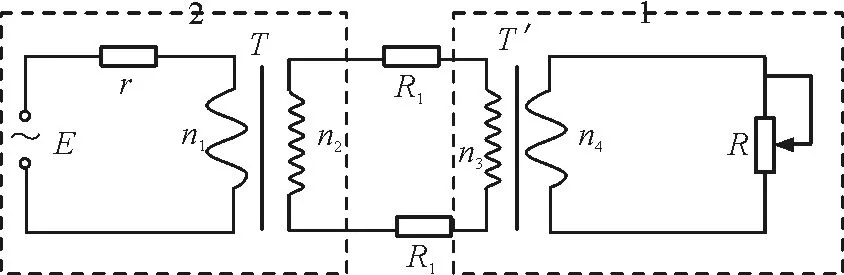
(1)若R等 (2)若R等≥r,则滑片P向右移动时,变压器的输出功率一直减小. (2)等效电源法 如图3所示,设输入电流为I1,输出电流为I2,原、副线圈的电压以及匝数分别为U1,U2和n1,n2.虚线框等效为一个新的等效电源,其电动势为E等,内阻为r等,则 图3 等效电源法图 E=U1+I1r (1) E等=I2r等+I2R (2) U2=I2R (3) (4) I1n1=I2n2 (5) 由式(1)~(5)得 由等效电源法的结论得: (1)若R (2)若R≥r等,则滑片P向右移动时,变压器的输出功率一直减小. 文献[1]通过大量繁琐的数学推导与分析得到变压器的输出功率是可能增大也可能减少,实则不然,更准确的结论是变压器的输出功率先增大到最大后减小,也可能一直减小.如果遇到更复杂的电路图,文献[1]的计算方法将更麻烦,而现在的学生应用数学解决物理问题的能力相对薄弱,就算计算出来,也要耗费相当长时间.对一道选择题来说,在保证正确答案的同时应尽量减少解题时间.下面,我们通过例2来分析应用这两种等效法在碰到更复杂的电路图时也可以高效解决. 【例2】如图4所示为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数为n1,n2.降压变压器T′的原、副线圈匝数为n3,n4.原线圈两端接入一电压e=Emsin(ωt)的交流电源,r为定值电阻,输电线的总电阻为2R1,R为滑动变阻器,不考虑其他因素的影响,则当滑动变阻器阻值为多少时,它的功率最大,最大值为多少. 图4 例2题图 (1)“等效电源法”解析 如图5所示,把虚线框1看作等效电源E等1,r等1 图5 等效电源法解析图 把虚线框2看作等效电源E等2,r等2 当r等2=R时,即 时,等效电源输出功率最大,滑动变阻器的功率有最大值,为 (2)“等效电阻法”解析 如图6所示,把虚线框1看作一等效电阻R等1 图6 等效电阻法解析图 把虚线框2看作一等效电源E等1,r等1 当R等1=r等1+2R1时,即 时,滑动变阻器的功率有最大值,为 如果例2用常规的计算方法求解,将耗费大量的运算时间,而且学生不一定能换算到最后一步,并需要用均值不等式来解极值.而用等效法能将复杂电路图进行简化从而大大减少繁琐的数学运算,提高解题速度,具有事半功倍的效果.另外,培养学生“等效法”的思想方法也具有重要的作用.还能对运用此思想方法的模型进行系统复习,如等效重力场等.
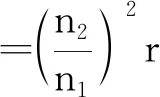
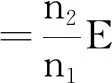
3 两种等效法的应用拓展