基于“STEM”理念下的“最速降线”探究
2020-08-13张金州
张金州
(长兴县太湖高级中学 浙江 湖州 313100)
1 概念的提出
“STEM”是科学(Science),技术(Technology),工程(Engineering),数学(Mathematics)4门学科英文首字母的缩写,其中科学在于认识世界、解释自然界的客观规律;技术和工程则是在尊重自然规律的基础上改造世界、实现对自然界的控制和利用、解决经济和社会发展过程中遇到的难题;数学则作为技术与工程学科的基础工具.
意大利科学家伽利略在1630年提出一个分析学的基本问题——“一个质点在重力作用下,从一个给定点到不在它垂直下方的另一点,如果不计摩擦力,问沿着什么曲线滑下所需时间最短.”尽管伽利略自己给出了“该曲线为圆”的错误答案,但是却为问题的解决指明了方向.在1696年瑞士数学家约翰·伯努利再次提出这个“最速降线”的问题并给出了正确解答,他还拿这个问题向其他数学家提出了公开挑战.最后牛顿、莱布尼兹、洛必达和伯努利家族的成员等解决了这个问题,求出的“最速降线”为旋轮线.
目前在中学阶段关于“最速降线”的问题仅为“谁先达到斜面底端”的简单问题求解与一些简单应用说明,而更高层次的研究与论述主要集中在“数学物理方法”层面,即仅在物理知识层面采用数学知识的阐述,这些阐述往往过于复杂,需要相当的数学知识才能有较为深刻的认识,而鲜有更系统性的分析以适应更多学习层次的论述.本文将从“STEM”理论的角度对“最速降线”问题进行探究.
2 基于“S”与“M”的分析
1696年,贝塞大学的伯努利提出了以下问题:如图1所示,在竖直平面内给定两点A和B,要寻找路径AMB,使得质点以最短的时间滑过该路径,假定质点的加速度仅仅来自重力作用,这就是有名的“最速降线”问题.通过数学物理方法得到其方程为
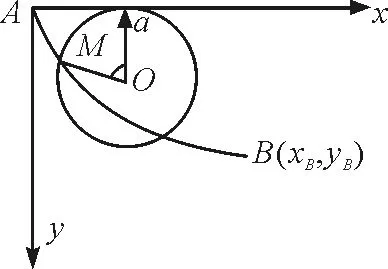
图1 最速降线问题示意图
x=a(θ-sinθ)y=a(1-cosθ)
(1)
式(1)即为“最速降线”问题的解,质点只在重力作用下沿此线下滑的速度最快、用时最短.其推导过程就不在这里推导了.
从科学与数学角度进行的分析与推导极为成功的获得了“最速降线”,但正处在中学阶段的普通学生将难以理解,因此,有必要将该问题进行合理简化的分析.
3 基于“S”与“M”的简化模型分析
“最速降线”的求解对于中学生来说要求较高,知识综合性较强,特别是其中涉及的数学运算;因此有必要将分析进行简化,成为一般学习能力的学生都可以探究分析的内容.现结合伯努利的思维方式和斯涅耳定律以寻求较为简化的模型分析[1].
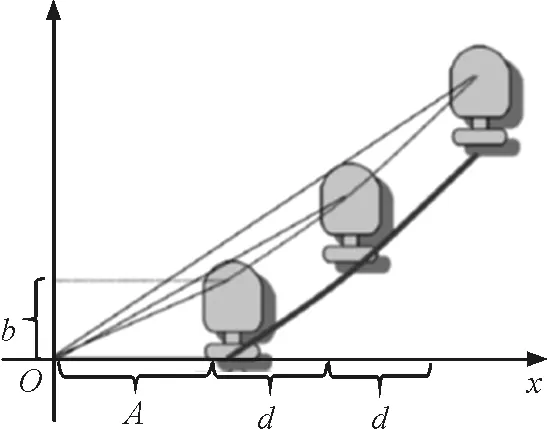
如图2建立坐标系,设A为坐标原点,B点坐标为(C,H),若用几个平行于x轴的带状区域将这一区域分成若干个小区域.小区域足够小,以至于物体在每个区域中的运动近似是匀速运动.根据机械能守恒定律,物体经过此区域时,其速度为
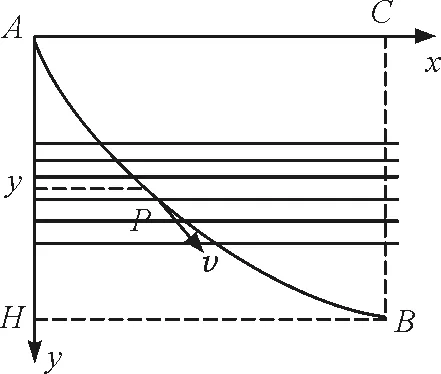
图2 “最速降线”简化模型
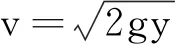
(2)
经不同区域的速度不同,从A到B运动的过程中速度是越来越大的.物体途经两个区域时速度不同,如图3所示.物体在区域Ⅰ中的运动的速度为v1,在区域Ⅱ中的运动的速度为v2.
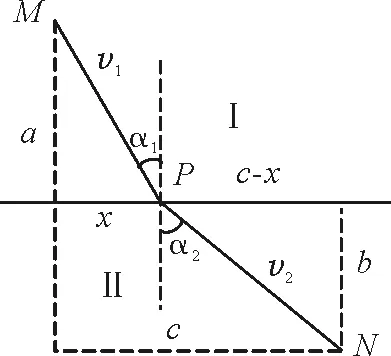
图3 “最速降线”物体运动过程中的速度区域划分
由几何关系可得
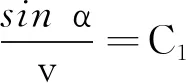
(3)
该结论与光的折射对应的斯涅耳定律是一致的.光入射到不同介质的界面上发生折射时,入射光和折射光位于同一个平面上,并且光在介质中传播的速度v与界面法线的夹角α满足如下关系
根据上述的相关特点便可以求“最速降线”方程了.如图4所示,设物体从A到B运动过程中任一位置纵坐标y对应的速度为v,v与y轴方向的夹角为α,与x轴方向的夹角为φ,则y′=tanφ,因而
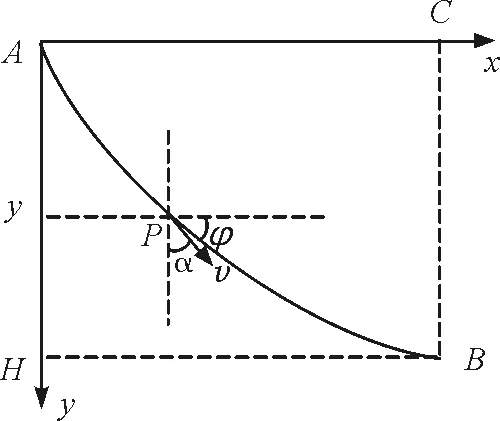
图4 物体运动过程中任一位置的速度分析
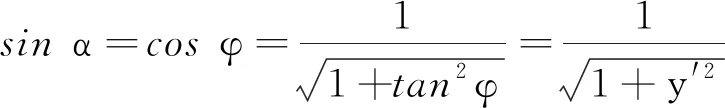
(4)
将式(2)~(4)联立可得
故y(1+y′2)=C,这就是旋轮线的微分方程.
将该微分方程转换为参数方程,上式可变为
令y=csin2φ,则
dx=c(1-cos 2φ)dφ
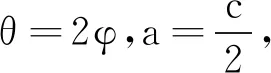
x=a(θ-sinθ)y=a(1-cosθ)
同样得到了“最速降线”的方程.
通过更加简化的推理分析模式,中学生基本上能用目前所学知识分析并理解“最速降线”问题,这有利于提高学生的认知.
4 基于“T”的验证
“最速降线”模型分析后还得通过技术手段进行验证,该验证从两个方面进行,即计算软件的验证和实验仪器的验证.
4.1 基于“T”的计算验证
沿着各曲线下滑的时间求解较为复杂,可以借助于一些专业的工具软件进行计算,本次计算采用的是Mathematica软件进行求解,在计算时间的程序编写中,引用文献程序,对方程进行求解[2].程序如下:
(1)由摆线可得沿摆线C1下滑的时间
如图1,从A(0,0)点运动到B(x1,y1),以下运动的A,B点相同,其中重力加速度取g=9.8 m/s2.
(β即为摆线中转过的圆心角)
编辑Mathematica程序如下:
g=9.8;x1=Input[];y1=Input[];
Print["x1="x1,",","y1=",y1]
t=FindRoot[(θ-sin[θ])/(1-cos[θ])=x1/y1,{θ,Pi}];
β=θ/.t;
a=x1/(β-Sin[θ])/.t;
T1=Sqrt[a/g]*β;
Print["β=",β]
Print["a=",a]
Print["T1=",T1]
运行该程序,先后输入x1=9,y1=4,程序运行结果为:
β=3.67631689,a=2.15006463,T1=1.72197031
(2)质点沿直线C2下滑的时间
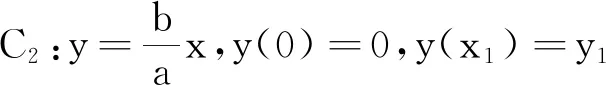
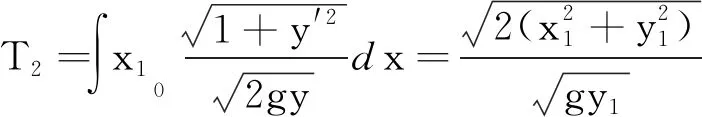
在上面的程序后面添加两条命令:
T2=Sqrt[2*(x1^2+y1^2)/g/y1];
Print["T2=",T2]
运行该程序,先后输入x1=9,y1=4,程序运行结果为:T2=2.22463
(3)质点沿圆弧C3下滑的时间
圆弧过A(0,0),B(x1,y1).则圆的参数方程C3(圆心应在x轴上):
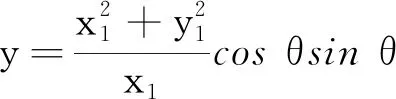
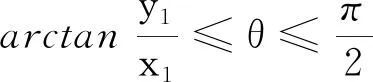
得
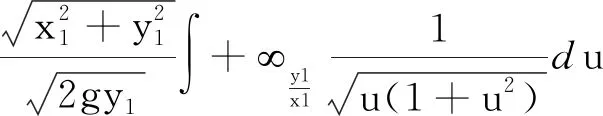
在上面的程序后面添加两条命令:
T3=Sqrt[(x1^2+y1^2)/2/g/x1]*Integrate
[1/Sqrt[u*(1+u^2)],{u,y1/x1,+}];
Print["T3=",T3]
运行该程序,先后输入x1=9,y1=4,程序运行结果为:T3=1.77911
(4)质点沿抛物线C4下滑的时间
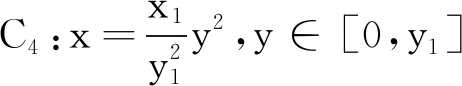
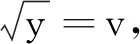
在上面的程序后面添加两条命令:
T4=Sqrt[2/g]/y1^2*Integrate[Sqrt[4*
x1^2*v^4+y1^4],{v,0,Sqrt[y1]}];
Print["T4=",T4]
运行该程序,先后输入x1=9,y1=4,程序运行结果为:T4=1.78157.
综合以上数据得如表1所示.
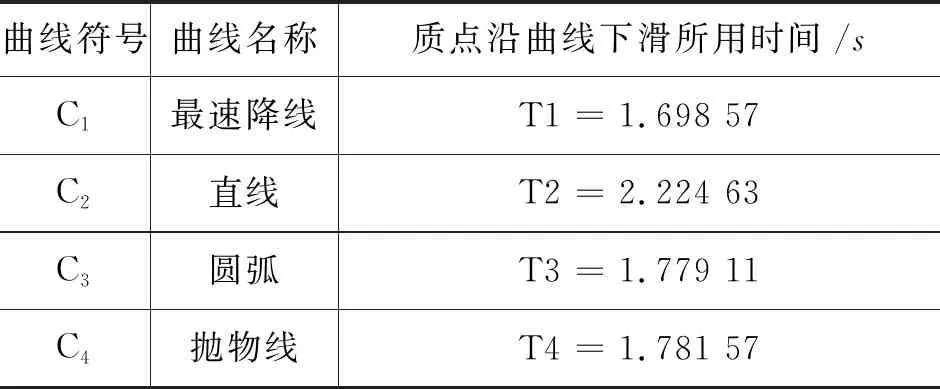
表1 曲线及对应时间
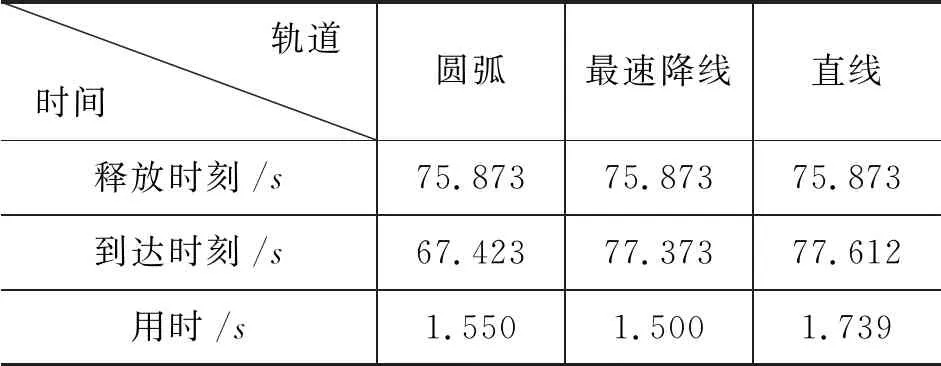
由表1可知,T1 理论分析后,还得通过实验进行验证.为此,准备了2个实验装置:科技馆的实验装置与自制实验装置. 科技馆的实验装置采用的是东莞市科学技术博物馆中的实验装置,其中有直线、最速降线、圆弧3条轨道和3个实验小球,如图5所示.实验时同时释放3个小球,通过录像记录慢速微调回放得到到达末端点所用时间,记录在表2中. 图5 科技馆的实验装置 表2 小球沿轨道运动的时间 由表2可知,小球3条轨道用时最少的是“最速降线”,其次是圆弧,用时最长的是直线;尽管“最速降线”用时最短,但非常接近圆弧用时. 在如图6所示的自制仪器实验现象中,依然可以观察到沿“最速降线”运动时间最短的情况(图6为手机慢拍模式截屏的情景). 图6 自制实验仪器 基于技术的计算软件和实验仪器两个方面的实际验证,可以发现质点沿着“最速降线”运动所用时间最短,这不仅直观,也更有说服力. 生活中还有许多现象与“最速降线”有关,尽管有些不是直观的“最速降线”,但原理实际上是类似的. “最速降线”在建筑中也有着美妙的应用.我国古建筑中的“大屋顶”,从侧面看上去,“等腰三角形”的两腰不是线段,而是两段“最速降线”.按照这样的原理设计,在夏日暴雨时,可以使落在屋顶上的雨水,以最快的速度流走,从而对房屋起到保护的作用,如图7所示.还有一些逃生系统都有类似的设计. 图7 我国古代建筑中的大屋顶 在影视厅或报告厅,经常会为前边观众遮挡住自己的视线而苦恼.显然,场内的观众都在朝台上看,如果场内地面不做成前低后高的坡度模式,那么前边观众必然会遮挡后面观众的视线,这也可以根据需要采用“最速降线”的情景模式进行分析与演算,从而满足各方面的需要而设计出最佳的座椅安排如图8所示[3]. 图8 “最速降线”应用于座椅安排演示图 杨秉烈先生发明了一种玩具叫做繁花曲线规,它由一套彩色塑料齿轮组成.一个大齿轮是环状的,牙齿做在里面;几个小齿轮的牙齿做在外面,小齿轮内部有一些小圆孔和几个其他形状的、较大的孔.使用时左手按住大齿轮,在大齿轮里放一只小齿轮,把笔尖插进小齿轮的某一个孔里,让小齿轮紧贴大齿轮内壁滚动,这时笔尖就会在纸上画出许多美丽的曲线花纹.若将大齿轮换成带齿的直尺,画出来的曲线就是“最速降线”,如图9所示. 图9 繁花曲线规 药物进入体内的方式有3种常见形式,即快速静脉注射、口服或肌注,医学上常用“房室系统”的观点来研究药物在体内的吸收、分布和排除过程,若能结合“最速降线”研究3种情况下体内血药浓度的变化曲线,将有助于得到血药浓度的变化,从而根据不同的疾病利用“药物动力学”找出最佳治疗方案[4]. 由于“最速降线”问题对大部分中学生而言过于困难,本文在“STEM”理念的基础上,从“S”与“M”的角度分析并简化了“最速降线”分析,从“T”的角度进行了计算验证与实验验证,最后从“E”的角度推广与拓展该模型,从中我们可以领略到该理念分析解决问题的强大能力——不仅可以更加系统、简便的研究、验证“最速降线”,甚至可以更高效地在生活中应用“最速降线”.4.2 基于“T”的实验验证


5 基于“E”的推广与拓展
5.1 “最速降线”应用在我国古代建筑中的大屋顶

5.2 “最速降线”还可以应用于影视厅或报告厅
5.3 “最速降线”规尺上的应用

5.4 “最速降线”在医学上的应用
6 结束语
