基于指数函数步长的果蝇优化算法

吴易轩 邓艳 廖淑珍 苏相琴

[摘 要]为了解决基本果蝇优化算法收敛速度慢、收敛精度低的问题，文章探讨基于指数函数步长的果蝇优化算法，该优化算法根据随机变化的搜索步长，设计指数函数自适应步长来代替原来的随机步长，基于7个基准函数D=30的测试，分析和比较新改进算法的迭代速度和搜索精度。实验结果表明，该算法具有更快、更稳定的搜索速度和更高的搜索精度，能够快速增加种群，解决种群多样性差的问题，并得到全局最优解。

[关键词]指数函数;果蝇优化算法;寻优步长

[中图分类号]G434 [文献标识码]A [文章编号]1008-7656（2020）04-0022-06

引言

群智能优化算法是近年来出现的一种优化方法。众所周知，求解各种特征优化问题的算法可以分为不同的类别。具有自然进化思想的启发式算法（Heuristic Algorithms）[1]在国内外学术界掀起了研究热潮。群体智能优化算法是模拟自然生物、人类社会等各种生物群体行为的结果。充分利用信息与合作，实现个体群体之间的优化目标。该算法原理具有结构简单、实现容易、效率高的特点。如遗传算法（Genetic Algorithm，GA）[2]、粒子群优化算法（Particle Swarm Optimization Algorithm，PSO）[3-4]、蝙蝠算法（Bat Algorithm，BA）[5]、蚁群算法（Ant Colony Optimization，ACO）[6]等。目前，群体智能优化算法作为一种基于群体智能的新型启发式算法，已应用于工程设计与制造、网络通信、自动控制、资源配置、远程教育等领域。

果蝇优化算法（Fruit fly Optimization Algorithm， FOA）[7-8]是学者潘文超在2011年提出的一种基于果蝇觅食行为的新型全局优化进化算法。与其他优化算法相比，果蝇优化算法具有算法简单、参数少、易于调整和优化精度高等优点。因此，越来越多的国内外学者开始研究该算法。目前，果蝇优化算法在很多方面得到成功的应用，如支持向量机故障诊断的优化[9]、自适应随机共振轴承故障信号检测方法的优化[10]、广义回归神经网络滚动轴承故障预测[11]等。基本的果蝇优化算法面临复杂性高、影响因素多、待解问题维度高等情况时，优化性能会显著降低。

由于指数函数增长的速度比较快，可很好地扩大果蝇个体的搜索步长，进而加快算法的收敛速度，并且能够有效地避免算法过早陷入局部最优。因此，将指数函数增长速度快的思想引入到基本的果蝇优化算法当中，本文提出一种基于指数函数步长的果蝇优化算法（A New Fruit Fly Optimization Algorithm Based On Exponential Function Adaptive Steps，EFOA）。在果蝇个体搜索求解过程中，增大寻优迭代的步长，其所产生的新个体有利于跳出局部最优，并且能够在搜索空间中找到潜在更优的解。

一、基本果蝇优化算法

果蝇优化算法通过模拟果蝇觅食的过程，得到果蝇优化算法的基本原理：首先是通过敏锐的嗅觉进行搜索的过程，利用敏锐嗅觉，分析空气中的食物源气味，判断气味源的大致方位，并向气味源飞行靠近。然后，通过视觉进行具体的定位，当飞近气味源并达到视觉的可视范围之内，迅速准确的判断食物的精准位置，并飞向食物。

模拟果蝇搜索食物的过程，将果蝇优化算法的数学模型，总结归纳为以下几个主要步骤。

步骤1，种群规模初始化Sizepop，迭代数的最大值Maxgen，果蠅群体的位置的随机初始化X_axis，Y_axis。

三、仿真实验

（一）实验仿真平台

操作系统：Microsoft Windows 7 旗舰版（32/Service Pack 1）;处理器CPU：Intel（R） Core（TM） i7-7700;机器主频：3.60GHz;内存（RAM）：8.00GB;集成开发环境：Matlab R2012（a）。

（二）测试函数

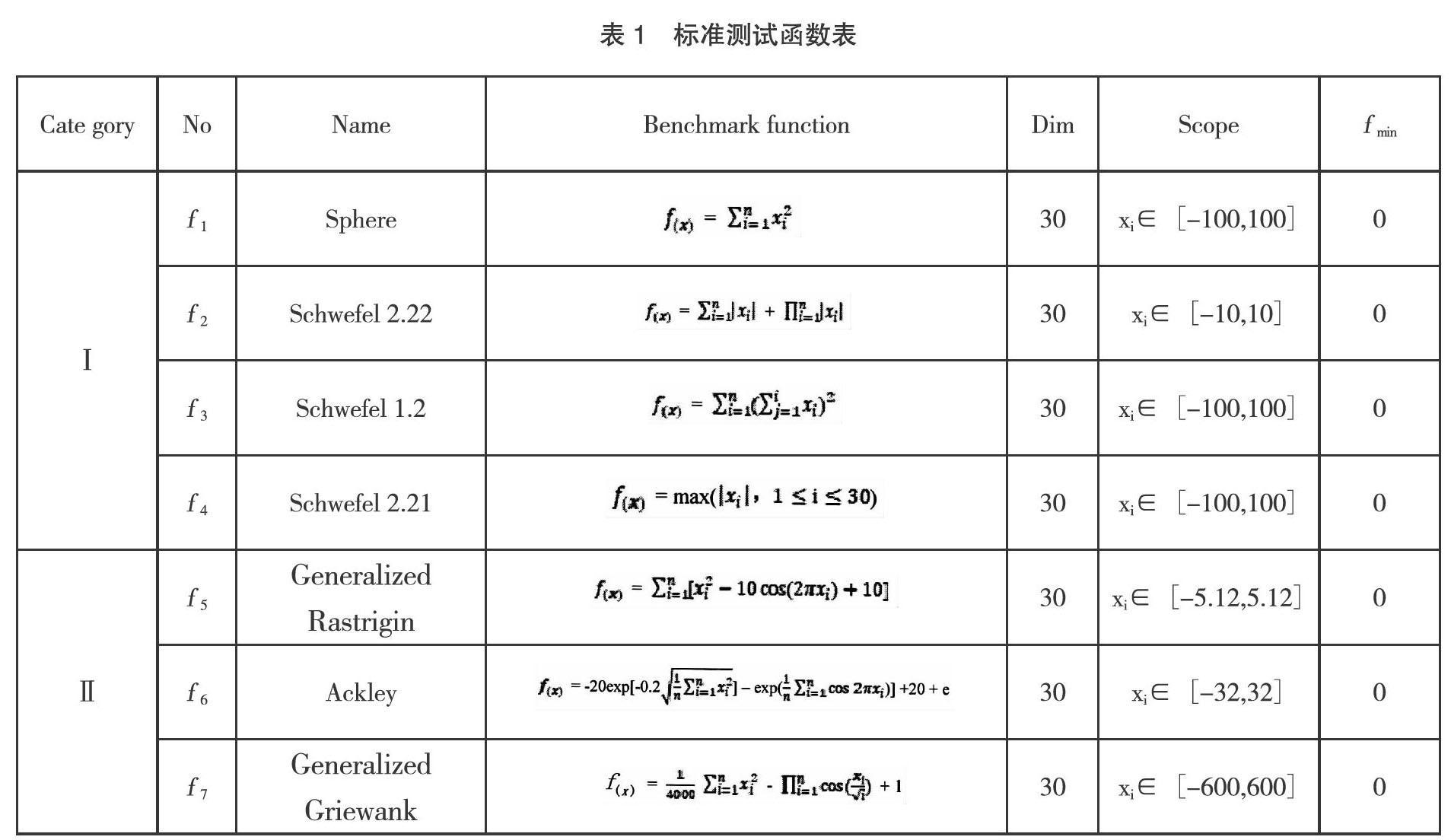
为了测试基于指数函数步长的果蝇优化算法性能的有效性，选取了在测试中使用广泛的7个标准测试函数[13]，利用这些测试函数对算法的性能进行检测。这7个测试函数均有不同的特点，单一某种算法不可能适用于全部的标准测试函数。使用这些函数进行测试，这样得到实验结果可以更能全面地反映算法的性能，更具有说服力。

本实验中，选取的测试函数各有特点，主要分为两大类：第Ⅰ类包括4个高维单峰函数f 1～f 4，第Ⅱ类包括了3个高维多峰函数f 5～f 7。表1列出了这些标准测试函数的名称、表达式、维数、自变量的取值范围以及算法在寻优时的理论极值。

（三）参数设置

文章提出的算法EFOA分别与其他5种群智能优化算法BA、CS、GGSA、MFO、FPA进行了对比测试实验，每个算法的最大迭代次数都设置为1000，种群规模设置为30，经过30次独立测试实验比较，算法中各项参数分别设置如下。

基本蝙蝠算法BA中，一般对参数如下设置：脉冲频率搜索范围为[0，2]，脉冲发射率的最大值R°=0.1，最大响度值A=0.9，响度衰减系数α=0.95，脉冲发射率增加系数γ=0.9，种群数为30。

在布谷鸟算法CS中，β=1.5， ρ 0 =1.5。

在GGSA算法中，G 0=100，α=20。

在基本的FPA算法中，参数设置交换概率ρ=0.8。

（四）实验结果对比与分析

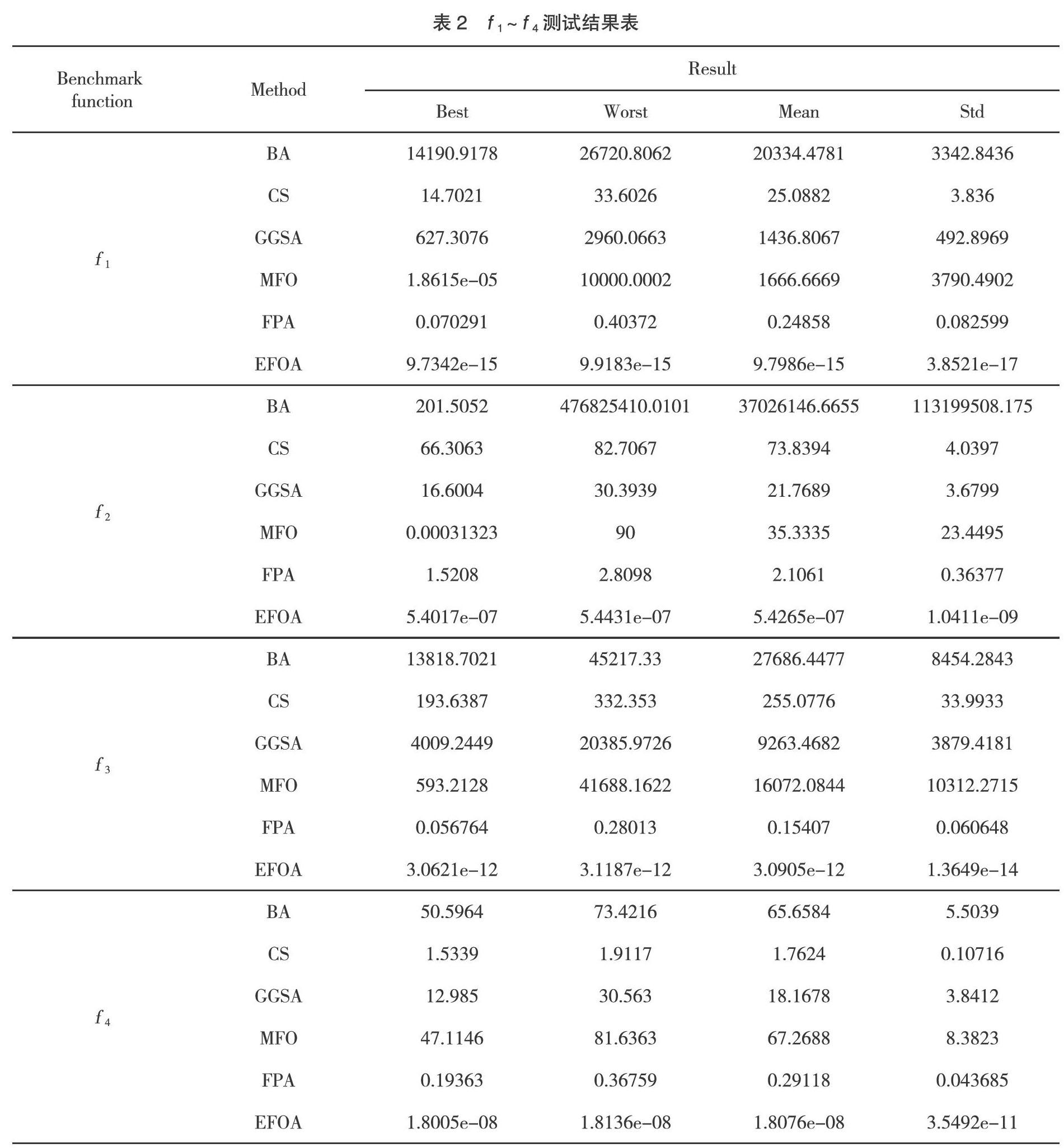
对表1中的两类标准函数分别独立进行30次测试，测试对比结果见下页表2和第26页表3。f 1～f 4为高维单峰函数测试，f 5～f 7为高维多峰函数测试，并对实验的结果进行对比试验。其中，表中的Best表示最优适应度值，Worst表示最差适应度值，Mean表示平均适应度值，Std表示标准方差值。其中，加粗字体的数据表示与其他算法进行比较时的最优实验结果，实验结果如表2所示。从表2实验结果对比分析可看出，在第Ⅰ类高维单峰函数测试中，指数函数步长的果蝇优化算法在求解此类5个函数时，EFOA算法与其他5种群智能优化算法在最优适应度值、平均适应度值、标准方差值对比中，均获得较大的优势，特别是在最差适应度值的对比中，EFOA算法的性能明显优于其他5种群智能优化算法。在函数f 1、f 2、f 3、f 4测试中，从6种群智能优化算法的对比实验结果可以看出，EFOA算法能够获得较大提高。f 1函数测试结果，EFOA算法最优值高于其他5种群智能优化算法最少高于10个数量级，最多高出20个数量级;f 3函数测试结果中，EFOA算法的最优值比最好的结果FPA算法高出10个数量级，比最差的结果BA算法提高16个数量级。f 4函数测试结果中，EFOA算法的最优值比最好的FPA算法高出7个数量级，相比最差的实验结果BA提高9个数量级。从标准方差的角度对比分析可以看出，EFOA算法的精度值均在10个数量级以上，表现出了此算法具有极高的稳定性。特别是f 1函数的测试结果，EFOA的标准方差值达到了17个数量级，明显优越于其他5种优化算法的标准方差值。在f 2函数的测试中，EFOA算法也表现出了很好的稳定性。对于多维单峰标准函数的测试结果，EFOA均表现出了其算法的优越性、稳定性、鲁棒性。因此，EFOA在高维单峰情况的最优解和稳定性明显优于其他5种算法，具有一定的优势。

从表3的实验结果对比来看，EFOA算法在高维多峰中的表现也十分优异。在寻优精度值方面，EFOA算法表现出了较高的精度，特别在函数f 6、f 7的函数测试结果中，EFOA比其他5种优化算法表现出了较高的精度值。在函数f 6的测试结果中，EFOA算法的求解精度比最好的MFO算法提高5个数量级，比最差的BA算法提高9个数量级;在函数f 7的测试结果中，EFOA算法的求解精度比最好的MFO算法提高9个数量级，比最差的BA算法提高16个数量级。在第Ⅱ类高维多峰函数测试结果中，EFOA算法的标准方差结果均优于其他5种优化算法。显然，对于第Ⅱ类函数，EFOA的稳定性优于其他5种优化算法。进而说明了EFOA算法具有更强的鲁棒性、更好的稳定性、较好的可移植性。

四、结论

针对基本果蝇优化算法种群多样性差、寻优精度较低、容易陷入局部最优、求解收敛速度慢以及高维搜索性能较差等不足，将指数函数增长步长融入到果蝇优化算法中，提出了一种基于指数函数步长的果蝇优化算法，利用指数函数增长速度快，提高了算法的搜索速度;利用指数函数以增大寻优迭代的步长，可以有效避免算法陷入局部最优，有利于迭代所产生的新个体跳出局部最优，达到全局搜索最优值。仿真实验结果表明，基于指数函数步长的果蝇优化算法是有效、可行的，并且在求解高维单峰、高维多峰函数时表现出良好的性能。

[参考文献]

[1] Yu-Yu Zhao， Xin-She Yang， Li-Qiang Liu， Emerging Meta-heuristic Algorithms. science Publishing， 2013.

[2] K. S. Tang， K. F.Man ， S.Kwong，  and Q. He， “Genetic algorithms and their applications，” IEEE Signal Processing Magazine， vol. 13，no. 6， pp. 22-37， 1996.

[3] J. Kennedy，“Particle swarm optimization，” in Encyclopedia of Machine Learning， C. Sammut and G. I.Webb， Eds.， pp. 760-766， Springer US， 2010.

[4] Kennedy J， Eberhart R. Particle swarm optimization， in Neural Networks， 1995.In： Proceedings， IEEE international conference on; 1995. p. 1942-1948.

[5] Cheng L I. A New Metaheuristic Bat-Inspired Algorithm， Nature Inspired Cooperative Strategies for Optimization （NICSO 2010）. Springer Berlin Heidelberg， 2010：65-74.

[6] Dorigo M， Blum C. Ant colony optimization theory： A survey[J]. Theoretical Computer Science， 2005， 344（2-3）：243-278.

[7] Pan W T. A new Fruit Fly Optimization Algorithm： Taking the financial distress model as an example.

Knowledge-Based Systems， 2012， 26（2）：69-74.

[8] Wang L， Zheng X L， Wang S Y. A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem. Knowledge-Based Systems， 2013， 48（2）：17-23.

[9] 牛培峰， 麻紅波， 李国强，等. 基于支持向量机和果蝇优化算法的循环流化床锅炉NOx排放特性研究[J]. 动力工程学报， 2013（4）.

[10] 崔伟成， 李伟， 孟凡磊，等. 基于果蝇优化算法的自适应随机共振轴承故障信号检测方法[J]. 振动与冲击， 2016（10）.

[11] 付岩. 果蝇算法优化的广义回归神经网络滚动轴承故障预测[D]. 哈尔滨：哈尔滨理工大学，2018.

[12] 曹建军.“指数函数的图像和性质”的探究学习——基于信息技术与建构主义的数学实验教学案例[J]. 教学月刊：中学版， 2003（10）.

[13] Jamil M， Yang X S. A Literature Survey of Benchmark Functions For Global Optimization Problems[J]. International Journal of Mathematical Modelling & Numerical Optimisation， 2013， 4（2）：150-194.

[作者简介]吴易轩（1987-），男，河南周口人，广西广播电视大学教师，硕士，研究方向：智能优化及应用;邓艳（1979-），男，广西南宁人，广西广播电视大学高级工程师，硕士，研究方向：建筑电气工程与管理;廖淑珍（1984-），女，广西南宁人，广西广播电视大学教师，硕士，研究方向：计算机软件、区块链应用技术;苏相琴（1984-），女，广西北海人，广西广播电视大学高级工程师，硕士，研究方向：遥感与地理信息技术研究。

[责任编辑 刘绍英]