基于PCA 和K-Means 聚类的医疗物资分配模型
2020-08-12李颖杰
李颖杰
(重庆交通大学,重庆400074)
为了给各地区物资稀缺程度评级,首先通过分析发现影响一个地区物资紧缺程度的因素主要有该区域的总人口、新确诊肺炎人数、区域医院数量、区域医护人员数量、区域医疗设备生产厂数量和区域的GDP。下面先对这些数据进行预处理,并进行主成分分析。
1 主成分分析
首先,由于指标的大小差异很大,对原始数据进行了归一化,使每个指标处于相同的数量级。采用标准差标准化法,即:
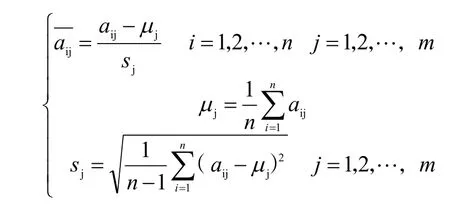
与此相对应,以下称为标准化指标向量:

考虑到上述指标间还可能存在着一定的相关性,为了更精准地分析影响地区物资紧缺程度的指标,使用了主成分分析法对指标数据进行了标准化处理,用尽可能少的主成分来代替原来的变量,同时又使保留的主成分具有与原数据相同的信息。
主成分分析步骤如下:
第一步,计算相关系数矩阵:
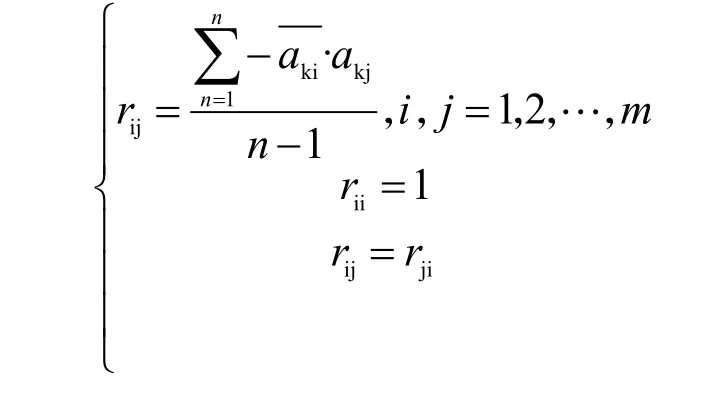
第二步,计算相关系数矩阵Rλ的特征值λ1≥λ2≥…≥λm≥0 以及相应的特征向量μ1,μ2,…,μ6,从特征向量中组合m 个新的索引量:
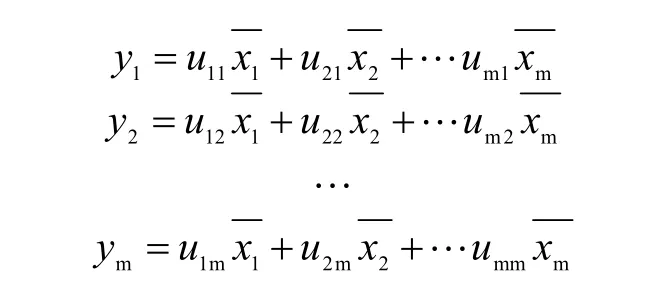
第三步,计算特征值λj(j=1,2,…,6)的信息贡献率和累积贡献率。主成分yj的信息贡献率bj的公式如下所示。主成分yj的累积贡献率αp公式如下所示。当αp的取值接近于1(一般取值为0.85、0.90、0.95)时,则选择前p 个指标变量y1,y2,…,yp作为p 个主成分,以此来代替原来的6 项指标。
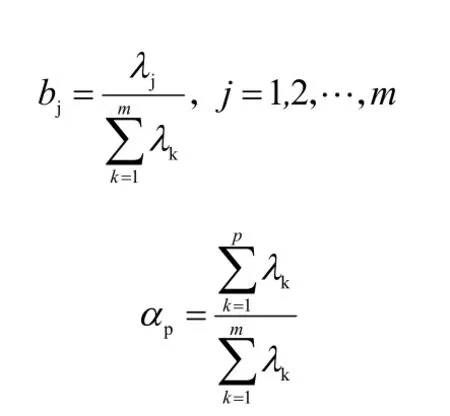
通过上述分析,我们确立了p 个主成分,这p 个主成分互不相关,并且保留了原始数据的基本信息。
2 确定最佳聚类数
确定聚类的最优数量对聚类的有效性有很大的影响,使用相同的聚类算法来评估不同聚类条件下聚类结果的指标优度。内部指标有三类:基于数据集模糊划分的指标、基于数据集样本结构的指标和基于数据集统计信息的指标。基于数据集几何结构的指标是根据数据集本身的统计特征和聚类结果来评价聚类结果,并根据聚类结果选择最佳的聚类数。根据K 均值聚类方法的原理,选择Davies-Bouldin 指数进行评价。
DB指数是通过描述样本的类别散度和类别中心之间的距离来评估的,DB越小,类之间的相似性越低,聚类效果越好。定义如下:
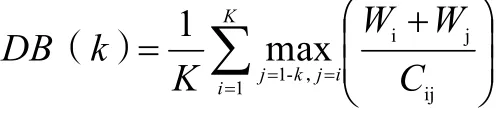
确定最优聚类数应首先给定K的范围(给定K范围为0~9),在数据集上使用不同的聚类数K运行相同的聚类算法,得到一系列聚类结果,并计算每种聚类数的DB值,结果如图1 所示。分析图1 结果,选择了最佳聚类数为4 个类别。

图1 DB 值计算结果
3 K-Means 聚类分析
K-Means 聚类算法是聚类算法中最广泛应用的一种算法,易于实现,效率高。下面对湖北各地区的物资紧缺程度进行K-Means 聚类分析。
记湖北各地区的特征向量为a1,a2,…,am,按照如下步骤聚类分析。
Step1,选择初始的k个类别中心u1,u2,…,uk。
Step2,对于剩余的每个特征向量,将其归类到距离最近的类别中心的类别,即
Step3,将每个类别中心更新为隶属该类别的所有样本的均值,即,cj为第j个类别的集合。
Step4,重复Step2、Step3,当j值为4 时,停止运算。
4 结果
在问题的求解中,本文主要用到了湖北各区域的总人口、新确诊肺炎人数、各区域医院数量、各区域医护人员数量、各区域医疗设备生产厂数量和区域的GDP 等数据来刻画某区域的物资紧缺程度。在求解中,首先通过计算DB的值选取了最佳聚类数——4 类,从而通过K-Means 聚类法将把湖北各地区的物资紧缺程度划分为四个等级,划分的结果如表1 所示。

表1 湖北各地区物资紧缺程度
我们应给物资紧缺程度高的地区分配更多的医疗物资,根据以上的聚类结果,结合实际情况制定了物资分配方案,如表2 所示。
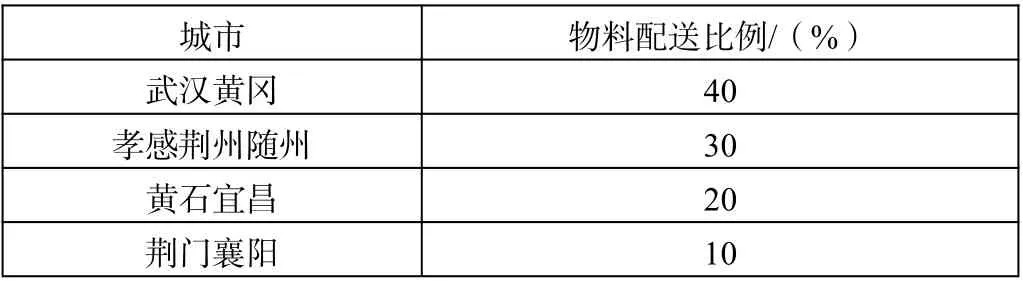
表2 物资分配方案
5 结语
通过对湖北各地区指标的主成分分析以及K-Means 聚类,将湖北各地区的物资紧缺程度分成了四个等级,并制定了可行合理的物资分配方案,这对湖北地区的物资分配问题有较大的参考价值。同时,本文将Davies-Bouldin 指数与K-Means 聚类法结合的模型还可以推广到更多的领域,对我们处理大数据和指标分类有重要的意义。
