基于时间序列模型的RED算法研究

2020-08-12李多佳

互联网天地 2020年7期

□ 文李多佳刘静许勇

一、引言

RED算法曾是一种有效的网络拥塞控制算法，其主要思想是通过路由器输出端的队列长度控制发送端的数据。算法操作简单易实现，但同时也存在着参数难以确定、难以有效处理突增的网络流量以及公平性等问题。随着网络信息量的爆炸式增长，现行RED算法已经无法有效解决网络流量过分饱和的现状，也无法保证网络的服务质量。很多学者针对RED算法的缺陷展开了优化，基于数学方法提出了对丢包率的改进公式，降低了参数的敏感性，避免了概率突变的问题。本文基于时间序列模型对RED算法展开研究，首先建立时间序列模型，对已收集的网络流量数据进行归一化处理；对归一化处理后的样本进行训练直至达到精度要求，得到科学的模型参数；再设置预测值，计算出预测流量的平均队列长度。在此基础上，结合RED算法，得到合理的数据包丢包概率，动态调整平均队列长度，控制网络中的数据包传送。

二、国内外研究现状

RED算法由Sally Floyd和Van Jacobson首次提出，通过随机选择分组进行丢弃或标记，在队列溢出之前降低数据的发送速率，以缓解网络拥塞。后来，一些学者提出了各种改进的RED算法来提高网络性能。其中包括运用非线性公式增强算法中丢包概率的计算，用平滑的概率曲线替代振荡的概率曲线，借鉴Sigmoid函数的特性，在参数设定上降低了难度，避免了丢包概率突变的发生；基于流量预测的改进RED算法，利用人工神经网络模型进行流量预测，同时综合模拟退火和粒子群算法进行改进，进一步完善RED算法；Adaptive RED(ARED)算法，运用统计复用的方法，通过检查平均队列长度来调整发送窗口大小；DyRED算法，使用一个动态的最大阈值来控制路由器缓冲区在溢出之前的早期阶段的拥塞，进一步减少丢包，提高吞吐量；基于自适应动态调整的RED算法，利用S型升半哥西分布函数对丢包率函数进行非线性处理，利用目标队长的范围和平均队列长度的关系引入参数自适应调整策略对最大丢包率进行改进；建立基于一维离散时间的路由器网络拥塞控制非线性模型，通过对数据包丢包概率的参数进行控制，解决了参数的低维混沌问题，提高了算法的稳定性；QARED算法的改进，通过改变丢包概率计算函数，进一步提高了算法的自适应性、稳定性，降低网络丢包率；利用频时交替半解析法（HB-AFT)，研究了延迟非光滑网络TCP-RED拥塞控制系统周期解的近似解析表达式，提出了具有时滞的非光滑动力系统周期解的精确近似解析表达式；Smart-RED算法，使用平均场模型，解决了突发UDP流量或TCP连接时可能出现的问题，保持了较低的队列大小和合理的带宽利用率，缓解了网络拥塞。

目前已有的改进RED算法在实际应用上仍存在着参数难以选定、队列长度震荡不定等问题，本文在RED算法的基础上，考虑到网络流量具有自相似性、长相关性、周期性、混沌性等特征，提出了一种基于时间序列模型预测流量的RED拥塞控制算法（ARIMA_RED），采用统计、数学等方法结合实际情况确定RED算法的参数，处理网络流量突增问题，在缓解网络拥塞中具有一定效果。

三、基于时间序列预测流量的RED拥塞控制算法——ARIMA_RED算法

3.1 ARIMA_RED算法原理

本文通过建立ARIMA模型来对流量值进行预测，归一化处理网络流量训练集数据，首先计算出瞬时队列长度与平均队列长度，再以平均队列长度作为RED算法的输入参数来动态控制丢包率，控制网络中的数据包传送。

3.1.1 ARIMA模型

ARIMA模型是时间序列中的一个重要模型，基本思想是把需要进行预测的序列看成为随机序列，在此基础上不断计算并寻找最适合描述数学模型。当建模成功后，将已有的数据作为历史输入，经过模型计算输出预测值。

3.1.2 ARIMA模型流量预测

在使用ARIMA模型预测网络流量前，首先要对抓取的网络流量数据集进行数据预处理，将预处理后的数据通过ARIMA模型进行检验，以此来判断模型是否具有数学意义。具体步骤如下：

（1）检测序列的平稳性。以ADF单位根检验网络流量预测模型的散点图、自相关函数、偏相关函数图的方差、趋势。

（2）平稳化处理。网络流量具有突发性、实时性，所以网络流量的时间序列模型基本为非平稳模型，存在变化的趋势，此时，需要通过差分处理来处理数据。当网络流量存在异方差时，必须通过技术手段处理数据。当处理后的数据具有自相关函数值和偏差时，说明经过处理的数据序列已为平稳序列，可以作为模型的输入数据。

（3）建立模型，通过估计参数来判断模型的建立是否具有数学意义。本文通过wireshark软件抓取的流量经过时间序列分析得出其偏相关函数与自相关函数在函数图上均为拖尾，故本文选取ARIMA模型来处理数据。

（4）使用建立好的ARIMA模型预测流量。

（5）将预测出的瞬时流量值作为ARIMA_RED算法的输入参数，代入ARIMA_RED算法的计算公式，经过计算得出路由节点的丢包率p。

ARIMA模型流量预测流程图如图1所示。

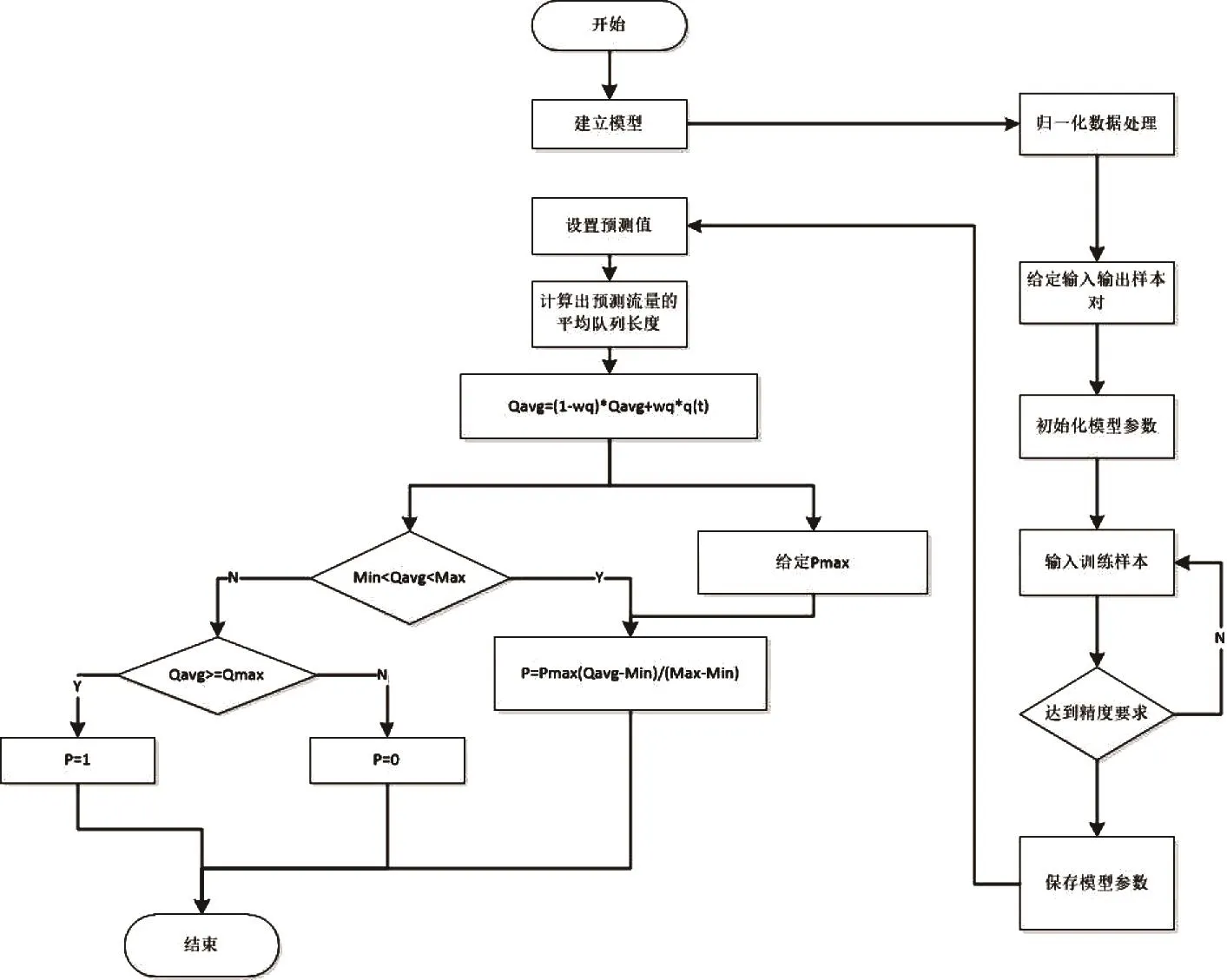
图1 ARIMA_RED算法流程图

3.1.3 ARIMA_RED算法步骤

ARIMA_RED算法伪码描述如图2所示。

其中参数q为当前队列的长度；time为时间；q_time表示队列最初空闲时间；m路由器在空闲状态下发送的最小报文数；f(t)为t的线性函数；count是自从最后一个数据包被丢弃以来已收到的数据包数；timeseries( )为时间序列模型数据处理； A RIMA( )为预测算法。

3.2 时间序列模型预测评估

本文利用wireshark软件抓取了一定时间内某网络的数据包个数以及出现错误的情况，作为ARIMA模型的输入参数，数据集如表1所示（数据集过长，此处只选取前十列）。

图2 ARIMA_RED算法伪码

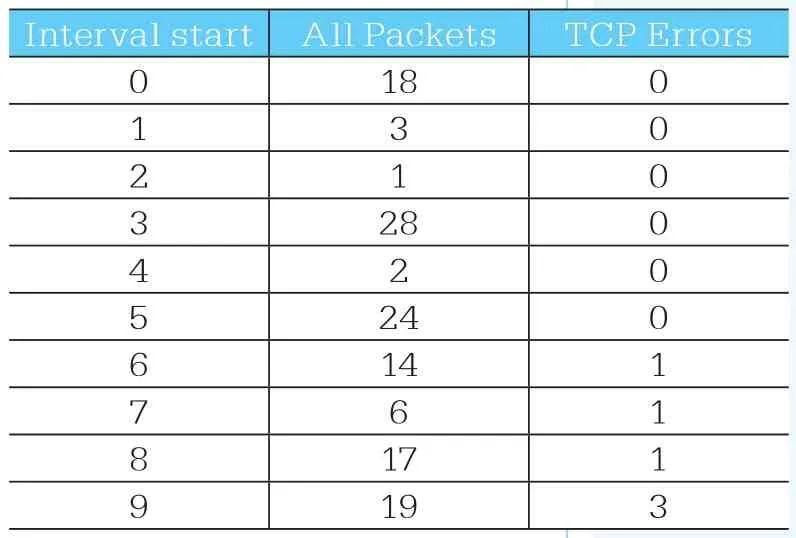
表1 部分时间序列模型数据集

接着利用ARIMA模型进行建模分析，得出的结果如表2所示。

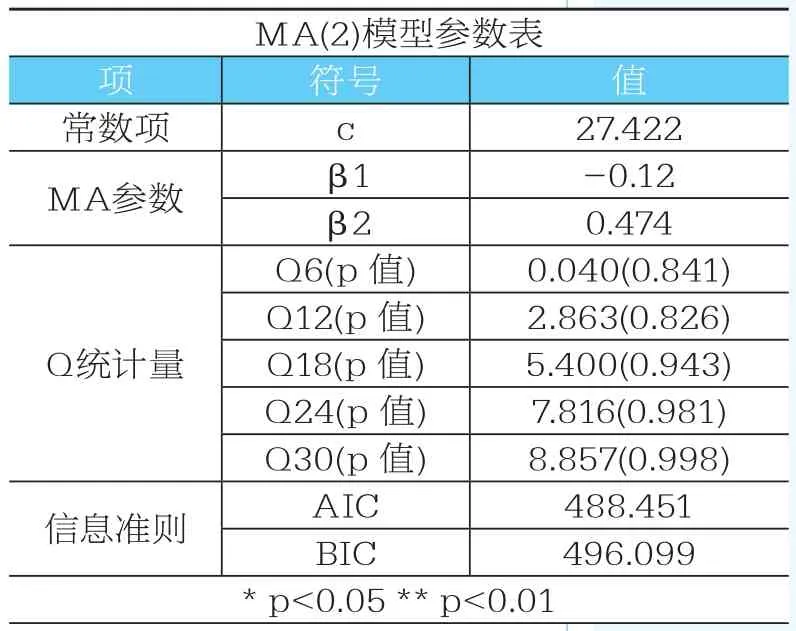
表2 ARIMA模型建模结果

针对表2的数据，在数学意义上结合AIC信息准则，软件自动对多个潜在备选模型进行建模和对比选择，最终找出最优模型为：MA(2)，其模型公式为：

从Q统计量结果看，Q6的p值大于0.1，则在0.1的显著性水平下不能拒绝原假设，模型的残差是白噪声，模型基本满足要求。

图3 时间序列模型拟合与预测

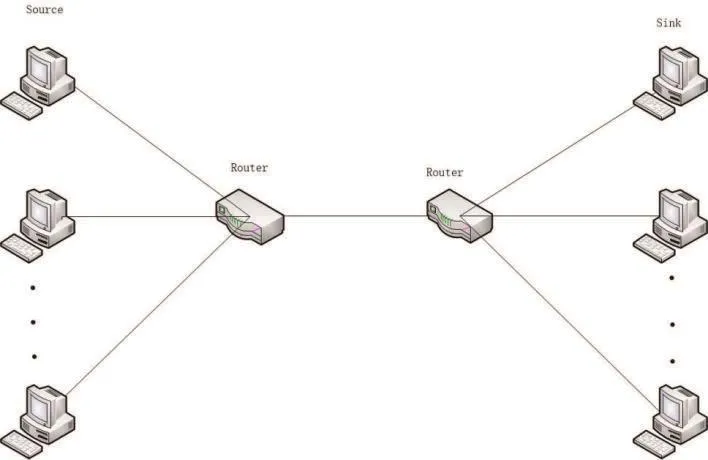
图4 仿真实验网络拓扑结构

时间序列模型拟合与预测结果如图3所示。从中可以看出，时间序列模型可以较好的模拟网络流量的特性，预测的数据基本在可信区间内。

四、基于NS2的随机早期检测算法模型实现

本文使用NS2对网络模型进行仿真实验，NS2是一种面向对象的网络仿真器。在模拟实验中，模拟了多个用户以在一定范围内将数据包随机发送到路由器，并在路由器上设置了路由节点以处理数据包的传输带宽。通过拥塞控制算法对队列进行拥塞管理，故本文以拥塞队列的长度作为算法优劣的评价指标。

本次仿真实验所使用的网络拓扑结构见图4。

4.1 RED算法的仿真实现

在网络的传输过程中，当网络中传输分组的数目所需资源大于由于路由节点的存储资时，队列的累积便会造成网络拥塞。而路由器处的队列长度则能很好的反应网络拥塞情况以及拥塞管理情况。

表3 实验仿真数据表

首先对RED算法进行仿真实验，所选取的实验仿真数据见表3。

RED算法伪码在前文中已经提到，本文在将其改进后应用到NS2软件中，在仿真数据下的平均队列长度如图5中RED曲线所示。当平均队列长度小于最小阈值长度时，路由节点的状态正常，数据包根据调度算法进行排队。当平均队列长度在最小阈值和最大阈值之间时，路由节点将以一定概率p丢弃数据包；当平均队列长度超过最大阈值时，路由节点将丢弃所有流量数据包。可以看出，RED算法在一定条件下可以缓解网络拥塞，但由于缺少预测网络流量这一步骤，导致多个拥塞和丢包事件。