一类忆阻神经元的电活动多模振荡及Hamilton 能量反馈控制1)

安新磊 张 莉

(兰州交通大学数理学院，兰州 730070)

(兰州理工大学电气工程与信息工程学院，兰州 730050)

(兰州工业学院基础学科部，兰州 730050)

引言

神经系统以神经元的不同放电活动对信息进行编码、传递和解码，由此实现神经系统信息的产生、整合和传输[1].神经元即神经细胞，是神经系统传输信息的最基本的元素，只有清晰地了解其各种环境下的放电模式，才能更好地理解神经网络以及各组织细胞的运行规律.各种神经元的建立在很大程度上有助于了解神经元的放电机理，Hodgkin 和Huxley 在1952 年 提 出 的Hodgkin-Huxley(HH)模型开创了神经元模型建立的新纪元，此后各种改进的数学模型如Morris-Lecar(ML)、FitzHugh-Nagumo(FHN)、HR 神经元系统相继建立.学者们可以从数学和物理的角度分析神经元的放电行为[2-6].

目前研究表明，外界电磁场对神经系统接收、处理和传递生理信息有着重要的影响[7-8],研究外界电磁场对生物神经元的作用机制已成为近年来备受关注的课题.马军教授在文献[9]中考虑到离子穿越细胞膜以及外界电磁辐射下，细胞内外的电生理环境会发生改变而产生电磁感应，进而会影响神经元的放电模式，首次提出用磁通来描述电磁场的作用，改进了一个四维HR 神经元模型，并进行了初步讨论.随后，其团队讨论了该模型的动力学性质[10-11]，通过改变初始状态可以观察到多种电活动模式，如静息态、峰放电态、簇放电态、混沌放电等，同时指出，该改进模型的网络也可用于研究大脑和中枢神经系统神经元的集体行为，并可以解释电磁辐射诱发疾病的潜在机制.

神经元模型在各种不同的放电活动中，加周期分岔是重要的分岔和神经放电节律转迁类型之一[12]，对其深入研究将为认识节律转迁的理论框架及理解神经编码的机制提供了一定的依据.因此运用非线性理论及其数值仿真探究电磁场下神经元膜电压的放电活动有着重要的实际意义[13-16].Chen 等[13]提出了一种具有线平衡点的三维耦合神经元磁控忆阻HNN 模型，研究了在双参数平面上Fold 和Hopf 分岔集和不同的稳定性区域，发现具有不同振幅吸引子共存现象.Bao 等[14]利用阈值磁控忆阻器产生的电磁感应电流代替二维(HR)神经元模型中的外电流，建立了具有全局隐藏模式振荡的三维HR神经元模型，并进行了相应的数值模拟，研究发现，该模型存在单稳态和双稳态的隐藏簇放电模式.混合模式振荡是一种复杂的振荡模式，是神经科学的一个研究热点[17-18].文献[17]介绍了神经元系统中混合模式振荡的研究情况和研究方法，并介绍了几种神经元模型中混合振荡模式的研究进展.文献[18]研究了在反馈参数和外界刺激电流变化下时具有磁流作用的Chay 神经元放电，并发现了丰富的复杂混合模式振荡.因此，对神经元系统多种模式放电行为的研究可以使我们进一步了解神经元的节律变化，本文借助双参数分岔对电磁感应下的HR神经元系统中的复杂加周期振荡和混合模式振荡进行深入研究.

神经元不同模式的放电状态离不开外界能量的触发，神经元信号的传输、转化和迁移需要能量消耗[19-22].持续的能量供应对维持系统的振荡是至关重要的，否则振荡行为将会减弱直至消失[19].磁通HR 神经元模型在各种外界刺激下具有不同的分岔模式及其能量特性，研究发现Hamilton 能量函数中的负反馈能有效地稳定混沌运动轨迹[20].此外，可以对具有不同吸引子的混沌系统进行哈密顿能量计算，并利用能量反馈有效控制系统中的混沌态[21].文献[23]中提出了一种Hamilton 能量反馈控制方法，可以在控制非线性系统到期望状态的同时，控测系统能量的转换和迁移.

基于上述讨论，本文主要从数学的角度对磁通HR 神经元模型的多模式放电行为进行全面分析，发现了磁通HR 神经元模型具有丰富的分岔结构并对其进行Hamilton 能量控制.通过数值仿真在双参数空间上的分岔结构，发现该系统存在含混沌的倍周期分岔、无混沌的加周期分岔、混合模式振荡以及共存模式振荡.其次，对磁通HR 神经元模型构建Hamilton 能量反馈控制器，研究结果发现该控制器可以有效地将混合模式振荡控制到多种周期的簇放电态.这些都是神经元异常放电研究领域的前沿课题，因此有必要对其进行深入研究.

1 模型描述及其分岔分析

根据电磁感应定理，引入磁通后的HR神经元模型如下(本文称为磁通HR 神经元系统)

正常情况下，系统(1)膜电压的放电活动会受到刺激电流I及其反馈增益k0变化的影响.本文基于Matcont 软件分析了随着参数I,k0同时变化时的Hopf 分岔点的分布，如图1(a)所示.由图可知，随着外界刺激电流I的变化，当0 ≤k0<=3.235 时，系统(1)存在3 个Hopf 分岔点.当k0=时，系统(1)存在两个Hopf 分岔点.当k0>时，系统(1)将出现一个Hopf 分岔点.不妨取k0=0.16,此时系统(1)的平衡点随外界刺激电流I的变化曲线如图1(b)所示，图中的蓝色曲线表示系统的平衡点，红色点Hi(i=1,2,3)表示Hopf 分岔点.通过数值计算得出在分岔点H1,H2,H3处的平衡点及其相应的特征根分别为

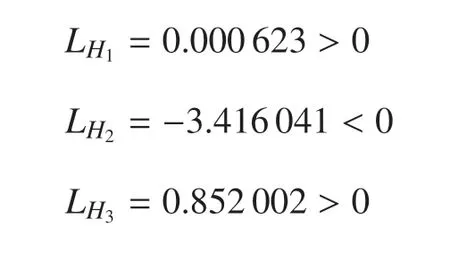
当第一Lyapunov 系数小于零时，其Hopf 分岔是超临界的；反之，Hopf 分岔是亚临界的.因此，系统(1)在分岔点H1,H3处发生亚临界Hopf 分岔，在分岔的H2处发生超临界Hopf 分岔.由于系统(1)的Hopf 分岔使其平衡点的稳定性发生了改变，并产生相应的极限环，因此有必要研究Hopf 分岔点附近膜电压的放电特征.

图1 系统(1)Hopf 分岔曲线、平衡点曲线和Hopf 分岔点Fig.1 The Hopf bifurcation curve,equilibrium curve and Hopf bifurcation points

2 双参数变化下伴有混沌的倍周期分岔模式

由于系统(1)在外界刺激发生改变时，很难保持系统参数固定不变，通常情况下系统(1)中的几个或者多个参数同时在特定范围内发生变化.因此，研究双参数平面上膜电压的放电活动将更具有现实意义.在本节中，主要分析了双参数平面上系统(1)的膜电压分岔行为，根据不同的双参数组合，系统(1)在两个参数空间中的分岔图如图2 所示，图中用不同的颜色绘制膜电压的不同的放电状态，并且图中右侧颜色栏用相应的数字进行标记(如用0 表示静息态，数值1 表示尖峰放电，数值2 表示周期2 簇放电态，白色区域表示周期大于等于20 簇放电或者混沌放电态).

图2(a)～图2(e)显示的是伴有混沌窗口的倍周期分岔模式.当以d和I作为参数变量时，在d[4.4,5.8],I[2.6,4]的参数平面上，相应的周期分岔图如图2(a)所示，系统(1)呈现出丰富而复杂的放电特性.沿着图2(a)中黑线从左下到右上的方向，膜电压x的倍周期分岔模式为：从周期1 的尖峰放电由倍周期分岔通向混沌态从周期3 簇放电由倍周期分岔通向混沌态从周期4 簇放电由倍周期分岔通向混沌态从周期19 簇放电由倍周期分岔通向混沌态.此外，从图2(a)中不难看出，在上述分岔模式过程中，随着周期数的增加，相应的周期的颜色带的宽度而逐渐变窄，并且相应的混沌窗口宽度也逐渐变小.图2(b)～图2(e)所示的参数平面上也具有类似分岔结构，都存在“梳子状”的混沌区域，并且有规律地分布着“舌形”周期窗口，这些周期窗口通过倍周期分岔结构与混沌区域相连接.在图2(f)和图2(g)中，分岔结构比较复杂，即都存在一个半环形的混沌区域，并且包括着半圆形的周期5 簇放电区域，其外围有规律地分布着“舌形”周期窗口，这些周期窗口也是通过倍周期分岔结构与混沌区域相连接.

图2 系统(1)关于x 的双参数分岔图Fig.2 Two-parameter bifurcation diagram of system(1)versus x

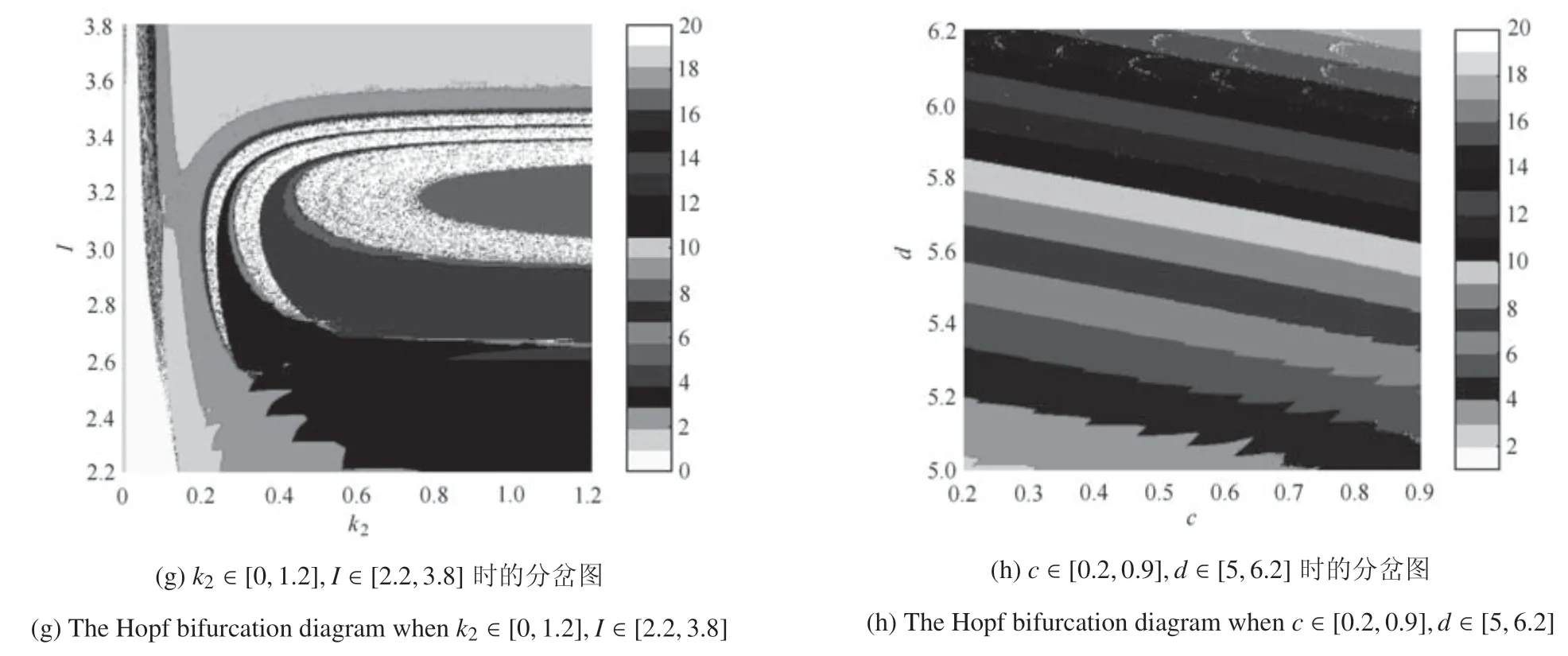
图2 系统(1)关于x 的双参数分岔图(续)Fig.2 Two-parameter bifurcation diagram of system(1)versus x(continued)

以参数d为变量时，当保持参数I=1.076 9d+2.138 4 不变，沿图2(a)中的黑线所示的方向，此时系统(1)膜电压峰峰间期(ISI)分岔图和变量x的分岔图如图3 所示.从图中可直观看出，随着参数d的增大，膜电压x放电模式为：尖峰放电态由倍周期分岔通向混沌周期3 簇放电态由倍周期分岔通向混沌周期4 簇放电态由倍周期分岔通向混沌放电态加周期簇放电态.系统(1)每经历一次混沌放电，放电的周期比混沌放电前的周期大1，并且随着周期的增大，相应的周期窗口及其混沌窗口逐渐变窄.从图3 中还可以观察到，当放电周期大于15 时，混沌窗口几乎消失，此时系统(1)的膜电压进入加周期分岔模式，图4 为图3 所对应的最大Lyapunov 指数图.

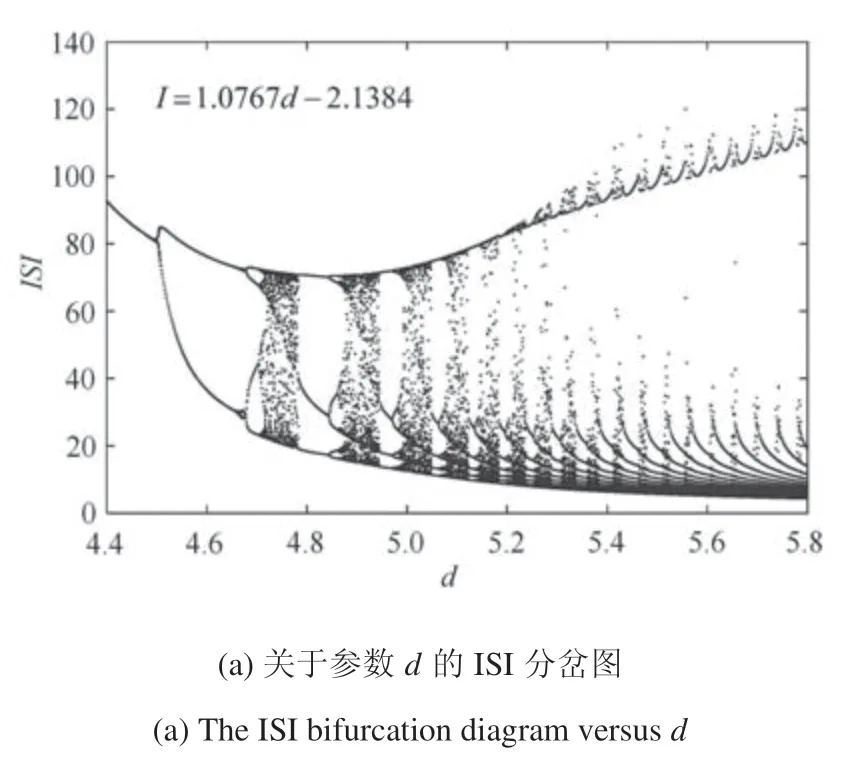
图3 系统(1)关于参数d 的分岔图Fig.3 Bifurcation diagram of system(1)versus parameter d

图4 对应于图3 的最大Lyapunov 指数图Fig.4 The maximum Lyapunov exponent graph corresponds to Fig.3

3 混合模式振荡及其共存模式震荡

3.1 混合模式振荡

混合模式振荡是非线性动力系统中特有的复杂模式振荡[26]，常常存在神经元系统中，即在一个周期振荡内，它是由一系列的大振幅振荡和小振幅振荡组成的，一般用符号Ls来描述这种振荡模式，其中L表示大振幅的数目，s表示小振幅的数目，而L0型的振荡模式表示没有小振幅振荡周期为L簇发电模式.

图5 显示了含有混合模式振荡的周期分岔图，与图2 中各图相比较，图5 出现了“周期层错位”特有的现象.在图5 所示的左侧区域，参数(k0,d)分别取值(0.627,4.939)和(0.738,5.276)时，系统(1)中膜电压分别处于周期3、周期5 簇放电态，其相应膜电压x时间响应分别如图6(a)和图6(c)所示.在图5 中“周期层错位”的右侧区域，当参数(k0,d)分别取值(0.641,4.962)和(0.756,5.271)时，系统(1)中膜电压x分别处于周期32和周期53的混合模式振荡放电态，其相应膜电压x时间响应分别如图6(b)和图6(d)所示.当保持参数d=3.5k0+2.5 不变，以参数k0为变量，沿图5 中白线所示的方向，系统(1)膜电压x的发放数(在一个周期内小振幅数占总振幅数的比例)随参数k0变化如图7 所示，由此可知，膜电压x的混合振荡模式变化为：.由于神经元相关的疾病通常都是神经元异常振荡模式放电引起的，这与本节研究的系统(1)存在混合模式振荡放电具有一定的相关性，因此控制系统(1)振荡模式放电到期望的放电状态具有重要的实际意义.

图5 k0[0,1],d [4.6,6]时系统(1)关于x 的双参数分岔图Fig.5 Two-parameter bifurcation diagram of system(1)versus x when k0 [0,1],d [4.6,6]

图6 系统(1)的时间响应图Fig.6 Time response diagram of system(1)

图7 膜电压的发放数关于参数k0 分岔图Fig.7 The spike count of membrane voltage versus parameter k0

3.2 共存混合模式振荡

通过数值模拟发现，这些“周期层错位”现象是由于系统(1)发生了混合模式振荡产生的，即在图5 中左侧区域为簇放电模式，右侧区域为混合振荡模式.此外，在这些“周期层错位”处，膜电压处于簇放电模式和混合模式振荡共存状态.

当参数(k0,d)取(0.699 4,5.133 0)时，系统(1)将出现初值为(0.1,0,0,0.1)时的周期4 和初值为(2,0,0,0.1)时的周期43混合模式振荡共存状态，其膜电压x的时间响应如图8(a)和图8(b)所示.当参数(k0,d)取(0.794 8,5.414 0)时，系统(1)将出现初值为(0.1,0,0,0.1)时的周期6 和初值为(2,0,0,0.1)时的周期63的混合模式振荡共存状态，其膜电压x的时间响应如图8(c)和图8(d)所示.当参数(k0,d)取两种不同的值时，系统(1)的两种初值在x−和y−平面上的吸引域如图9 所示.

4 基于Hamilton 能量的反馈控制

神经元系统中膜电压的不同放电模式、膜电位的迁移和转换都需要能量来维持，持续的能量供应对神经元系统的放电是至关重要的，否则振荡行为将会减弱或者消失.对于任意自治的动力系统

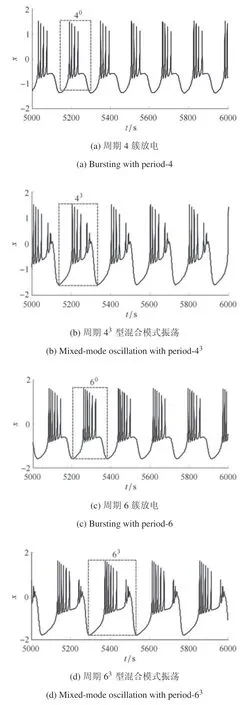
图8 系统(1)的时间响应图Fig.8 Time response diagram of the system(1)

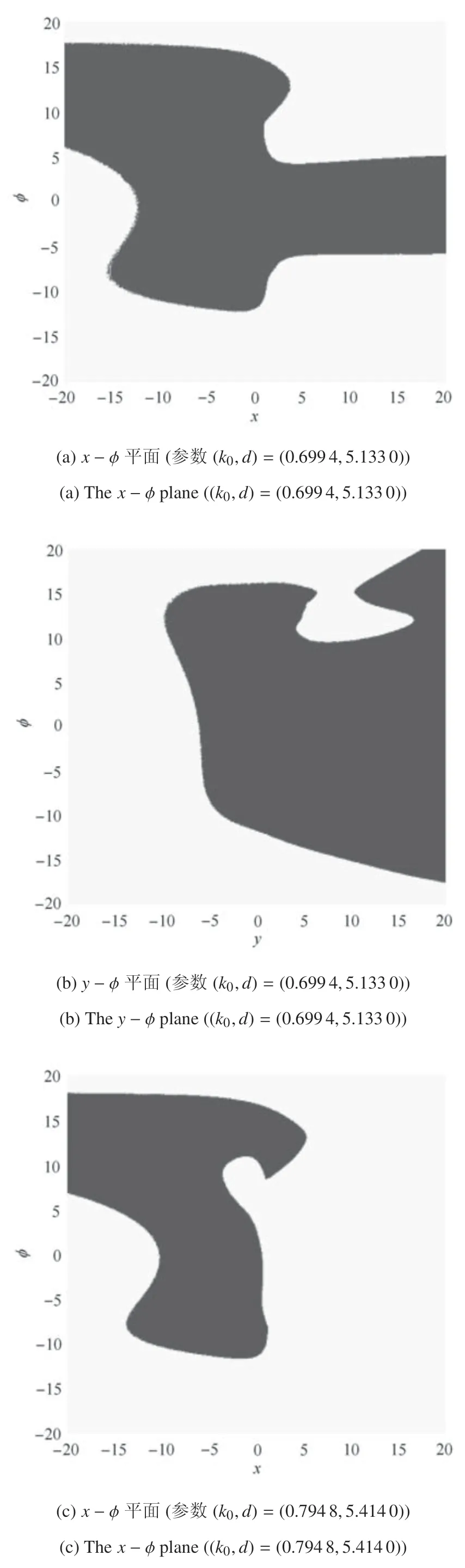
图9 系统(1)在不同初值时的吸引域Fig.9 The attractive basins of system(1)under different initial values

王春妮等[21]基于亥姆霍兹理论论证了一般广义动力学系统的哈密顿能量计算方法，对无量纲动力学系统以及非线性振荡电路的Hamilton 能量函数的计算进行了详细介绍.基于亥姆霍兹理论可知，向量函数f(X)可分解为

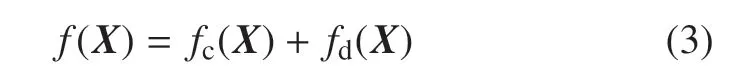
式(3)可以利用狄拉克-δ 和矢量的运算规则来证明，其中fc(X)表示漩涡场，它与系统的Hamilton 能量函数H的关系满足：=0.而fd(X)表示梯度场，它可以对系统运行的相轨迹进行约束，并且满足Hamilton 能量导数

能量的改变来自源于力场的做功，能量函数H满足式(3)和式(4).由此对于系统(1)可表示为

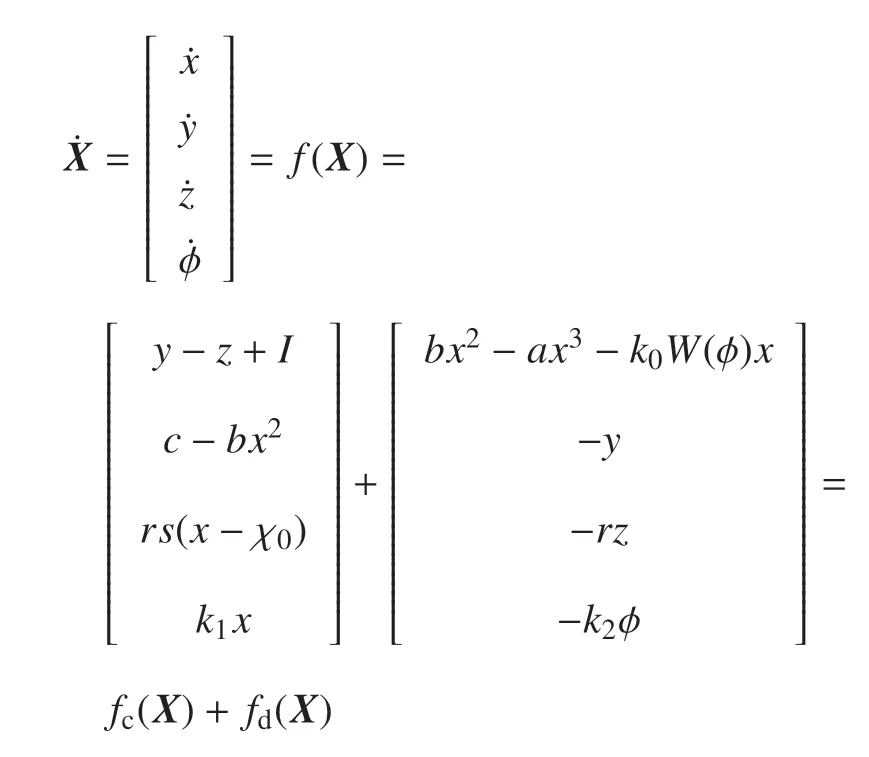
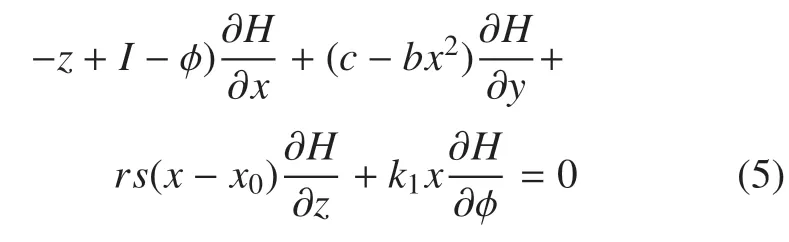
从物理角度看，在神经元电路中，电容器和感应线圈是主要的电子元件，电容可以存储电场能量(1/2CV2)，感应线圈可以存储磁场能量(1/2LI2)，这些物理场能量(H=1/2CV2+1/2LI2)经过标度变换后就是无量纲的Hamilton 能量.通过式(5)计算可得系统(1)的Hamilton 能量为

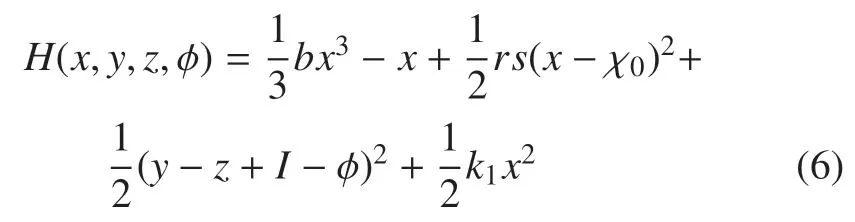
由此可知，式(6)正是所求的Hamilton 能量函数.本文作者在文献[23]中提出了一种基于Hamilton 能量的反馈控制方法，即将控制输入项kH作用到受控系统的某一项上去调控系统的群体变量.为了得到更丰富的振荡模式，这里将kH作用到系统(1)的第二项，受控下的磁通神经元系统如下

式中，k表示Hamilton 能量H的反馈增益，用于控制能量流的反馈强度，一般在[−1,1]内取值.当系统参数固定时，系统的能量靠反馈增益k来改变，即利用控制输入项kH来调制系统的动力学.受控系统(7)中的Hamilton 能量调制器为

下面讨论系统(1)的膜电压受Hamilton 能量控制后的放电行为.图10 为反馈增益k和外界刺激电流I的双参分岔图，从图中可以直观地看到反馈增益k能有效地控制系统(1)到不同的簇放电状态.

图10 k 2[0,0.3],I 2[2,3]时系统(1)关于x 的双参数分岔图Fig.10 Two-parameter bifurcation diagram of system(1)versus x when k [0,0.3],I [2,3]

当I=3 时，关于反馈增益k的ISI 分岔和在膜电压平面上的分岔如图11(a)和图11(b)所示.明显地，系统(1)的膜电压在原始的周期4 簇放电状态可以被Hamilton 能量控制器控制到典型的周期簇放电状态.图12 和图13 为加周期的簇放电状态，当取不同的反馈增益时，其周期放电模式为：.

簇放电是神经元系统中非常重要的放电模式，它能强化神经元之间的信息传输.另外，从图11 中也可以看出，磁通神经元系统(1)存在不规则的放电行为，其时间响应如图14 所示.当能量反馈增益分别取k=0.075 和k=0.083 时，磁通神经元系统(1)均展现了如下的不规则混合振荡模式

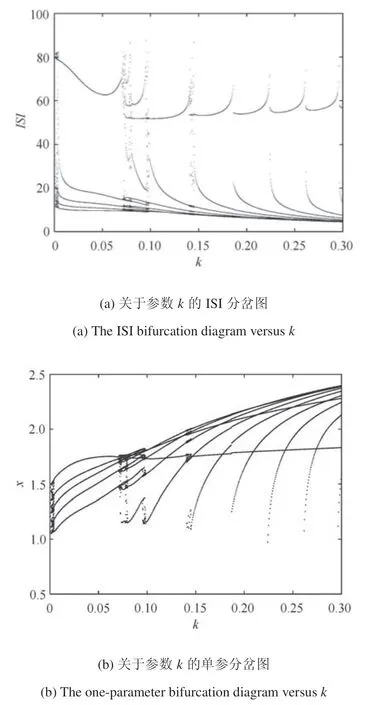
图11 系统(1)关于反馈增益k 的ISI 分岔和单参分岔Fig.11 The ISI bifurcation and one-parameter bifurcation of system(7)versus feedback gain k

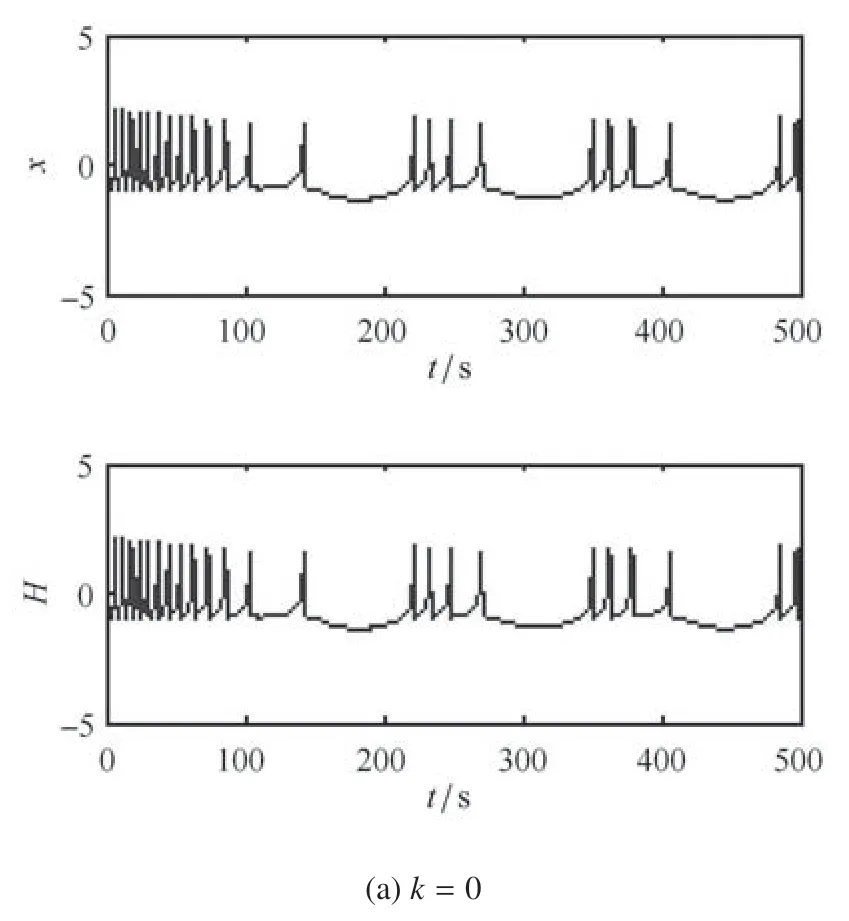
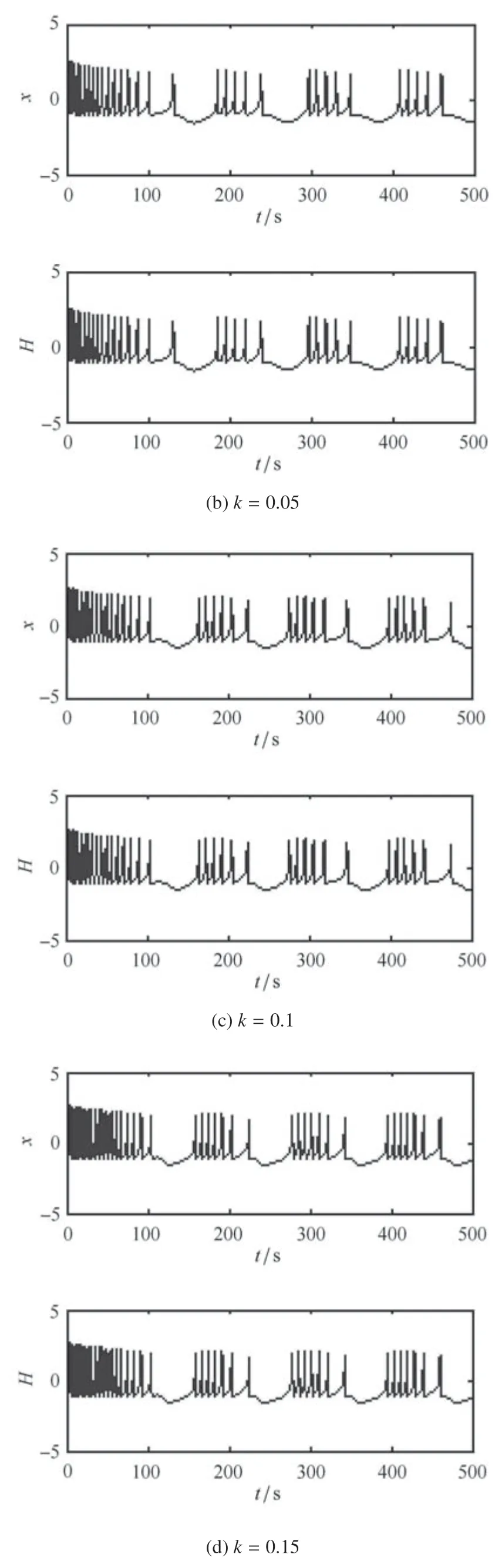
图12 周期簇放电和相应的Hamilton 能量曲线Fig.12 The period bursting states and corresponding Hamilton energy curves

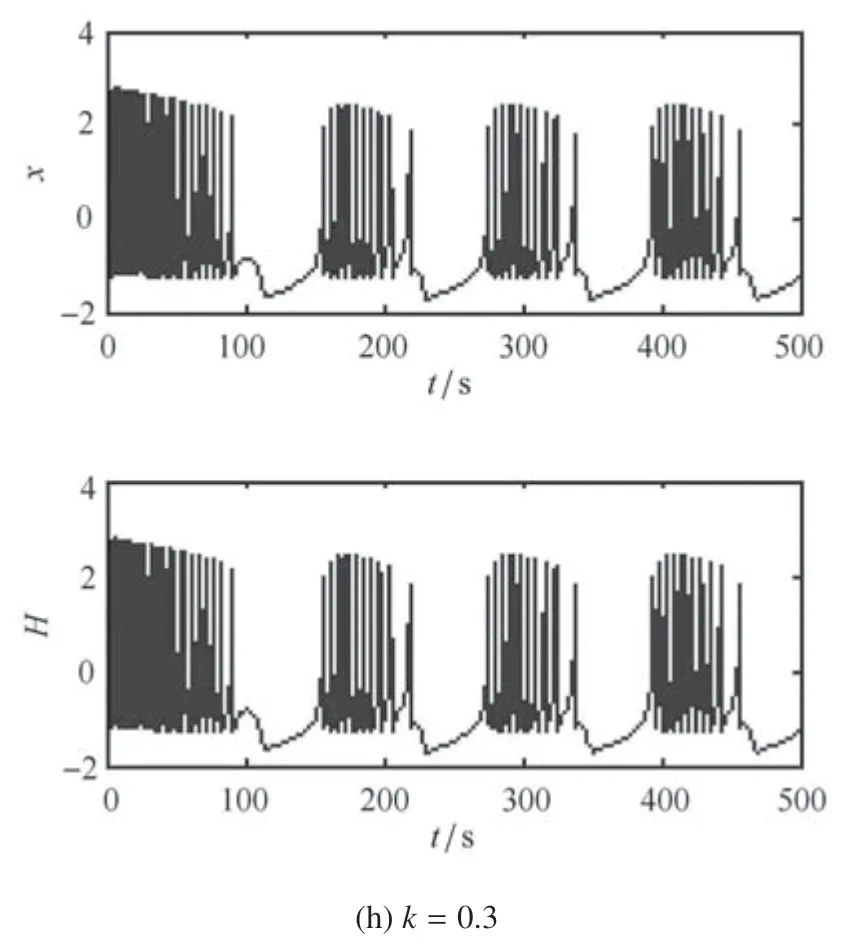
图12 周期簇放电和相应的Hamilton 能量曲线(续)Fig.12 The period bursting states and corresponding Hamilton energy curves(continued)

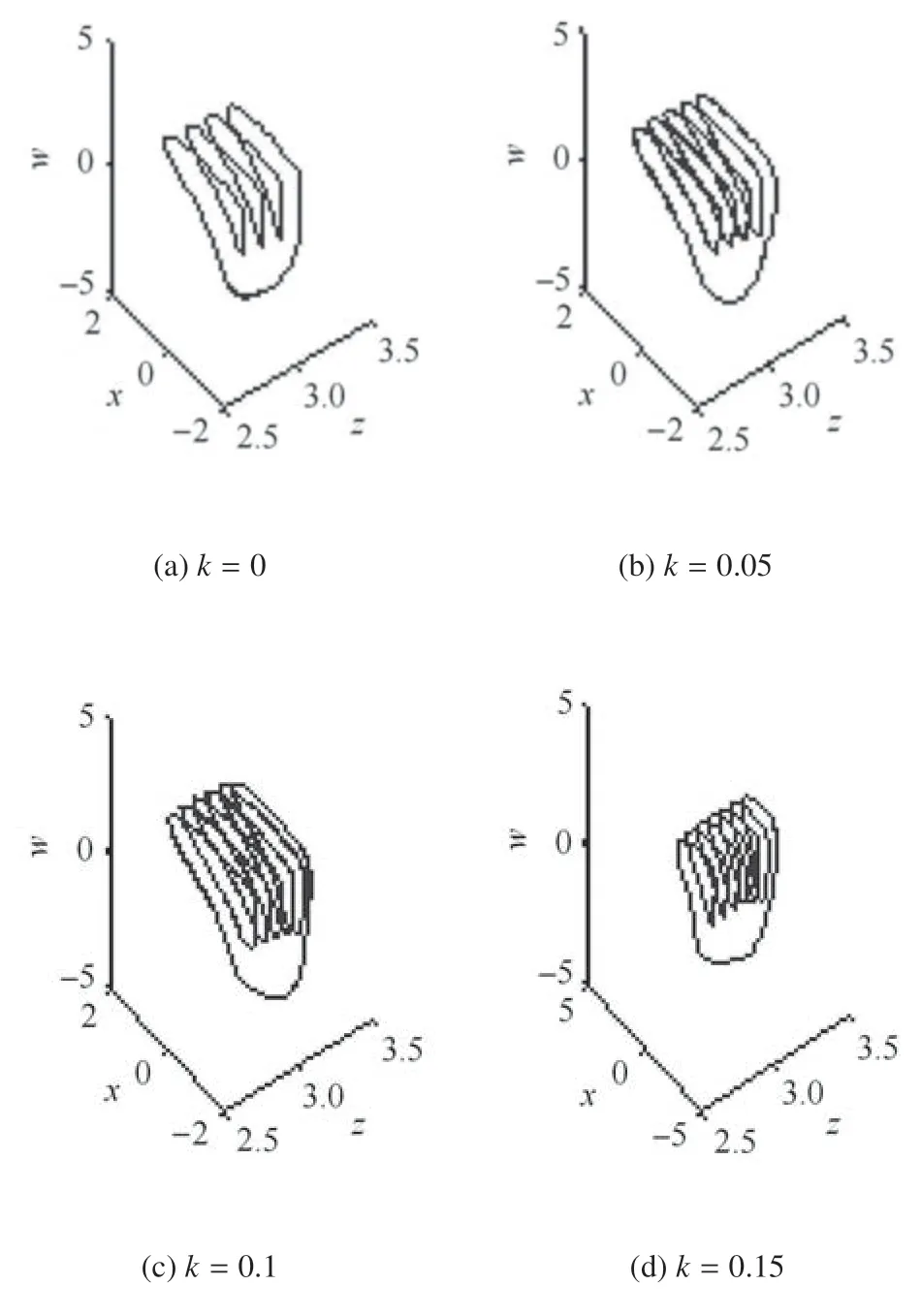
图13 在z −x −w 平面上的3 维相轨迹Fig.13 The 3-dimensional phase diagrams in z −x −w plane

图13 在z −x −w 平面上的3 维相轨迹(续)Fig.13 The 3-dimensional phase diagrams in z−x−w plane(continued)

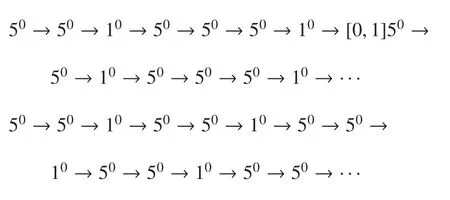
通过以上讨论可知，Hamilton 能量控制器可以有效地将磁通神经元系统控制到周期簇放电以及不规则的簇放电状态.同时，也可以从图12 中观察到膜电压簇放电时的能量迁移.

从式(6)可以看出，Hamilton 能量受到系统参数和初值的制约，同时又是基于无量纲的系统变量得到的，Hamilton 能量反馈从动力学角度来看是对相空间进行压缩或者放大，从而达到对系统所有变量群体调控的目的，最终达到对系统动力学的控制.从图14 可以看出，周期5 簇放电要比峰放电耗能多，大幅值峰放电要比小幅值峰放电耗能多.同时，可以设计合适的控制器，以期用最小的代价达到控制目的.

图14 复杂混合模式簇放电和相应的Hamilton 能量曲线Fig.14 The complexmixed-mode bursting states and corresponding Hamiltonian energy curves

能量反馈控制是通过反馈增益调节能量控制输入的强度而去调制神经元系统的膜电压振荡，进而动力学行为可以被调节.本文中，当反馈增益k取不同的值时，系统(1)能被很好地控制到不同的周期簇振荡状态.同时，我们也能清楚地看到膜电压在簇振荡和静息状态时Hamilton 能量的波动过程.这是因为神经元数学模型中的Hamilton 能量的变化趋势取决于模型中振荡模态的转变和外加电流，但主要依赖于振荡模态的变化.同时，由于神经元可以自行编码能量，Hamilton 能量的变化会稍滞后于电活动的变化[28].从图12 和图14 中可以看到，改进的HR 系统的Hamilton 能量函数曲线有正有负，正的Hamilton 能量为膜电压振荡提供能量，负的Hamilton 能量暂时不会被消耗，而是为后续膜电压振荡的能量储备被储存下来.这是由于神经元不仅是个耗能元件也是一个储能元件，从一个动作电位来看，神经元的能量由两部分组成，一部分是从血流中获得氧合的血红蛋白，表现为负的能量，用于能量的储存.一部分将脱氧的血红蛋白释放到血流中，表现为正的能量，用于能量的消耗[29-30].另外，在两个簇振荡之间的静息状态下，能量通常接近于0，但仍然有较低水平的振荡，故仍有少量能量释放，直到下一个簇振荡或峰振荡开始.

对无量纲后的神经元系统来说，膜电压的振荡都需要一定的能量，因此Hamilton 能量的吸收和释放与膜电压紧密相关.对Hamilton 能量的研究为理解神经元电活动的信息编码和能量迁移提供了思路，也对分析振动模态转换过程中能量转移有一定的参考.

5 结论

本文通过研究磁通HR 神经元系统在双参数空间上的分岔结构，发现该系统存在丰富的分岔结构，即含混沌的倍周期分岔、无混沌的加周期分岔及其混合模式振荡.为了控制磁通HR 神经元系统的放电模式，本文通过建立Hamilton 能量反馈控制器，可以有效地将磁通HR 神经元系统中的膜电压控制到不同周期的簇放电状态，同时，在控制过程中，可以探测到膜电压簇放电时能量的变化状态.上述的研究为进一步探索磁通神经元的分岔模式和了解电磁场下神经元的能量控制提供了有益的探讨.