非保守非线性刚−弹−液−控耦合分析动力学及其应用研究1)
2020-08-11李海波刘世兴宋海燕梁立孚
李海波 刘世兴 宋海燕 梁立孚
(北京强度环境研究所可靠性与环境工程技术重点实验室,北京 100076)
(辽宁大学物理学院,沈阳 110036)
(哈尔滨工程大学力学一级学科博士点,哈尔滨 150001)
引言
非保守非线性刚−弹−液−控耦合分析动力学是与航天动力学和多体动力学相关的重要研究课题之一.对于这一学术领域在国内外的研究进展,文献[1-2] 做了很好的综述.文献[3-12] 可以反映出近年来新的进展.此外,还参考了充液系统动力学[13]、分析动力学[14-15]、工程控制论 [16] 和自动控制 [17-19]的几部专著.对于20 世纪的研究情况,文献[20] 指出:“由于多柔体构形的复杂性,目前解决多柔体动力学问题主要是依赖于数值的、定量的分析方法,几乎没有人进行解析的分析讨论,这对于深刻把握系统的非线性力学实质、预测系统的全局动力学现象是十分不利的.因此,极有必要开展多柔体系统的理论分析,当然,这是一个十分复杂的问题,解决它可能需要很长的时间.” 作者有关的研究工作就是在这一论述的启发下展开的.由于分析力学的特点,应用分析力学中的Hamilton 型变分原理和Lagrange 方程进行多柔体系统的解析的分析讨论和理论分析是一条可行的途径.经过十余年的潜心研究[21-31],至2013 年研究非线性、非保守柔体动力学拟变分原理及其在航天器动力学中的应用[32],多柔体系统的解析分析讨论和理论分析已经基本实现.进而,适时地拓宽了研究领域:应用现代非线性力学的理论成果和分析方法对航天工程中的刚(柔)−液−控耦合动力学的耦合机理进行深入探索,并预见带柔性附件充液航天器的动力学响应特征,从而为复杂结构航天器的设计与分析提供理论参考[2].又经过多年的艰苦的研究工作[33-41],至2019 年《力学进展》发表了《连续介质分析动力学及其应用》一文,比较全面地介绍了研究成果[42].正是在经过新世纪以来的近20 年的研究积累的基础上,尝试性地研究了非保守非线性刚−弹−液−控耦合系统的Hamilton 型拟变分原理,从系统的Hamilton 型拟变分原理出发,借助Lagrange-Hamilton 体系,建立了刚−弹−液−控耦合系统的Lagrange 方程,应用该Lagrange 方程建立了系统的控制方程.并应用Lagrange 方程建立了相应的有限元计算模型,研究了系统的控制方程的应用,探索进行解析的分析讨论的途径.
本文研究了航天器在大气层中飞行的情况,航天器在大气层外飞行的情况将在后续的工作中讨论.
1 非保守非线性刚−弹−液−控耦合系统的Hamilton 型拟变分原理
非保守非线性两类变量刚−弹−液−控耦合分析动力学的Hamilton 型拟变分原理为
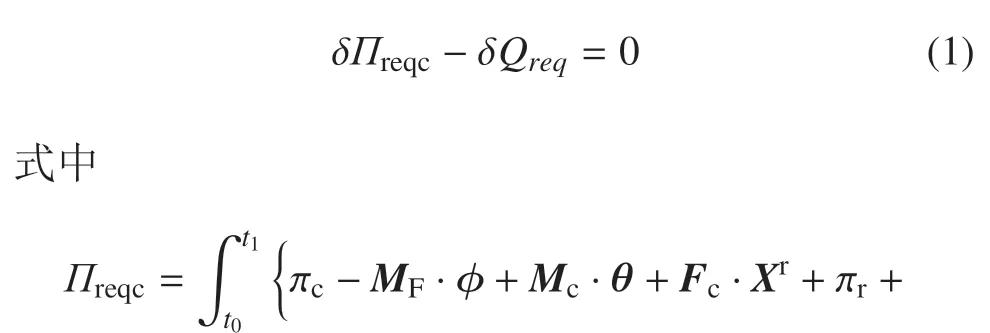
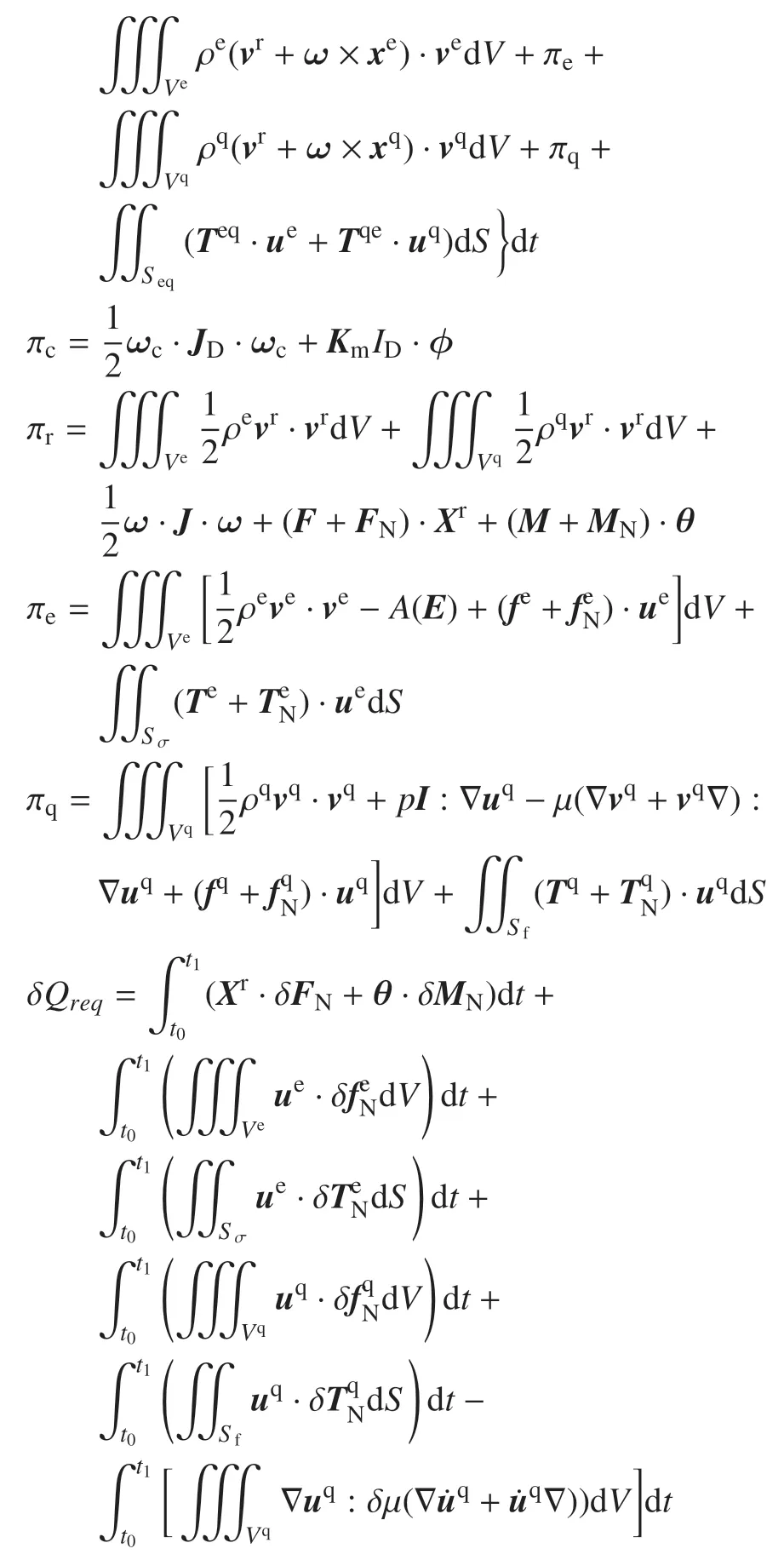
此项为刚−弹−液−控耦合系统的余虚功表达式.
先决条件为

式中,Xr为系统质心的矢径,x为系统中任意一点到质心的矢径,θ为系统刚化后的转角,J为系统刚化后的转动惯量(假设J为常量),F为保守力主矢,FN为非保守力主矢,M为保守力主矩,MN为非保守力主矩,ρq为流体质量密度,ρe为弹性体质量密度,fe为弹性体的保守体积力,为弹性体的非保守体积力,fq为流体的保守体积力,为流体的非保守体积力,µ为黏性系数,I为单位张量,p为压强,Te为弹性体的保守面积力,为弹性体的非保守面积力,vr为刚体平动的速度,ve为弹性体质点的速度,ue为弹性体质点的位移,Tq为流体的保守面积力,为流体的非保守面积力,vq为流体质点的速度,uq为流体质点的位移,∇为梯度算子,Vr为刚体体积,Vq流体体积,Sw为流体的位移边界面,Sf为流体的应力边界面,Su为弹性体的位移边界面,Sσ为弹性体的应力边界面,Seq为弹−液交界面,Tqe为Seq处的液体面积力,Teq为Seq处的弹性体面积力,Km为电动机转矩系数,JD为电动机转子转动惯量,MF为实现所需的舵面偏角导致的电动机负载转矩,ωc为电动机转子转动角速度,并且ωc=dϕ/dt,ϕ为电动机转子的转角,Mc为舵面偏转引起的力矩的增量,Fc为舵面偏转引起的力的增量.
注意到δΠreqc为刚−弹−液−控耦合动力学两类变量的拟变分原理的定积分形式泛函的变分;πc为Πreqc的一个组成部分(形式上与电动机动力学的Hamilton 变分原理的泛函相同,认为是保守系统);πr为Πreqc的一个组成部分(形式上与刚体动力学的Hamilton 型拟变分原理的泛函相同);πe为Πreqc的一个组成部分(形式上与弹性动力学的Hamilton 型拟变分原理的泛函相同);πq为Πreqc的另一个组成部分(形式上与流体力学的Hamilton 型拟变分原理的泛函相同).明显可见,刚−弹−液−控耦合系统两类变量的Hamilton 型拟变分原理的定积分形式泛函Πreqc不是电动机动力学的Hamilton 变分原理的泛函、刚体动力学的Hamilton 型拟变分原理的泛函、弹性动力学的Hamilton 型拟变分原理的泛函和流体动力学的Hamilton 型拟变分原理的泛函的组合,而是多出控−刚耦合项−MF·ϕ+Mc·θ+Fc·Xr、刚−弹耦合项、刚−液耦合项∫和弹−液耦合项.明显可见,刚−弹−液−控耦合中的刚−弹耦合和刚−液耦合是惯性耦合,而弹−液耦合和控−刚耦合是接触耦合.这里说明,对于弹−液耦合,在弹−液交界面Seq处,内力满足平衡关系[43-44]
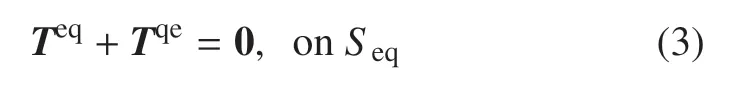
位移满足协调关系
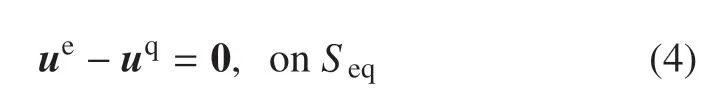
两类变量的刚−弹−液−控耦合系统的动能为
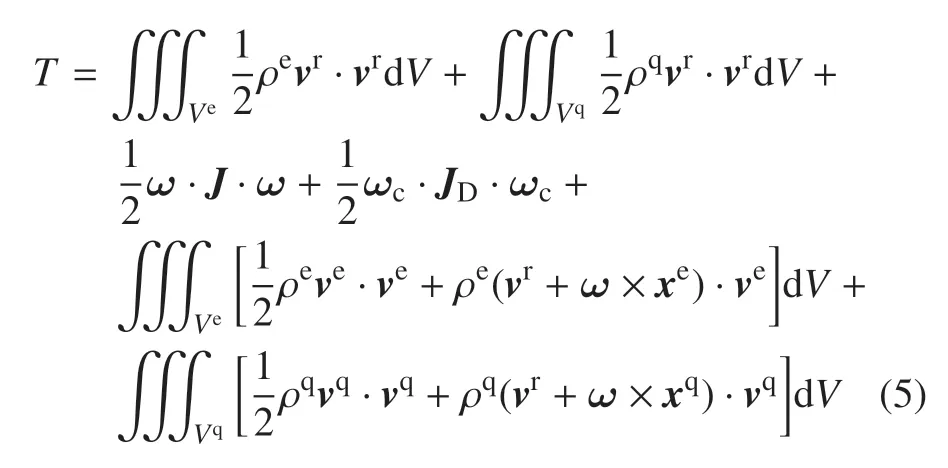
刚−弹−液−控耦合系统的势能为
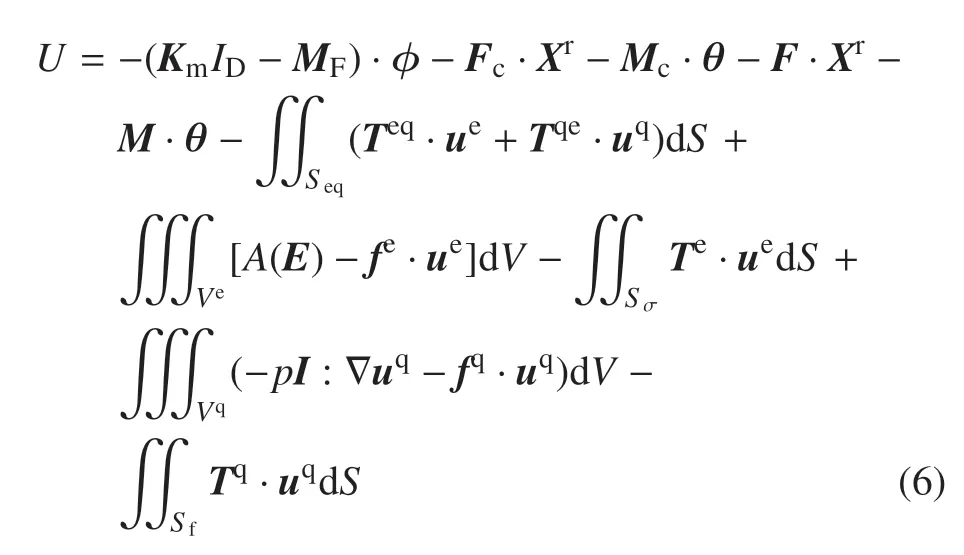
刚−弹−液−控耦合系统的拟势能为

2 刚−弹−液−控耦合系统的Lagrange 方程
根据式(5)~式(7),式(1)可改写为

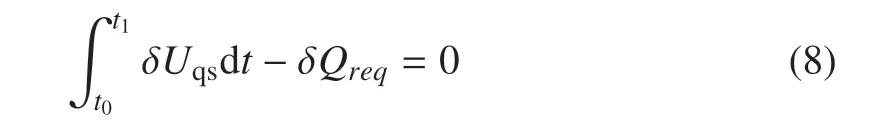
先决条件(2)的变分式为
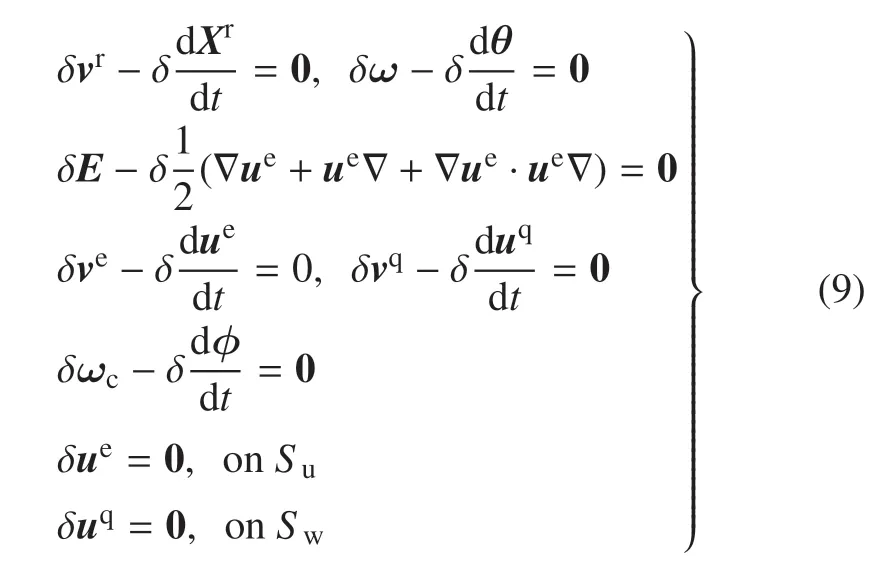
将先决条件的变分式(9)代入式(8),进行分步积分,可得
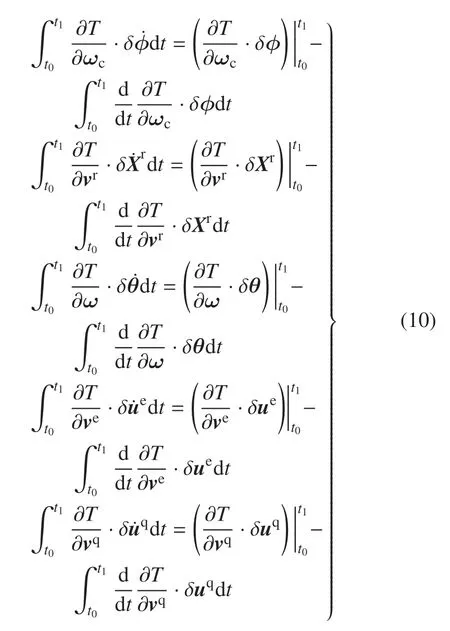
将式(10)代入式(8),在时域边界t=t0和t=t1处取δue=0,δuq=0,δXr=0,δθ=0,δϕ=0,则可得

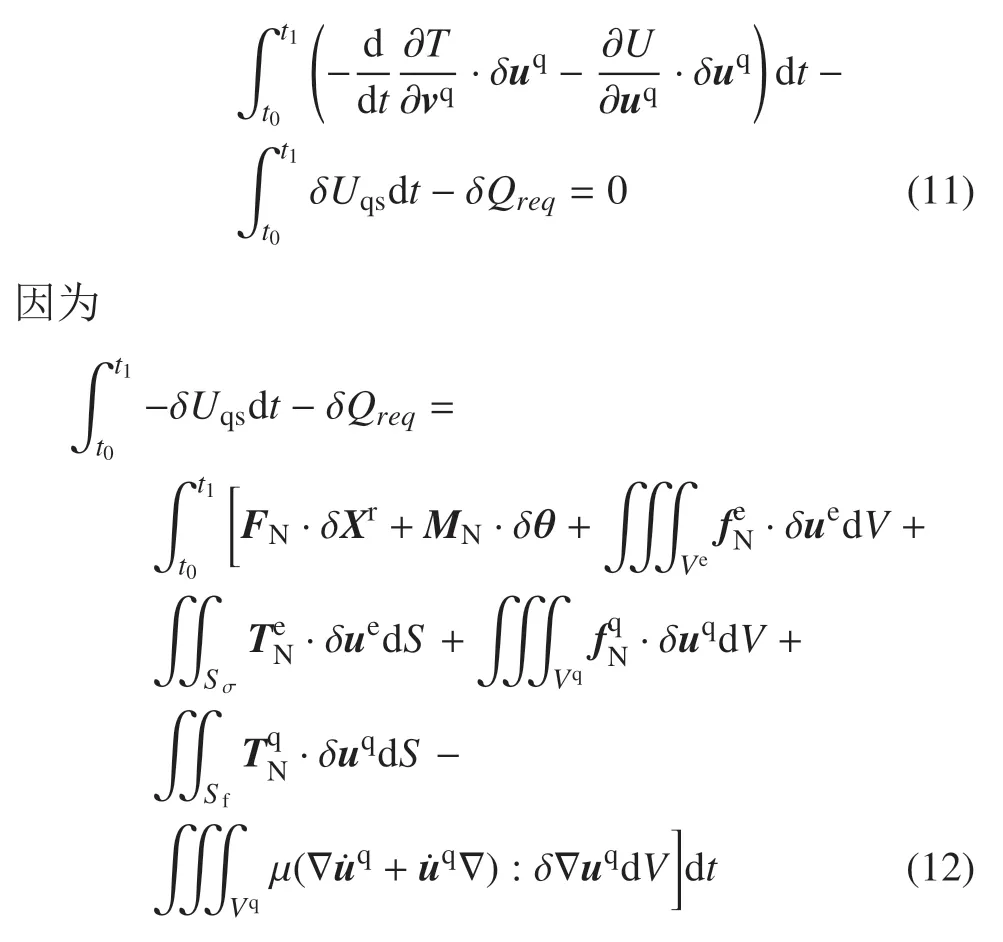
应用Green 定理,并考虑到先决条件(9)中的流体位移边界条件,可得

进而可得

由于δue,δuq,δXr,δθ,δϕ的任意性,故由上式可得两类变量的刚−弹−液−控耦合系统的Lagrange 方程组

3 应用Lagrange 方程建立刚−弹−液−控耦合系统的控制方程
应用刚−弹−液−控耦合系统Lagrange 方程推导其控制方程.为此,需要推导计算Lagrange 方程中的有关动能和有关势能的各项.首先,推导计算Lagrange 方程中的有关动能的各项

然后,推导计算Lagrange 方程中的有关势能的各项为

应用Green 定理,并考虑到先决条件(9)中的弹性位移边界条件,可得

将上式代入式(17)的第四式,可得

应用Green 定理,并考虑到边界条件(9)中的流体位移边界条件,可得

将式(16)~式(20)代入Lagrange 方程(15)中,可得

应用可变函数选值的理论,进而推导出两类变量的非保守非线性刚−弹−液−控耦合动力学的控制方程


比较式(31)和式(34),可得

建议注意:在无际边界面Seq处
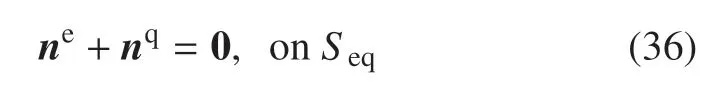
两类变量的非保守非线性刚−弹−液−控耦合分析动力学的控制方程(26)~(34)改写为

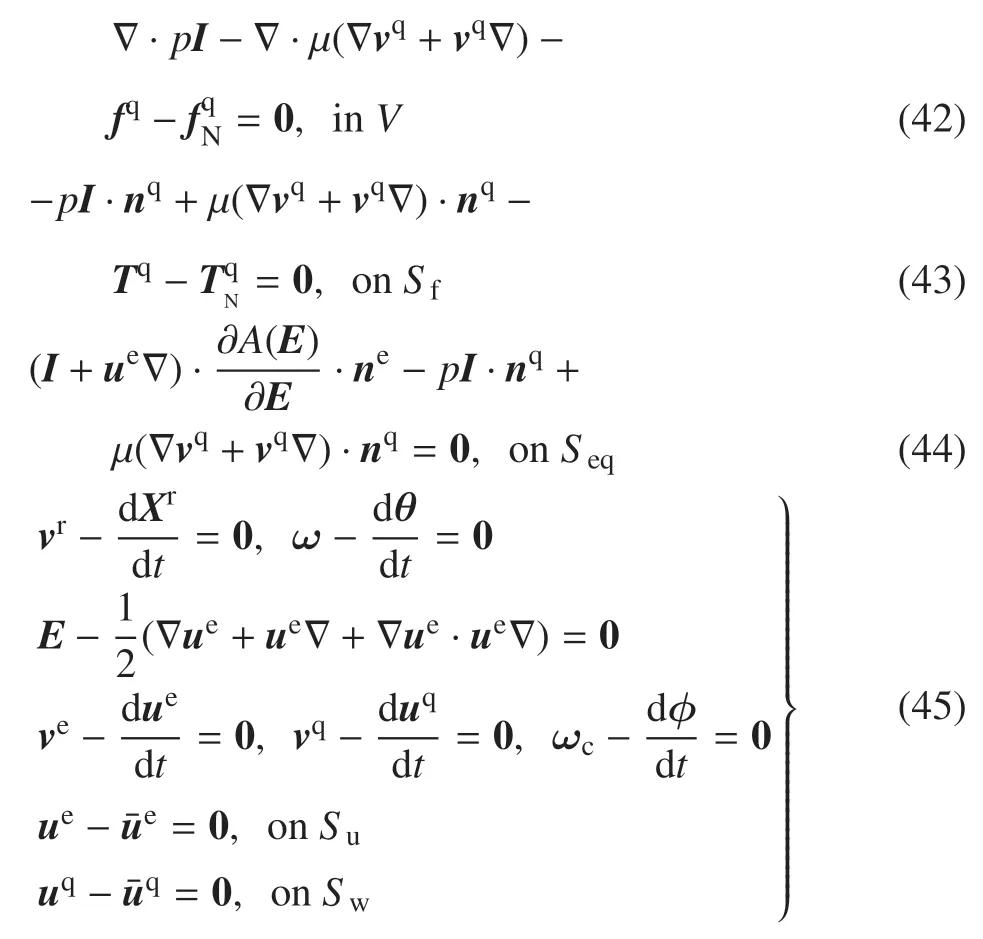
还有一个重要的先决条件:在无际边界面Seq处

退化到一类变量的非保守非线性刚−弹−液−控耦合分析动力学问题,则其控制方程为


这里借助非保守非线性刚−弹−液−控耦合分析动力学的控制方程(47)~(56)来说明刚−弹−液−控耦合的耦合机理.
弹−液交界面处力的平衡方程(54)和位移协调方程(55)说明弹−液耦合是接触耦合.
刚体动力学的轨迹方程式(48)中的Fc项和控制动力学的方程式(47)中的MF项说明控−刚耦合是接触耦合.同样,刚体动力学的姿态方程式(49)中的Mc项和控制动力学的方程(47)中的MF项也说明控−刚耦合是接触耦合.
这里存在一个问题,即似乎看不出控制对弹和液的影响.其实不然,控制是通过方程(48)和(49)影响刚体的Xr和θ,进而影响弹和液的.反之,弹和液是通过方程(48)和(49)中的惯性耦合项影响刚体的Xr和θ,而控制中的ϕ是按照对航天器Xr和θ变化规律的要求设计的.
4 刚−弹−液−控耦合系统Lagrange 方程的应用研究
4.1 应用非保守非线性刚−弹−液−控耦合系统Lagrange 方程建立位移协调元模型
这里说明,为了书写简捷紧凑,前面的理论推导部分采用实体张量符号;为了编写计算程序的方便,后面的有限元法研究,采用指标张量符号书写.将弹性连续体划分为n个单元,取为自变函数,将液体连续体划分为m个单元,取为自变函数,它们满足如下条件:

这里说明,由于弹−液耦合产生在弹−液交界面处,为了方便起见,在划分有限元法的元素的时候,总是希望把弹−液交界面处理为有限元法中的无际边界面.这就是条件(6)的来源.弹性体单元、液体单元和弹−液交界面处单元如图1 所示.

图1 刚−弹−液−控耦合体的有限元素和界面关系Fig.1 The relationship between the element and the interface in finite element method of rigid-elastic-liquid-control coupiing

图1 刚−弹−液−控耦合体的有限元素和界面关系(续)Fig.1 The relationship between the element and the interface in finite element method of rigid-elastic-liquid-control coupiing(continued)
刚−弹−液−控耦合系统Lagrange 方程表示为

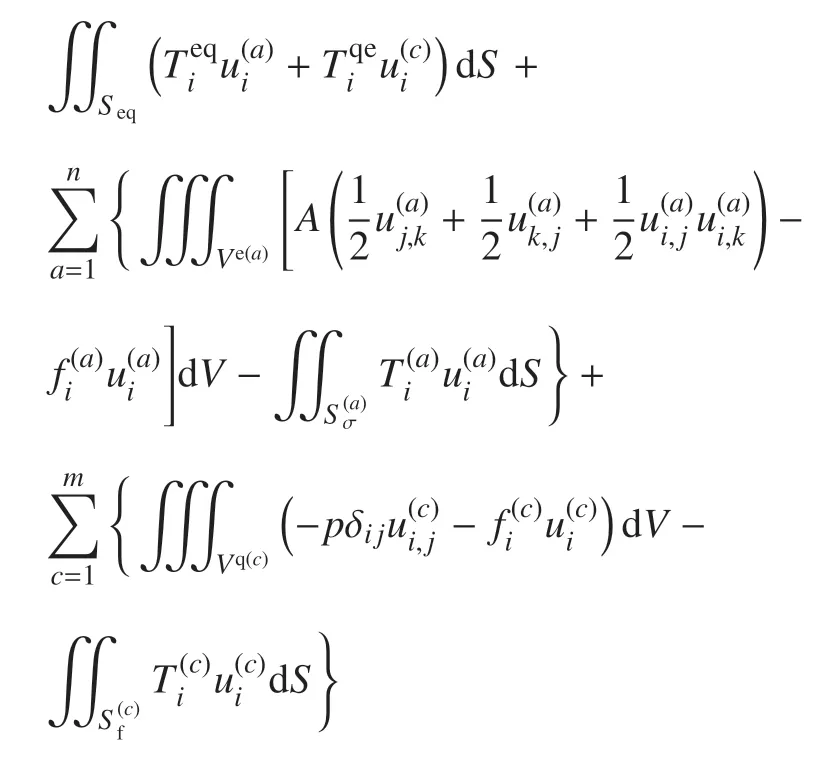
其先决条件为

这便是适于有限元计算的非保守非线性刚−弹−液−控耦合系统的Lagrange 方程,它提供了有限元计算的位移协调元模型.
4.2 应用非保守非线性刚−弹−液−控耦合系统Lagrange 方程建立位移杂交元模型
应用Lagrange 乘子法,将式(58)代入势能的表达式中,则有
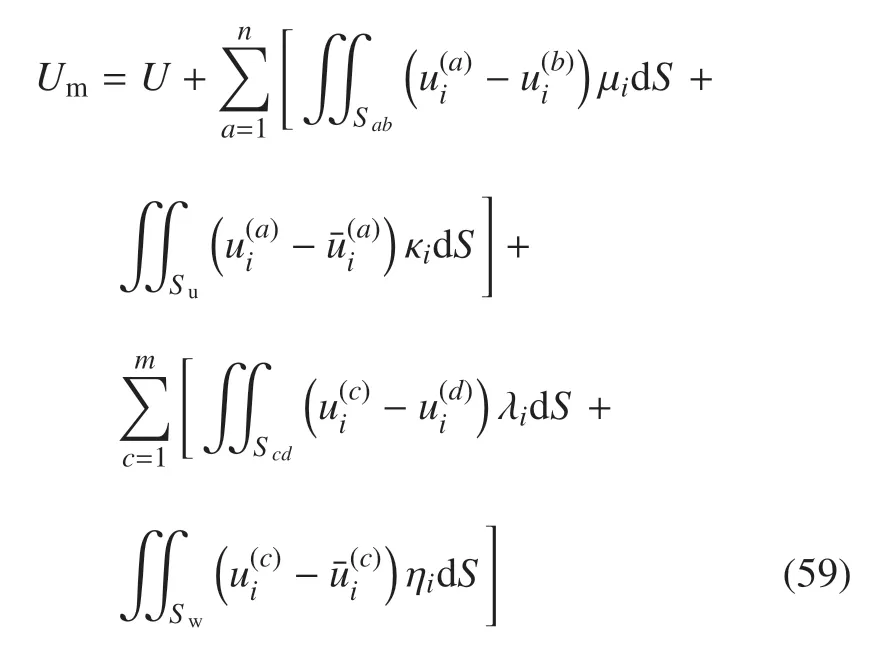
应用Lagrange 方程,则有

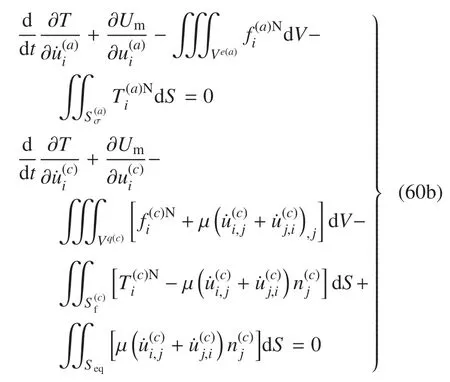
经过一系列的运算,解得Lagrange 乘子的表达式

将式(61)、式(63)、式(64)和式(66)代入式(59),经变换,可得适于有限元计算的位移杂交元模型.
通过如上的推导有限元列式的过程可以发现,应用Lagrange 方程推导的一个特点是不出现对时间的积分.从事飞行器强度计算的学者明白,强度计算是相对于特定的“设计情况”进行的,而所谓设计情况,是飞行器飞行中的某个部位受力严重的特定的瞬间状态,并不涉及对时间的积分.这也说明应用Lagrange 方程来解决这类问题的优越性.应用Lagrange 方程建立有限元模型的另一个优越性,不涉及对时间的积分特性便于将大量静力学有限元素法的计算技术和开发的大量计算程序移植到刚−弹耦合动力学、刚−黏弹耦合动力学、刚−液耦合动力学、刚−热−弹耦合动力学、刚−弹−液耦合动力学和刚−弹−液−控耦合动力学中.
4.3 非保守非线性刚−弹−控耦合分析动力学问题
在控制方程(47)~(56)中,如果忽略式(54)和式(55)的影响,可以将弹−液耦合解耦,从而可以独立的研究刚−弹−控和刚−液−控耦合的应用问题.
本节研究非保守非线性刚−弹−控耦合动力学问题,其控制方程为式(47)~式(51),但是,要忽略关于ρq的惯性耦合项.在考虑惯性耦合的情况下,研究梁式太阳能帆板的振动问题,其特性方程为

式中,N为离心惯性力.
与一般的特性方程相比,多出离心惯性力导致的“−N∂2w/∂x2”项,其角频率方程为
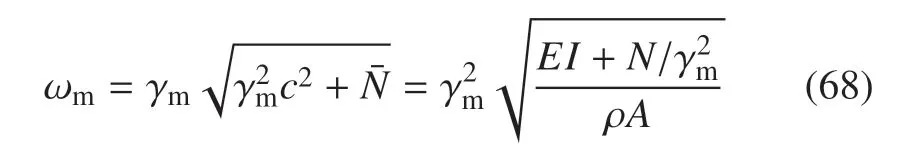
另一方面,同样在考虑惯性耦合的情况下,研究自由梁的振动问题(可以将飞行器简化为自由梁或者称为无约束梁),研究结果表明,无论是自由梁的奇数阶振型或者偶数阶振型,梁中的质点都不是绕梁的中性轴做往复振动,而是绕振动中心轴作往复振动.梁的中性轴和振动中心轴之间,既有往复运动的线位移D,又有往复摆动的角位移C

其奇数阶振型和偶数阶振型如图2 和图3 所示.
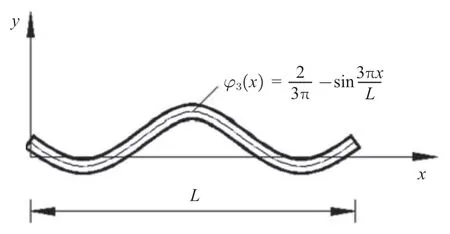
图2 无约束梁自由振动的三阶振型Fig.2 The third mode of free vibration of unconstrained beams

图3 无约束梁自由振动的二阶振型Fig.3 The second mode of free vibration of unconstrained beams
这便说明,如果简化为自由梁的飞行器被激振前为水平等速直线运动,则自由梁振动的奇数阶振型和偶数阶振型的作用,可以使自由梁的运动轨迹和运动姿态产生微小的扰动.进一步引申这一结果的意义,因为飞行器的刚体运动与控制之间存在接触耦合,振动对刚体运动(运动轨迹和运动姿态)的影响可以耦合到控制系统中去.这就为研究飞行器结构振动对控制的影响提供了参考.
4.4 非保守非线性刚−液−控耦合分析动力学问题
本节研究非保守非线性刚−液−控耦合动力学问题,其控制方程为式(47)~式(49)、式(52)、式(53),但是,要忽略关于ρe的惯性耦合项.
参照刚−弹−控耦合动力学的研究情况,研究刚−液−控耦合动力学也分两个方面.一方面刚体动力学产生的惯性力对流体动力学的影响.另一方面,研究流体动力学产生的惯性力对刚体动力学的影响,进而研究其对控制系统的影响.太空的环境条件是十分严酷的,特别是轨道空间存在高真空、高辐射和失重状态的影响.在失重状态下,表面张力的作用凸显出来,因此,应着重研究在失重条件下的表面张力的特性.这一研究与文献[45]的论述是一致的:在涉及液体的相关耦合问题方面,自由液面边界问题比较复杂,可分为运动学边界条件和动力学边界条件,需要对于线性和非线性情形(特别是航天背景中表面张力需要考虑表面张力、接触角及接触线动力学问题边界条件)分别展开讨论.
4.5 非保守非线性弹−液耦合分析动力学问题
姿态方程、轨迹方程和控制系统方程一起,可以组成飞行器的有控飞行力学问题.如果假设这类有控飞行力学问题已经解决,则可近似地认为控制方程(47)~(49)与控制方程(50)~(56)之间已经解耦.这时便可以将控制方程(50)~(56)处理为非惯性坐标系中的弹−液耦合动力学问题.这也是飞行器强度计算的一般处理方法.作者专门研究了与控制方程(50)~(56)构成的非保守非线性弹−液耦合动力学控制方程的应用问题,将文献[43-44]的研究推广到非惯性系中的流固耦合问题中.专家评价对这类系统有限元建模、计算及结果分析、讨论具有重要的参考价值.
综合4.3~4.5 节的结果,可以近似的看出非保守非线性刚−弹−液−控耦合动力学控制方程的应用的效果.精确的研究非保守非线性刚−弹−液−控耦合动力学控制方程的应用(解析解),在数学上说是要应用刚−弹−液−控耦合动力学全部控制方程式(47)~(56),这是较为困难的,可以应用较为简单的算例来试探.对于较为复杂的算例,建议应用4.1 或4.2节的有限元法来试探.
5 结论
(1)建立了非保守非线性刚−弹−液−控耦合系统的Hamilton 型拟变分原理和Lagrange 方程,应用系统的Lagrange 方程推导出非保守非线性刚−弹−液−控耦合分析动力学的控制方程.
(2)从Hamilton 型拟变分原理的泛函和应用Lagrange 方程得到的控制方程都说明:刚−弹耦合和刚−液耦合是惯性耦合,弹−液耦合和控−刚耦合是接触耦合.
(3)从两个方面概要地研究了非保守非线性刚−弹−液−控耦合系统的Lagrange 方程的应用.
①应用Lagrange 方程建立了相应的位移协调元和杂交元计算模型,分析了这类计算模型的优越性;
②应用系统的控制方程对实际问题进行解析的分析讨论,说明了应用解析的分析讨论来研究问题与应用数值的、定量的分析方法来研究问题的互补特性.
致谢在完成本文的过程中,得到刚−弹−液−控耦合动力学专家岳宝增教授的热情帮助,作者表示衷心感谢!
