一种结合自适应噪声完备经验模态分解和盲反卷积去除脑电中眼电伪迹的新方法

吴全玉，张文强，潘玲佼，陶为戈，刘晓杰

（江苏理工学院电气信息工程学院生物信息与医药工程研究所，常州，213001）

引 言

脑电（Electroencephalogram, EEG）信号包含丰富的人体生理信息，是实现人机控制系统的新手段[1-3]，但信号的非线性和微弱性导致采集的EEG 信号更容易受到噪声干扰。如果不能充分祛除噪声干扰，后续的EEG 信号分析工作将受到影响，如信号的特征提取[4-5]和信号的分类问题。常见的干扰有设备和交流电造成的工频干扰[6]和高频信号干扰。还有受试者生理状态造成的干扰，如眼电（Electrooculography, EOG）伪迹[7-9]、心电（Electrocardiogram, ECG）伪迹[10-11]和肌电（Electromyogram, EMG）伪迹[12]等。其中工频干扰和高频干扰可通过滤波器进行滤波处理，EMG 和ECG 伪迹与被采集者的人为活动关系密切，采集时多加注意可有效缓解。但由于眼睛运动如不由自主的眨眼等与信号采集装置较近的原因，EEG 信号中常常混有EOG 伪迹，且伪迹幅值较大。此外，与EEG 信号有相重叠的部分，对EEG 信号精度影响也很大。

近几年，随着脑机接口[13-14]技术的发展，出现了许多眼电EOG 伪迹祛除算法，具体可细分为以下3 种方法：回归法、阈值法和时域信号处理方法。回归法不适用于实时EEG 信号中伪迹的祛除，需要分批量的进行伪迹祛除工作，同时在消除EEG 信号中伪迹时，也会造成原本信号的损失。但是回归法定位伪迹准确，与其他方法结合使用，是目前研究的热点。阈值法通过删除幅度超过设定范围的信息，获得无伪迹的EEG 信号，缺点与回归方法相似。时域信号处理方法包括主成分分析（Principal component analysis, PCA）和独立 成 分分析（Independent component analysis, ICA）[15-17]。 Mannan等[18-19]提出的基于回归法和高阶统计的混合ICA 方法成功实现了EOG 伪迹的祛除，保留了原始的EEG 信号数据，但是该方法需要大量先验知识才能确定伪迹成分。Mammone 等[20]提出基于（Wavelet transformation ICA, WT-ICA）的EOG 伪迹分离方法，首先将EEG 信号用母小波分解为若干小波基分量，再设定相关熵值，利用ICA 分析分离小波基分量中的EOG 分量进而重构EEG 信号。该方法计算速度快，但缺点是超完备ICA 问题无法解决，且小波基需要人工选择。黄璐等[21]提出了一种改进极大似然估计的盲反卷积方法用于EEG 信号中的伪迹祛除，该方法对EOG 伪迹分离效果较好，但是先要对观测信号进行InformaxICA 处理，分离时常伴随着数据损失，同时对改进算法性能的评估不足。罗志增等[22]提出基于自适应噪声完备经验模态分解和独立成分分析相结合（Complete ensemble empirical mode decomposition with adaptive noise and independent component analysis, CEEMDANICA）的单通道EOG 伪迹祛除方法。该方法通过ICA 分析，将CEEMDAN 分解EEG 信号所得的多个固有模态函数（Intrinsic mode function, IMF）分量构建为多个源信号，再利用模糊熵公式计算ICA 分析后多个源信号的模糊熵值，最后通过预先设定好的的阈值区分EEG 分量和EOG 分量。该方法在保留了原始信息的同时，需要进行人工干预判断伪迹成分。本文在前人研究的基础上，结合了CEEMDAN方法与目前研究较多的（Blind deconvolution, BD）方法，提出了一种新的CEEMDAN-BD 方法。该方法利用了CEEMDAN 和BD 两种方法的各自优势，在保留原始EEG 信号的基础上，自适应的实现其中EOG 伪迹的祛除，可为EEG 信号的处理和其他人体生理信号处理分析提供一定理论和方法借鉴。

1 算法与评价方法

1.1 CEEMDAN-BD 算法

为快速理解CEEMDAN-BD 算法过程，图1给出算法的流程图，其中原始脑电信号即为采用滤波器处理后含有EOG 伪迹的EEG 信号。使用CEEMDAN 方法对原始脑电信号展开分解，得到N个IMF 分量。将得到的N个IMF 作为BD 卷积模型的观测信号，根据EEG 信号的生理特性，应用盲反卷积BD 的原理，构建源信号由EEG 信号和EOG 伪迹卷积混合而成的模型，再将其转化成瞬时混合模型x(t)=As(t)，其中x(t)表示观测信号，s(t)表示源信号。构建模型后基于EOG 伪迹和无伪迹EEG 信号之间的相互独立性，根据联合块对角化原理和转化为瞬时混合模型的观测信号建立代价函数J(W)。对代价函数J(W)进行共轭梯度法迭代，其中W是矩阵A的逆矩阵。迭代完成获得W的最优值W，再由公式s(t)=Wx(t)分别得出由EEG 信号和EOG 伪迹组成的源信号，成功实现分离。

图1 CEEMDAN-BD 算法流程图Fig.1 Flow chart of CEEMDAN-BD algorithm

1.2 CEEMDAN 分解

CEEMDAN 分解不同于经验模态分解（Empirical mode decomposition, EMD）。传统EMD 分解极易出现模态混叠问题[22-23]，影响分解准确性。为解决这一问题，CEEMDAN 分解加入了高斯白噪声。流程如下：

（1）在观测信号中加入高斯白噪声组成新的构造信号xj(t)=x(t)+σ0wj(t)，其中x(t)为观测信号，σ0为求第1 个模态分量时的噪声标准差，wj(t)为服从N(0,1)分布的白噪声，j=1,2,…,N；

（2）对xj(t)展开N次EMD 分解，得到N个第一阶分量后取均值，得到第一个模态分量即

同时第1 个余量信号r1(t)为

（3）判断余量信号r1(t)的极值点个数是否超过2 个：若是，对EMD 分解到的第1 阶模态算子加入第1 阶余量信号r1(t)构成信号r1(t)+σ1M1[wj(t)]进行EMD 分解得到第2 个模态分量即

式中：σ1表示求第2 个模态分量时的噪声标准差；Ma[·]为对信号进行EMD 分解后的第a个IMF 模态的算子；M1[Wj(t)]为EMD 分解产生的第1 个模态的算子；wj(t)表示第j次分解添加的白噪声。

（4）循环步骤（3），直到前1 层模态分解得到的余量信号的极值点个数不超过2 个，停止分解得到最终的余量信号R(t)，即

式中：K表示模态分解的次数；k表示模态分解的层数，k=1,2,…,K。

原始信号x(t)被分解为

在第k层分解中，计算第k个余量信号rk(t)，即

第k+1 个模态分量为

1.3 构建盲反卷积代价函数

观测信号x(t)=[x1(t),x2(t),…,xK(t)]由 CEEMDAN 方法获得，假设构成观测信号的m维源信号是卷积混合模型[21]。观测信号xi(t)的卷积混合模型为

式中：l表示滤波器的阶数；hij为滤波器矩阵；p=1,2,…,l-1。

设定长度为w的时间窗，且满足Kw≥m(w+l-1)，则t时刻EEG 信号的观测信号xi(t)为

式（9）写成矢量形式可得

此时卷积混合模型用x(t)=As(t)表示，变成瞬时混合模型。矩阵A=(Aij)可表示为

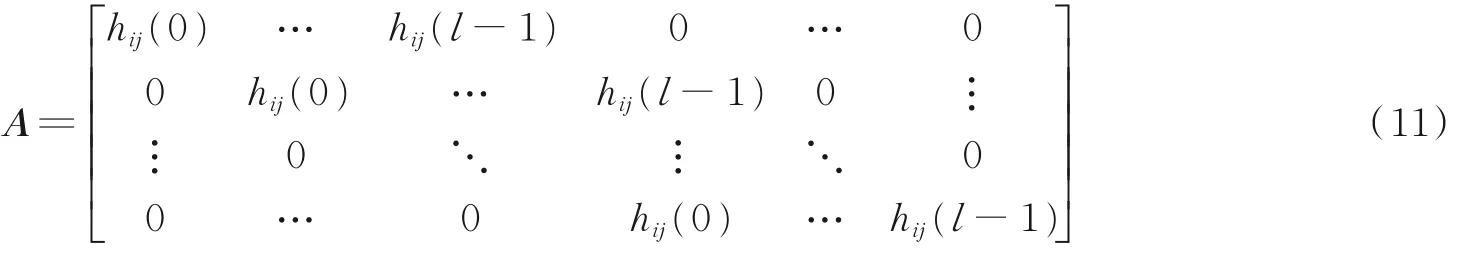
式中：hij为第j个源信号到第i个观测点的卷积混合过程，i=1,2,…,K，j=1,2,…,m。

再根据联合块对角化原理和转化为瞬时混合模型的观测信号建立代价函数J(W)。因为s(t)的自相关矩阵RS(τ)是分块对角矩阵，可表示为

式中τ表示时延，bdiag[·]表示分块对角阵。

观测信号x(t)=As(t)的自相关矩阵Rx(τ)可表示为

使用逆矩阵可表示为

取 多 个 时 延τq，q=1,2,…,Q，求 得 多 个Rx(τq)，建 立 如 式（15）所 示 的 代 价 函 数J(W)，使WRx(τq)WH的非对角块部分趋近零。

式中：||·||F表示矩阵的 Frobenius 范数；W表示混合矩阵A的逆矩阵；τq表示时延，q=1,2,…,Q；在时延τq下，Rx(τq)是x(t)的自相关矩阵，Rx(τq)=ARS(τq)AH；offbdiag 表示矩阵的非对角块结构。

1.4 共轭梯度法

利用共轭梯度法[21]对J(W)进行如式（16）―（18）所示的迭代。

式中：αk为步长因子矩阵，本文通过线性搜索方法确定；矩阵dk和βk由给定d0迭代得到，d0=-g0；gk可由式（19）计算获得。

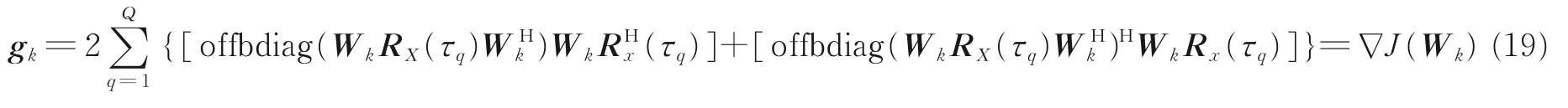
（1）选取逆矩阵W的初始值为W0并标准化处理，取初始值k=0，终止阈值ε＞0；

（2）计算g0=∇J(W0)的值，并令d0=-g0；

（3）根据逆矩阵W的迭代式，计算Wk+1，并进行标准化Wk+1=Wk+1/||Wk+1||F；

（4）判断 |Wk+1-Wk||F≤ε是否成立。若成立，则中止迭代，输出W=Wk+1；

（5）令ndim为逆矩阵W的维数，若k=ndim，取k=k+1，W0=Wk+1跳转到步骤(2)；并分别计算gk+1和dk+1，跳转至步骤(3)。

经过多次迭代获得逆矩阵W的估计值W，再由式s(t)=Wx(t)获得无伪迹的EEG 信号以完成EOG 伪迹分离。

1.5 对比算法

为更好地评价本文方法的客观性能，选择已有的WT-ICA 算法和CEEMDAN-ICA 算法与本文提出的新方法对比分析。WT-ICA 算法[19]采用适用于EEG 信号分析的DB4 母小波对信号进行小波分解，再设置EOG 分量与EEG 分量的区分熵值，通过ICA 对分解后的分量进行EOG 分量分离，最终重新构建无EOG 伪迹的EEG 信号。另外，CEEMDAN-ICA 算法[22]是通过ICA 分析将CEEMDAN 分解EEG 信号所得的多个IMF 分量构建为多个源信号，再引入便于EEG 信号计算的模糊熵公式，获得各个源信号段的模糊熵值。其定义是给定一个模糊集A，并 用 向 量 表 示 为A=[uA(x1),uA(x2),…,uA(xn)]，令则模糊熵定义为最后通过预先设定的阈值判断源信号分量中是否含有EOG 伪迹，将含有EOG 伪迹的分量信号置零，获得无EOG 伪迹的EEG信号。

1.6 评价方法

为有效评价伪迹的祛除效果，并确定祛除伪迹后EEG 信号的原始数据保留程度，引入相关系数R作为评价方法，可表示为

式中：i表示采样点数；x表示原本含EOG 伪迹的EEG 信号；y表示算法运行后的EEG 信号。

2 实验数据

为评价所提出新方法的性能，采用CHB-MIT 头皮脑电数据库[24-25]中的标准EEG 信号进行计算分析。CHB-MIT 头皮脑电数据库信号的采样频率为256 Hz，每个文件包括23 路通道采集的EEG 信号，分辨率为16 bit[26]。CHB-MIT 头皮脑电数据库中23 路通道数据的整体显示情况如图2 所示。

图2 MIT 标准数据库中23 路通道脑电信号Fig.2 EEG signals of 23 channels in MIT standard database

考虑到提出的新算法更偏向于对单通道脑电信号的处理，为此选择MIT 数据库中的一部分数据进行分析研究。根据EEG 信号采集传感器中电极的位置选择FP1-F3 通道的EEG 信号作为实验数据，截取其中10 s 数据如图3 所示，采样点数2 560 个。可以看出信号幅值的最大值都没有超过150 μV，脑电信息中包含较多的高频成分和伪迹，特别是眼电伪迹的幅值较为明显。

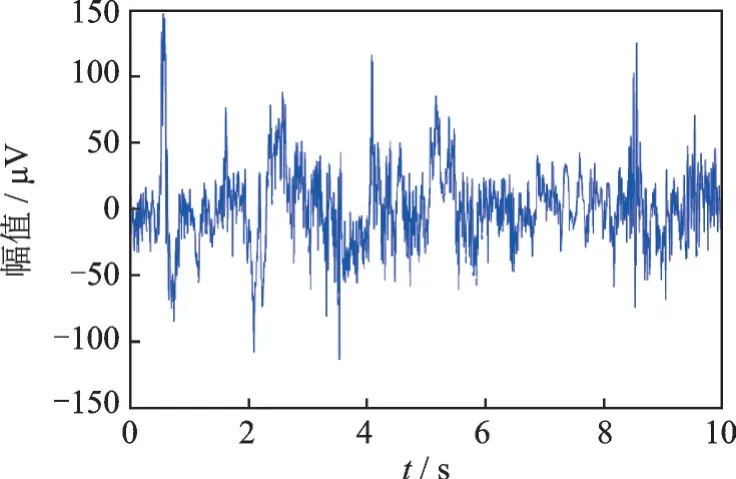
图3 截取的10 s 实验数据Fig.3 Selection of 10 s test data

3 实验研究与结果分析

本文对CHB-MIT 头皮脑电数据库中选定的数据进行EOG 伪迹祛除处理，并与选定的两种算法进行伪迹祛除性能比较分析，来综合评价新提出方法的实用性以及可靠性。

3.1 预处理

由于采集设备和220 V 50 Hz 交流电流的影响，初步采集的EEG 信号中含有工频干扰和高频噪声，可以通过带通滤波器进行过滤。所以在实验开始之前首先要对EEG 信号进行滤波处理。本文对EEG信号进行设定频率为0.5～60 Hz 带通滤波处理。图4 为CHB-MIT 头皮脑电数据库中选定信号进行预处理前后的时域对比结果。从图4 可以看出，处理后的结果明显没有那么多的高频信息，杂波减少较多，如图4 中箭头所示区域。但是眼电EOG 伪迹的幅值几乎没有削弱，说明眼电EOG 伪迹的频率成分没有滤除。分析主要原因可能是眼电EOG 伪迹的频率成分接近脑电成分的频率，不能通过简单的带通滤波器滤除干净。

图4 预处理后的EEG 信号对比结果Fig.4 Comparison results of preprocessed EEG signals

3.2 CEEMDAN-BD 方法眼电伪迹祛除

首先使用CEEMDAN 方法对滤波处理后时长为10 s 的EEG 信号展开分解，分解算法的参数设置为：σ=0.2，N=100，分解后得到的多个IMF 作为BD 卷积模型中的观测信号，分解结果如图5 所示，此时的IMF 中是EEG 信号与EOG 伪迹的混合表现。

设定观测信号由EEG 信号和EOG 伪迹2 个源信号卷积混合而成，混合模型如式（8）所示。设置2 阶FIR 滤波器，取时间窗长度w=6，具体：H=(Hij)12×2，其中，Hij=aij+bij z-1，aij和bij为随机生成系数。

将EEG 信号与EOG 伪迹的混合模型变换为适合计算代价函数的瞬时混合模型x(t)=As(t)。再计算观测信号的自相关矩阵Rx(τ)，使用逆矩阵W进行表示，如式（14）所示。基于此，选取时延τ（qq=1,2,…,Q，Q=20），求得多个Rx(τq)，并建立代价函数J(W)，使得WRx(τq)WH的非对角块部分趋近零。

最后对代价函数J(W)展开共轭梯度法迭代，获得W的最优值W。迭代时取初始值k=0，终止阈值ε=0.01，进而由式s(t)=Wx(t)分别得出由EEG 信号和EOG 伪迹组成的源信号，成功实现分离。从分离结果图6 可以看出，图中多处含有EOG 伪迹较明显的位置，伪迹均有明显消除。对比EOG 伪迹祛除前的EEG 信号，整体波形变化不大，较为接近原始的EEG 信号，没有对数据有作过分的处理，或者出现奇异的变化位置。通过图6 可以看出，选定的EEG 信号数据在1 s，4 s 和5 s 处有明显的眨眼动作伪迹，从算法处理后的图中可以看出眨眼导致的信号幅值没有明显高于周围信号，具体如图6 中箭头所示位置区。

图5 CEEMDAN 分解后多个IMF 分量Fig.5 Multiple IMF components after CEEMDAN decomposition

图6 CEEMDAN-BD 算法处理结果对比Fig.6 Comparison of results processed by CEEMDAN-BD algorithm

3.3 两种对比方法的眼电伪迹祛除效果

图7 展现了使用WT-ICA 算法处理上述相同EEG 信号的结果。在用WT-ICA 算法分解参数设置时，选择适合于EEG 信号分析的DB4 母小波，并且设置分解层的层数为6。

对比图7 可以看出，WT-ICA 算法祛除EOG 伪迹幅值明显，但是对比处理前的原始EEG 信号，祛除后的EEG 信号中成分有明显的缺失，较多的频率成分被删除，同时改变了原始波形的形状，如采样点600 之前，波形变化尤为明显。另外，在采样点1 200 和1 800 附近处，原始脑电信号均有大量的滤除。可见使用WT-ICA 算法对该脑电信号的处理较不理想。

图8 给出了采用CEEMDAN-ICA 算法处理后的结果。CEEMDAN-ICA 算法首先对含有EOG 伪迹的EEG 信号执行CEEMDAN 分解。整个算法CEEMDAN 部分参数的设置与本文中CEEMDANBD 算法的参数一致。从运行结果图中可以看出伪迹祛除后的信号成分无明显缺失，保留了大部分的脑电信息，但伪迹祛除的效果不是特别明显，如采样点2 100 后的EOG 伪迹成分明显滞留。

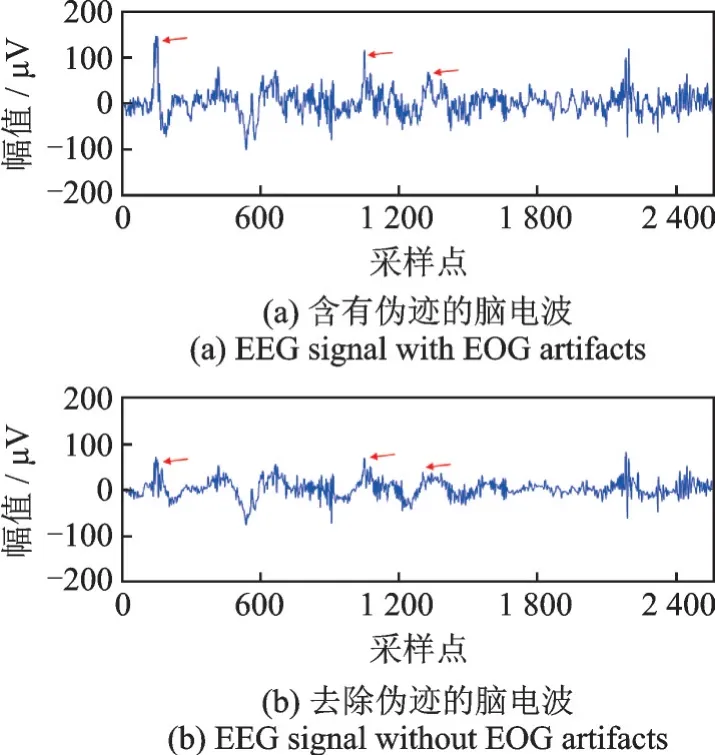
图7 WT-ICA 算法处理结果对比Fig.7 Comparison of results processed by the WT-ICA algorithm

图8 CEEMDAN-ICA 算法处理结果对比Fig.8 Comparison of results processed by the CEEMDAN-ICA algorithm

3.4 相关系数的计算分析

为进一步评价3 种算法对原始脑电信号的保持程度，分别计算出 CEEMDAN-BD 算法、WT-ICA 算法和CEEMDAN-ICA 算法处理后的EEG 与原始EEG 数据的相关系数R，结果如表1 所示。

从表1 可以看出，经过3 种算法处理后数据相关系数的比较，CEEMDAN-BD 算法对于EOG 伪迹的祛除效果最好，并且有效保留了EEG 原始数据中的成分，其相关系数是0.82。通过对比WT-ICA 算法的相关系数是0.64，发现该算法对原始EEG 信号中的有效信息损失较多。这是因为WT-ICA 算法应用到单通道EEG 信号时，经过小波变换后，单通道EEG 信号将被转换成多个小波系数，这看起来满足了ICA 的输入和输出条件，即观察到的信号数不少于源信号。但是包含眼电伪迹的小波系数也包含更多的EEG 有效信号，直接删除包含眼电伪迹的小波系数肯定会导致有用EEG 信号的丢失。同时本文的研究结果证实了前人的研究[8]。另外，经过多次WT-ICA 算法处理对比，还发现该算法的运行结果不稳定。相对于CEEMDAN-ICA 算法，虽然对EOG 伪迹祛除效果微弱，但是该算法整体运行稳定。这是因为CEEMDAN 方法[22]在EEMD 的基础上，通过自适应地加入白噪声，克服了EEMD 在加入白噪声后分解失去完备性以及产生重构误差的问题。根据表1结果所示，CEEMDAN-ICA 算法的相关系数是0.76。可以看出对原始信号进行CEEMDAN 分解后进行ICA 分量重构比先进行小波变换分解，再进行ICA 重构的效果好，能够更好地保留原始EEG 信号信息。

表1 3 种方法相关系数对比Table 1 Correlation coefficients comparison of the three methods

通过3 种算法计算结果的相互比较评价，验证了本文提出的CEEMDAN-BD 算法，与其他2 类算法相比，具有更好的EOG 伪迹祛除效果。

4 结束语

鉴于EEG 信号中EOG 伪迹影响消除问题一直未有效解决，影响将采集的脑电信号用于人们的日常生活，如脑电控制飞行器和脑电控制轮椅等项目。本文提出一种多类型算法融合的自适应噪声完备经验模态分解结合盲反卷积的方法，能够自动用于脑电信号中的EOG 伪迹祛除。采用CEEMDAN 分解将含有伪迹的EEG 信号分解为多个IMF，再利用BD 模型方法将EEG 信号作为卷积及混合的源信号之一分离出来，成功实现伪迹的有效滤除。通过与WT-ICA 算法和CEEMDAN-ICA 算法的实验结果对比发现，本文算法在消除了模态混叠问题影响的同时，能较好地保留EEG 信号中的原始数据信息，还避免了ICA 分析可能出现的超完备问题，为单通道EEG 信号中EOG 伪迹祛除方面的研究提供了新方法。