抽水蓄能机组水泵断电过程中的机组反转问题

李东阔，宫 奎，王康生，秦 俊，张 飞，郭 鹏

(1.国网新源控股有限公司技术中心，北京 100161；2.江西洪屏抽水蓄能有限公司，江西 靖安 330603)

抽水蓄能电站是电力系统调峰填谷、调频调相以及各种备用需求的重要调节方式，对确保电力系统安全稳定运行具有不可替代作用。在电网供电的峰值时，转轮正向旋转在水轮机模式下运行；在电网供电的谷值时，转轮反向旋转在水泵模式下运行。因此，与常规的机组相比，抽水蓄能机组的运行更为复杂。其中，水力机组过渡过程作为抽水蓄能机组稳定运行的参考标准，对指导抽水蓄能机组的稳定运行具有重要意义。

近年来，随着我国抽水蓄能电站的跨越式发展，相关专家在抽水蓄能机组的过渡过程方面开展了大量的工作[1-2]。刘凯华分析了水泵水轮机特性曲线的特有性质和重要的典型过渡过程，发现水泵水轮机的运行工况点不仅与系统的当前输入有关，并且受历史数据的影响[3]。周建中等[4]将多目标智能优化算法应用于抽水蓄能机组的导叶关闭策略优化问题，提出一种综合性能好的关闭策略优化方法。周大庆等[5]对抽水蓄能机组泵工况断电过渡过程进行数值试验，发现叶片吸力面的涡流是造成水击现象的根本原因。常近时[6]提出了一种水泵水轮机装置泵工况断电过渡过程的解析计算方法，能够满足工程的实际要求计算精准度。杨建东等[7]将过渡过程的现场实测压力数据进行处理，揭示了抽水蓄能机组甩负荷过程中压力脉动的成分和相对变化规律。现阶段，大量专家虽对抽水蓄能机组的过渡过程进行了研究，而在水泵断电工况的研究方面，主要通过数值仿真的方式研究其过程中的能量特性和稳定性[8-10]，在一维特征线法方面的研究，主要集中于在三维湍流数值模拟的边界条件引入一维特征线法[1,11-12]，很少有人通过一维特征线法和原型试验[13-15]对水泵断电工况的机组反转问题进行研究。洪屏电站机组调试及竣工验收期间，水泵断电时机组出现了反转，然而相关领域专家对机组是否能够反转以及反转转速数值存在分歧。机组水泵工况断电的反转问题一直存在，如何处理该问题，国内尚未达成共识。尤其在水泵工况断电的关闭规律选取时，机组是否允许反转、反转转速的大小对机组过渡过程的影响规律尚不明确。

本文针对机组反转对抽水蓄能机组的过渡过程影响规律进行探索，建立了洪屏抽水蓄能电站的机组模型，通过模拟计算与原型试验的方式，验证了结果的正确性，并对机组30%反转和100%反转的结果进行分析，探索反转对通道涌流系统压力极值、材料应力极限强度、压力脉动的影响规律，为抽水蓄能机组的水力机组过渡过程的研究提供帮助，为抽水蓄能机组的稳定运行提供参考依据。

1 控制方程及求解方法

1.1 控制方程

抽水蓄能机组的引水系统中管道水流运动控制方程组包括连续方程和动量方程。

连续方程

(1)

动量方程

(2)

式中，α为水击波速；V为水流流速；H为水头；f为管道沿程摩阻系数；D为管道直径。

1.2 特征线法

将式(1)和(2)联合为偏微分方程，为进行抽水蓄能机组中引水系统过渡过程计算分析，主要是计算求解上述方程中的流速V和水头H。对上述方程进行变化

(3)

(4)

则必然存在一个常数k=±a/g，使得下式成立

(5)

由于Q=VA，且管道中的流速远小于水击波速，因此可以转换得到如下常微分方程组。式(6)为正特征方程，式(7)为负特征方程，可通过差分图进行求解。

(6)

(7)

1.3 边界条件

为了求解特征线方程组，我们需要给出管道具体的边界条件才能进行求解。由于抽水蓄能电站的上下游一般都是水库，其引水系统过渡过程时间比较短。因此，在进行计算分析时，保持某一特定值。由于各个管道材料、元件、配置结构均有可能存在不同，要根据不同条件，分别进行设置。针对混合管道方法，可以通过调整波速法实现。

2 洪屏电站过渡过程实例

2.1 基本概况

洪屏电站水泵工况最大净扬程580 m，最小净扬程540 m。输水线路以引水主洞为一洞两机、尾水隧洞也为一洞两机布置。输水系统主要建筑物包括：上库进/出水口、上游闸门井、上游调压室、上竖井、下竖井、下平洞、引水钢岔管、引水高压钢支管、尾水支管、尾水岔管、下游调压室、尾水隧洞、下游闸门井、下库进/出水口等。图1为该电站的输水系统参数建立的过渡过程数值仿真模型。

该电站要求特征参数控制值满足如下条件：机组蜗壳进口最大压力不大于887 m，尾水管进口最小压力不小于0 m，上游调压室最高涌浪不超过757 m，上游调压室最低涌浪不低于688 m，尾水调压室最高涌浪不超过195.5 m，尾水调压室最低涌浪不低于131 m，上游闸门井最高水位不超过 737.9 m，上游闸门井最低水位不低于708.18 m，下游闸门井最高水位不超过185 m，下库闸门井最低水位不低于156.91 m。

图1 电站数值仿真计算模型

本文选取双机切泵工况，该工况上库水位为729.6 m，下库水位169.3 m，两台机组同时抽水断电，导叶正常关闭。本文分别对机组的反转极值为额定转速的30%、100%的工况进行计算(以下简称30%反转、100%反转)，关闭规律如图2所示。

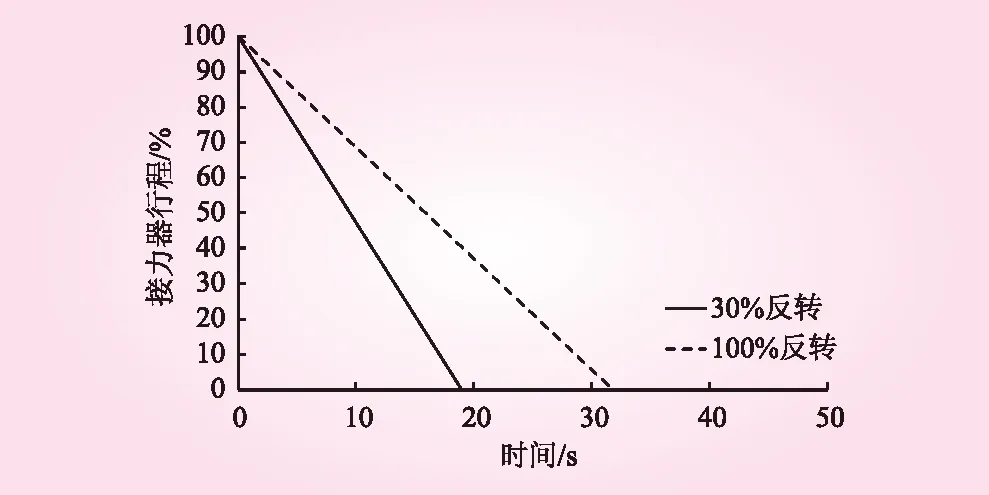
图2 水泵断电工况关闭规律

图3 特征参数的计算值与实测趋势线对比

表1 100%反转特征参数的计算值与实测趋势值对比

2.2 计算结果与试验结果对比

由于本文的工况为双机切泵工况，不属于水力干扰工况，且两台机组的机组性能一致，因此仅对其中一台机组的过渡过程参数进行对比。图3为过渡过程评价参数的计算结果与实测趋势线对比。根据图3a可知，随着时间的变化，蜗壳进口压力呈现先降低后增大的趋势，计算结果趋势与实测趋势线基本一致。由图3b可知，尾水管进口压力呈现先增大后减小的趋势，随后平稳的趋势，结果与实测趋势线基本一致。由图3c可知，机组相对转速的趋势线大致相同，仅在30 s以后，存在细微区别。

表1为100%反转的现场实测值与计算结果对比，由表1可知，尾水管进口最小压力非常接近，相差在1%以内。蜗壳进口最大压力计算值与实测趋势值有相对较大的差异，计算值的结果较高，但有利于实际工程的安全。机组转速变化的计算值也与实测趋势值接近，相差在1%以内。

综上所述，本文的计算值与现场的实测趋势值基本一致，确保了计算的准确性，说明了本文计算结果的准确性。

2.3 30%反转与100%反转对比分析

2.3.1通流系统压力极值

图4为蜗壳进口压力、相对转速变化。定义相对转速为转速与额定转速的比值。由机组相对转速的变化可知，机组相对转速呈现先降低至0%，即机组反转前的过程；随后，机组相对转速增高到反转最高转速，再降低，即机组反转的过程。与此同时，通过对比30%反转和100%反转的参数，发现当机组100%反转时，机组转达到最大反转转速的时间较长。由蜗壳进口压力变化可知，随着时间的改变，两种工况的蜗壳进口压力最大值均小于特征参数控制值要求，即机组蜗壳进口最大压力不大于887 m。通过对比两种工况的蜗壳进口压力波动幅值，可发现当机组100%反转时，蜗壳进口压力波动幅值较小，蜗壳进口压力最大值较小。

图4 蜗壳进口压力、相对转速随时间变化过程

图5为尾水管进口压力、相对转速变化。由尾水管进口压力变化可知，在两种工况下，当机组100%反转时，尾水管进口压力波动幅值较小，尾水管进口压力最小值较大。但两种工况尾水管进口最小压力均达到了特征参数控制值要求，即尾水管进口最低压力大于0。综合对比尾水管进口压力和机组相对转速，可发现两种工况的尾水管进口压力最小值产生在机组反转以后。

图5 尾水管进口压力、相对转速变化示意

图6为机组扭矩、相对转速变化。定义正值扭矩为水泵方向扭矩，负值扭矩为水轮机方向扭矩。由机组扭矩变化可知，30%反转的水泵方向扭矩最大值(5.38×106N·m)和水轮机方向扭矩最大值(0.05×106N·m)小于100%反转的水泵方向最大值(6.48×106N·m)和水轮机方向最大值(0.049×106N·m)。机组水泵断电后，转轮和主轴所受到水轮机方向的最大扭矩小于满载时的工作扭矩(5.38×106N·m)。通过对比两种工况的扭矩变化，可发现当机组100%反转时，作用在转轮和主轴上水轮机方向扭矩的绝对值变小。因此，机组的反转对转轮和主轴的安全性不会产生任何风险影响。

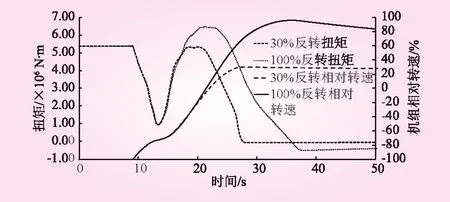
图6 机组扭矩、转速随时间变化过程示意

图7、8分别为上游、下游调压室和闸门井涌浪水位。由图可知，随着水泵断电的发生，30%反转时，上、下游调压室和闸门井的涌浪水位基本重合，100%反转时的下游调压井和闸门井的涌浪水位基本重合，上游调压室和闸门井涌浪水位差的最大值为5 m。通过对比两种工况的参数，发现当机组100%反转时，上、下游调压室和闸门井的涌浪水位的波动幅值越大，波动频率越小。表2为两种工况的涌流极值，表中的控制参数工况为特征参数的控制要求，由表可知，两种反转情况的最高涌浪水位和最低涌浪水位均在控制要求范围内，满足涌浪水位要求。

图7 上游调压井、闸门井随时间变化过程

图8 下游调压室、闸门井涌浪水位

表2 上下游调压室、闸门井涌浪极值

2.3.2材料应力极限

机组水泵断电后，水轮机方向的扭矩主要作用于转轮和主轴上，作用于主轴上的扭转力最大。而扭转应力在横截面上产生剪切应力，在弹性范围内，圆柱形横截面上的扭转应力是沿圆形截面的轴由中心向外表面直线增加的。根据式(8)、(9)可获得主轴上的最大切应力。两种情况下，水轮机方向的最大扭矩、最大切应力如表3所示。洪屏电站水轮机主轴的最小断面直径为0.98 mm，材料的许用扭转切应力为40 MPa[16-17]。由表3可知，30%反转的最大切应力小于100%反转的最大切应力，而两种情况下的最大切应力均小于材料的许用扭转切应力。因此，这两种情况的机组反转不会对主轴产生安全风险。

(8)

(9)

式中，T为主轴上的扭矩；WP为抗扭矩系数；D为主轴直径，该电站的最小断面主轴直径为0.98 m。

表3 水轮机方向的最大扭矩、最大切应力

2.3.3压力脉动

通过原型试验的方式，对洪屏电站的水泵断电过程中30%反转和100%反转的工况进行数据测量，得到了30%反转、100%反转的蜗壳进口和尾水管进口的压力值，随后进行处理，获得压力脉动[18-19]。

图9为蜗壳进口压力脉动，通过对比两种工况的蜗壳进口压力脉动，可发现当机组100%反转时，蜗壳进口压力脉动的最大幅值较小。两种工况的脉动幅值最终趋于相同。与此同时，由压力脉动剧烈波动持续的时间可知，当机组100%反转时，剧烈波动持续时间较短。图10为尾水管进口压力脉动。通过对比两种工况的蜗壳进口压力脉动，可发现当机组100%反转时，尾水管进口压力脉动的最大幅值较高。两种工况的脉动幅值趋于相同。由压力脉动剧烈波动持续的时间可知，当机组100%反转时，反转达到最小波动的时间较短，且维持剧烈波动的时间也短。虽然100%反转脉动的最大幅值相对较大，但与30%反转脉动的最大幅值相比，幅值差别较小，而剧烈波动时间远小于30%反转的剧烈波动时间。

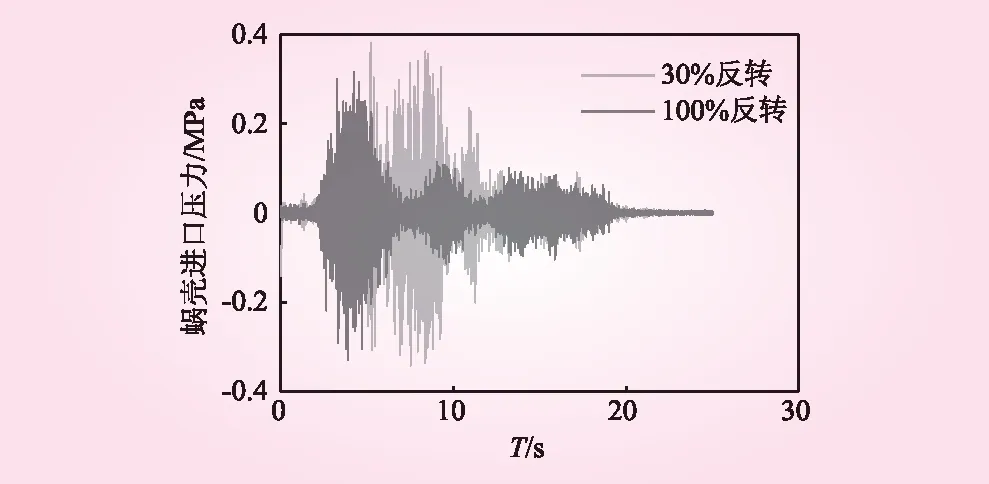
图9 蜗壳进口压力脉动

图10 尾水管进口压力脉动

综上所述，虽然30%反转尾水管进口的压力脉动最大幅值低于100%反转的压力脉动最大幅值，但是30%反转蜗壳进口的压力脉动最大幅值低于100%反转的脉动最大幅值，且30%反转的剧烈波动时间均比100%反转的剧烈波动时间长，不利于抽水蓄能机组的水泵断电工况。

3 结 论

为了探索抽水蓄能机组过渡过程中机组反转对过渡过程的影响规律，以洪屏电站的双机切泵工况机组的试验值和计算值进行对比分析，验证了计算方式的正确性。在此基础上，以双机切泵工况的机组30%反转和100%反转的工况进行模拟计算，对30%反转和100%反转的通流系统压力极值、材料应力极限的计算结果，压力脉动的原型试验结果进行对比分析，结果表明：

(1)通过对比30%反转和100%反转的同流系统压力极值可发现，当机组100%反转时，蜗壳进口压力最大值也较小，尾水管进口压力最小值较大；作用在转轮和主轴上的水轮机方向扭矩的绝对值较大，但转轮和主轴所受到水泵方向的最大扭矩的绝对值均小于满载时的工作扭矩；上、下游调压室和闸门井的涌浪水位的波动幅值较大，但波动频率较小。

(2)在材料确定的情况下，30%反转的最大切应力要小于100%反转的最大切应力，且都小于许用切应力。

(3)通过分析原型试验的数据发现，虽然30%反转尾水管进口的压力脉动幅值低于100%反转的幅值，但是30%反转蜗壳进口的压力脉动幅值低于100%反转的蜗壳进口的压力脉动幅值，且30%反转的压力脉动波动时间均比100%反转的波动时间长，不利于电站的水泵断电过程。

(4)100%反转工况在蜗壳进口压力最大值、尾水管进口压力最小值、压力脉动这3个关键性参数方面，优于30%反转工况。虽然30%反转工况在机组扭矩、材料应力极限等方面优于100%反转工况，但是100%反转工况也符合工程要求。因此，在反转转速不超过额定转速时，机组反转的转速越高，越有利于机组水泵断电工况的过渡过程要求。