单吸式清水离心泵内部水流流动特性数值模拟

2020-08-11王欣永李永业张海赟

水力发电 2020年5期

王欣永，李永业，张海赟，王谦，陈卓

(太原理工大学水利科学与工程学院，山西太原 030024)

0 引言

单吸清水离心泵作为一种流体机械，在工业、农业及国防等各领域有着广泛应用。近年来，随着流体测试技术的发展，水泵内部水流的流动特性的测试手段也由接触式测量发展到了非接触式测量，试验测试方法的发展为人们通过研究离心泵内部水流流动情况来判断离心泵结构设计的合理性和科学性提供了可能。但这些测试手段在试验中仍存在较多困难，需要大量地人力物力和熟练的实验技术。随着计算机技术的不断发展以及数值模拟理论的不断完善，促使人们开始采用数值模拟的手段来研究离心泵内部的水力特性。该研究方法在很大程度上补充了实验手段不足的缺陷。数值计算方法开始广泛用于预测叶轮内的流动，对于人们认识和掌握离心泵内部复杂的三维液体流动及优化和改善离心泵工作性能具有一定的实用意义。

李文广[1]采用PHOENICS程序对二维后弯叶片离心叶轮和三维扭曲叶片离心泵叶轮输送水时，最优工况下离心泵内部水流的流动特性进行了模拟研究，并与试验结果进行了对比分析，论证了该模拟方法的可行性；唐辉等[2]、Dai等[3]、Schmidt等[4]对离心泵内部水流的流动速度及压力特性进行了分析，发现了流动冲击及二次流等流动现象，对于优化离心泵的工作性能具有一定的参考价值；陈池等[5]对离心泵叶轮内的水流流动特性计算，采用椭圆型微分方程法自动生成三维贴体网格，该自动生成网格技术可以满足网格的非均匀性和人为调整网格大小等条件；周岭等[6]利用Fluent软件模拟研究了不同级数深井的离心泵模型的工作性能，并将模拟计算得到的离心泵扬程和效率随流量的变化结果与试验结果进行了对比，吻合性较好；沈艳宁等[7]通过Fluent软件模拟预测了9台模型泵的工作性能，并采用正交试验法对模拟的预测结果进行了设计，分析了影响复合叶轮离心泵各性能指标的及和参数，得出了最优的模型泵设计方案；崔宝玲等[8]对具有前置诱导轮的高速离心泵内的湍流特性进行了试验研究，并对无诱导轮、单个及串联诱导轮3种不同工况下的离心泵性能及汽蚀特性进行了分析；王洋等[9]采用加大流量法和堵塞流道法相结合的设计理念，有效改善了无过载离心泵的工作性能。李晓俊等[10]、Nilsson等[11]等通过计算流体力学方法，采用结构化网格模拟研究离心泵内部的湍流特性，并与试验结果进行了对比，吻合较好，说明该模拟方法是可行的。但目前CFD数值模拟技术对水泵特性的研究，尤其是对于叶轮转动多采用滑移网格和MRF(多旋转坐标系)，而对于模拟时采用动网格技术相对研究的较少。本文将采用动网格技术对水泵的运行工况进行模拟，为水泵参数预测及结构优化提供参考。

1 控制方程

1.1 计算流体力学控制方程

本文基于连续性方程、雷诺时均N-S动量方程和RNGk-ε方程及SIMPLEC算法，使用FLUENT软件进行数值模拟计算，控制方程如下

(1)

动量方程

(2)

k方程

(3)

ε方程

(4)

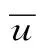
1.2 动网格流场计算方程

对于任意控制体积V上的一般标量φ的守恒型方程为

(5)

其中，

(6)

式中，n为时间层，体积变化由下式求得

(7)

式中，nf为控制体积上控制面的数量；δVj为j控制面在时间步Δt内扫过的体积。

2 模型建立与求解

2.1 模型建立

为了研究水泵内部流场和压力场的分布，需要对单级自吸式离心清水泵进行三维建模，整个模型由四部分组成，分别为水泵进口、蜗壳区、叶轮区以及水泵出水管，该水泵型号为IS65-50-160，离心泵模型如图1所示。

图1 离心泵模型示意

2.2 网格划分和定解条件

在数值模拟之前，首先要进行网格划分，网格化分的质量对模拟结果的精度和收敛性有直接影响。而在网格划分时首先要将计算区域离散化，然后再用Gambit前处理软件进行划分。考虑到离心泵模型结构的复杂特征，本文在网格划分时，采用多层次的结构化和非结构化相结合的划分方式。具体的计算网格如图2所示。

图2 计算网格

为了提高模拟计算的精度，需对叶轮的周围进行局部加密。而在远离叶轮的区域，网格布置较稀疏。叶轮周围的网格大小为0.001 m，在流域的其他区域网格大小为0.003 m，计算区域内的网格数目为623 521。为了更好的实现动网格模拟的研究，减小网格变形，本文采取三角形网格进行加密。在动网格设置中选择弹簧光滑模型和局部重构模型。

本文选用的求解器为分离式求解器。模型入口的边界采用流速入口条件(velocity-inlet)；出口边界采用自由出流边界(OUTFLOW)；叶轮部分布尔运算采用SPLITE，为实现动网格运动奠定基础。调用叶轮转动的UDF程序实现叶轮的匀速转动。动网格的网格运动方式采取弹簧光滑模型和局部重整网格两种方式。运动刚体为Impeller Spin，旋转的运动重心为(0.00，0.00，0.00)。由于叶轮的转动角速度为151 rad/s，最大运动速度为15 m/s，因此，时间步长为0.000 01 s。离心泵不能反转，角速度的方向以右手准则为准。

3 计算结果分析

本文分别对不同流量工况下，离心泵的扬程、效率、流场以及压力场进行分析。

3.1 扬程与效率的计算

表2为单吸式清水离心泵扬程的模拟结果，从中可以看出，随着流量的增大，单吸式清水离心泵扬程都呈现减小的变化趋势其原因主要是在模拟计算时过流部件粗糙表面所引起的摩擦损失和泄漏引起的容积损失没有考虑。

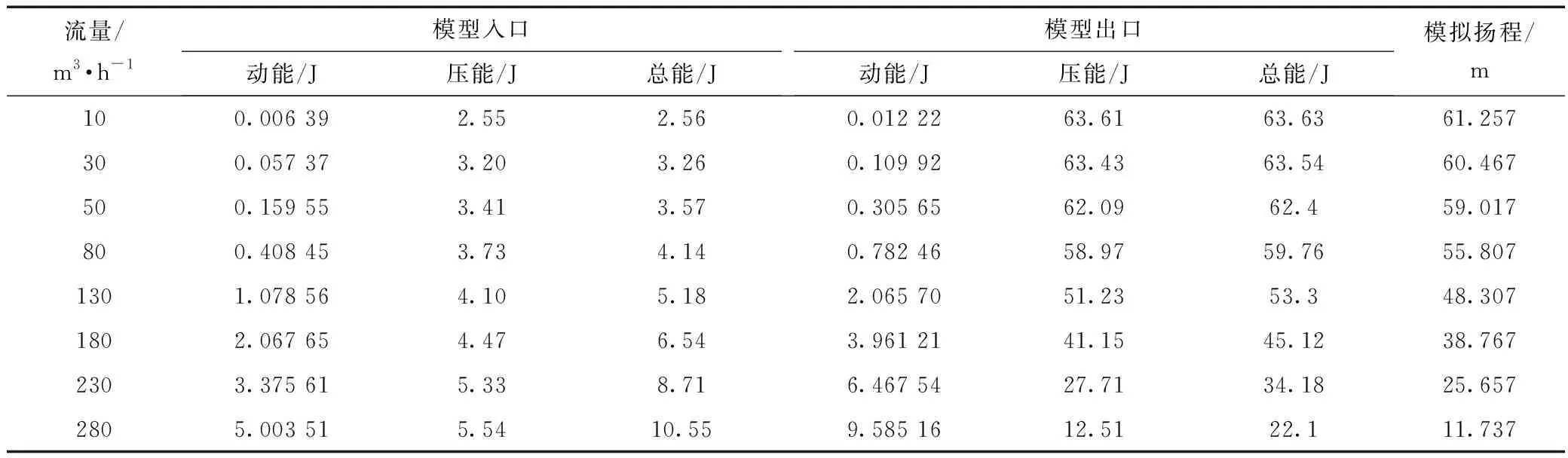
表2 单吸式清水离心泵的扬程模拟值

根据单吸式清水离心泵水力效率的计算公式

η=ρgQH/Mω

(8)

式中，Q为流量；H为扬程；M为旋转轴的总力矩；ω为叶轮的旋转角速度。计算得到不同流量下离心泵的水力效率，具体见表3。

表3 离心泵模拟效率

从表3可以看出，单吸式清水离心泵的模拟效率随着流量的增大都呈现出先增大后减小的变化趋势，其原因主要是由于模拟时叶轮与泄漏液体之间的圆盘摩损、泵轴承填料函中的机械摩损及泄漏引起的容积损失等没有考虑。

3.2 水泵内部压力场

图3为不同流量条件下的离心泵压力场分布，从图3可以看出：①不同流量下离心泵内部叶轮各流道内流体的压力都是在在叶轮的中心位置处最小，在叶轮的出口位置处最大；②叶轮转动的过程中，叶片非工作面的压力要低于工作面，而且在叶片的非工作面容易形成低压区，导致叶片的非工作面气蚀较为严重。③叶轮内的静压分布与总压分布受蜗壳影响都呈现出明显的非对称性，而且靠近蜗壳出口位置流道内的压力分布明显不同于其他流道，压力的最低值出现在靠近蜗壳出口的叶轮流道内。同时随着叶轮的旋转，各流道内的压力都呈现明显的周期性变化。④叶轮出流受蜗壳影响，在其正背面间形成了小漩涡，使得其局部总压显著降低。

3.3 水泵内部流速场

图4为不同流量条件下的单吸式清水离心泵内的流速场分布，从图4可以看出：①叶轮内无明显的流动分离现象，沿流道叶轮内流体的速度在中心位置处最小，在叶轮出口位置处最大，而在蜗壳外周的速度又降到最小。②叶轮转动过程中，叶轮工作面的速度略高于非工作面的流速。③叶轮出流受蜗壳壁面的堵塞影响，使其内部的流动呈现出明显的非对称性，而且在蜗壳出口附近，叶轮流道内流体速度达到最大值。

图3 不同流量条件下的单吸式清水离心泵压力场分布

图4 不同流量条件下单吸式清水离心泵流速场分布

图5 不同流量条件下单吸式清水离心泵内的叶轮压力场分布

3.4 叶轮压力分析

图5为不同流量条件下单吸式清水离心泵内的叶轮压力场分布，从图中可以看出：①叶轮所受的压力较为一致，按照对称分布，叶轮中心处的压力最小，叶轮的出口处压力最大。其原因主要是越靠近叶轮的出口流场的流速较大，叶轮所受的压力就越大；②在叶轮的出口处的正背面出现一个低压区，这主要是由于受到蜗壳以及叶轮构造的影响，叶轮的出口端部形成漩涡。