利用SAS软件实现单因素方差分析方法及比较
2020-08-11孙丽环
孙丽环
(安徽理工大学 数学与大数据学院,安徽 淮南 232001)
SAS(Statistics Analysis System)软件是当今国际上最著名的三大数据分析软件之一,具有强大的数据管理与分析功能,广泛应用于教育、经济、医学等各个领域。方差分析是科学研究中经常需要使用的统计方法之一。利用方差分析可以研究一个或多个因素对试验过程中某项指标的影响因素,并比较因素的各个水平之间是否有显著差异[1-8]。目前发表的文献主要研究的是SAS软件在多因素方差分析中的应用,单因素方差分析应用的文章也有发表,但是文献上没有标明程序运行的代码。本文主要介绍针对单因素方差分析的不同情形,利用SAS软件的相应程序实现单因素方差分析的方法及各个方法之间的比较。
1 例题与相关结论
例1:现对甲乙两车间工人完成某项工艺时间进行抽样统计,其基本情况如表1所示,试分析在95%的置信度下甲乙两车间工人的工作效率是否有显著差异[4]。

表1 甲乙两车间工人工艺完成时间统计
方法一:经分析知,本例需要对两个独立样本的均值做假设检验,以检验两个样本均值是否具有显著差异。现通过下面的T检验程序进行假设检验。程序如下:
data test;
inputa$b@@;
cards;
甲 30.1 甲 28.9 甲 29.5 甲 30.7 甲 31.0
甲 30.6 甲 33.3 甲 29.7 甲 32.4 甲 30.4
乙 29.7 乙 28.7 乙 30.2 乙 31.9 乙 32.8 乙 33.2 乙 31.6
乙 30.2 乙 29.8 乙 30.3
;
run;
proc ttest data=test;
classa;
varb;
run;
执行上述程序后,我们先得出变量满足方差齐次性检验(P=0.7817),故可以用TTEST过程进行方差分析,程序运行的结果可信。在SAS系统中将输出如表2所示的T检验结果,其P值大于0.05,接受原假设,故认为两个独立样本均值没有显著差异。

表2 T检验结果表
方法二:用ANOVA过程进行方差分析,其程序如下:
data test;
inputa$b@@;
cards;
甲 30.1 甲 28.9 甲 29.5 甲 30.7 甲 31.0
甲 30.6 甲 33.3 甲 29.7 甲 32.4 甲 30.4
乙 29.7 乙 28.7 乙 30.2 乙 31.9 乙 32.8 乙 33.2 乙 31.6
乙 30.2 乙 29.8 乙 30.3
;
run;
proc univariate data=test normal plot;
var b;
histogram b;
run;
proc anova data=test;
class a;
model b=a;
means a /hovtest;
run;quit;
执行上述程序后,我们得出变量b满足方差齐次性检验(P=0.7284),故可以用ANOVA过程进行方差分析,程序运行的结果可信。在SAS系统中将输出如表3所示的单因素方差分析的结果表,其P值大于0.05,所以接受原假设,认为两个独立样本均值没有显著差异。ANOVA过程单因素方差分析的结果如表3所示。
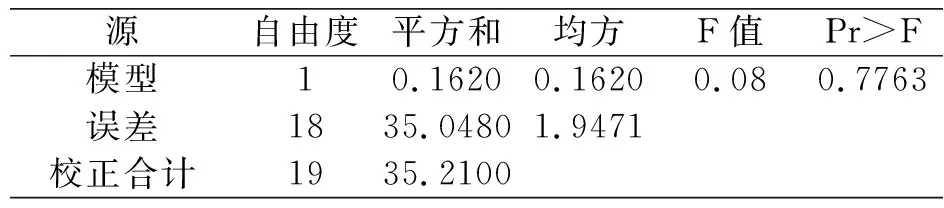
表3 基于ANOVA过程单因素方差分析的结果表
方法三:用GLM过程进行方差分析,其程序如下:
data test;
inputa$b@@;
cards;
甲 30.1 甲 28.9 甲 29.5 甲 30.7 甲 31.0
甲 30.6 甲 33.3 甲 29.7 甲 32.4 甲 30.4
乙 29.7 乙 28.7 乙 30.2 乙 31.9 乙 32.8 乙 33.2 乙 31.6
乙 30.2 乙 29.8 乙 30.3
;
run;
proc univariate data=test normal plot;
varb;
histogramb;
run;
proc glm data=test;
classa;
modelb=a;
meansa/hovtest;
run;quit;
执行上述程序后,在SAS系统中将输出如表4所示的部分主要结果,其P值大于0.05,所以接受原假设,认为两个独立样本均值没有显著差异。

表4 基于GLM过程单因素方差分析的结果表
通过例1,我们得出这样的结论:进行方差分析时仅有一个因素且该因素仅含两个水平,上述三个过程步得到的结果一致。
例2:不同氮肥处理下水稻单产(亩/kg),试通过方差分析研究不同氮肥处理是否对水稻产量有显著影响[4]。

表5 不同氮肥处理下水稻单产
解:该例题问题中仅有一个因素,该因素包含的水平数为4个。此时若采用PROC TTEST,则需要进行多次的两两比较,这会大大增加犯第一类错误的概率。因此,在这种情形下,不宜使用PROC TTEST,可以考虑采用PROC ANOVA或者PROC GLM。二者区别是PROC ANOVA是专门针对均衡数据的试验而设计的。两种方法程序如下:
方法一:ANOVA过程
data test8_1;
inputtreatment$x@@;
cards;
N0 490.4N0 487.5N0 496.4
N1 500.2N1 510.2N1 505.4
N2 509.5N2 510.3N2 507.3
N3 523.1N3 515.7N3 518.9
;
run;
proc univariate data= test8_1 normal plot;
varx;
histogramx;
run;
proc anova data= test8_1;
classtreatment;
modelx=treatment;
meanstreatment/hovtest;
meanstreatment/t;
run;quit;
执行上述程序后,我们得出变量x满足方差齐次性检验(P=0.3559),故可以用ANOVA过程进行方差分析,程序运行的结果可信。在SAS系统中将输出如表6所示的单因素方差分析结果,其P值小于0.05,所以拒绝原假设,即认为不同氮肥处理对水稻产量有显著影响。
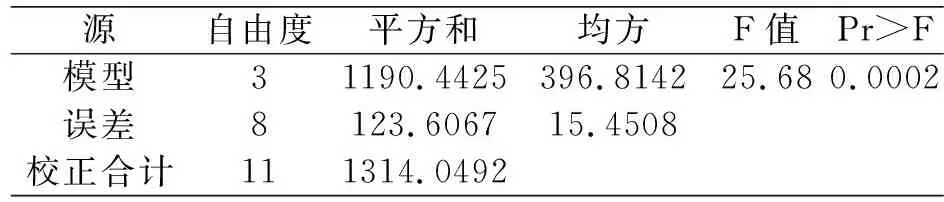
表6 基于ANOVA过程单因素方差分析的结果表
方法2:GLM过程
data test8_1;
inputtreatment$x@@;
cards;
N0 490.4N0 487.5N0 496.4
N1 500.2N1 510.2N1 505.4
N2 509.5N2 510.3N2 507.3
N3 523.1N3 515.7N3 518.9
;
run;
proc univariate data= test8_1 normal plot;
varx;
histogramx;
run;
proc glm data= test8_1 plots(only)=diagnostics;
classtreatment;
modelx=treatment;
meanstreatment/hovtest;
meanstreatment/t;
run;quit;
执行上述程序后,在SAS系统中将输出如表7所示的结果,其P值小于0.05,与ANOVA过程分析的结果相同。

表7 基于GLM过程单因素方差分析的结果表
两个程序运行的结果相同。但是,由于考虑了数据的均衡性,PROC ANOVA在处理均衡数据试验时一般会比PROC GLM更快、占用的存储空间更小(尽管每次运行的时间不一样,但是总体而言PROC ANOVA在处理均衡数据试验时一般会比PROC GLM更快、占用的存储空间更小)。
例3:在食品质量检测中,对4种不同品牌腊肉的酸价进行了随机抽样检测,结果如表8所示,试分析4种不同品牌腊肉的酸价指标有无差异[9]。
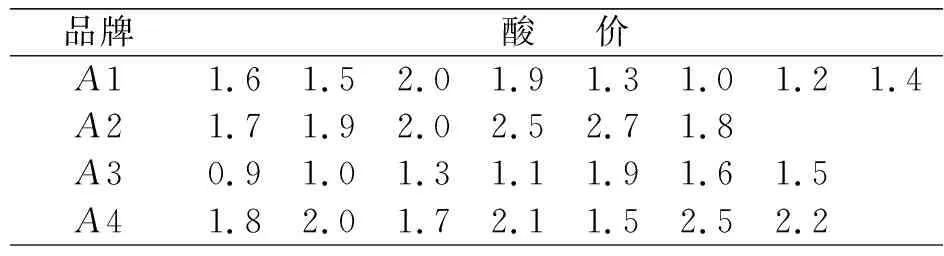
表8 4种品牌腊肉的酸价检测结果
data aa;
inputtypes$x@@;
cards;
A1 1.6A1 1.5A1 2.0A1 1.9A1 1.3A1 1.0A1 1.2A1 1.4
A2 1.7A2 1.9A2 2.0A2 2.5A2 2.7A2 1.8
A3 0.9A3 1.0A3 1.3A3 1.1A3 1.9A3 1.6A3 1.5
A4 1.8A4 2.0A4 1.7A4 2.1A4 1.5A4 2.5A4 2.2
;
run;
proc glm data=aa plots(only)=diagnostics;
classtypes;
modelx=types;
meanstypes/hovtest;
meanstypes/t;
run;quit;
执行上述程序后,在SAS系统中将输出如表9所示的部分结果,其P值小于0.05,拒绝原假设,即认为4种不同品牌腊肉的酸价指标有差异。

表9 基于GLM过程单方差分析的结果表
对于非均衡数据单因素方差分析,采用GLM过程。此外,GLM过程提供了更多的图像输出选项供用户使用[5]。
2 结论
单因素方差分析时,若该因素仅含两个水平,三个过程步PROC TTEST、PROC ANOVA和PROC GLM得到的结果一致;若该因素包含的水平数为3个或者3个以上,可以采用PROC ANOVA或者PROC GLM。二者区别是PROC ANOVA是专门针对均衡数据的试验而设计的。
