一种图像小波去噪的改进阈值函数*
2020-08-11黎彪刁燕罗华徐明
黎彪 刁燕 罗华 徐明
(四川大学机械工程学院 成都 610065)
1 引言
数字图像是由光线通过镜头折射到传感器上产生模拟信号,再将模拟信号转换成数字信号,数字信号传输回主机设备上得到[1]。在这个过程中,恶劣环境、不佳光线和数据转换传输时丢失部分等,都会产生噪声,对获得的图像质量造成严重影响。因此,图像去噪是图像预处理的一个重要部分[2~4]。
一直以来,研究人员提出了许多去噪方法。频域去噪因其将图像变换到频域,处理后再逆变换回空域,可以在很大程度上保留原始图像的细节而备受关注。常见的频域变换方法有傅里叶变换和小波变换[5]。相比傅里叶变换,小波变换不仅保留图像的频率信息,还保留了图像的空间信息,故近十年来成为图像处理的重要工具[6~7]。最早的小波阈值去噪方法是由斯坦福大学的D.L.Donoho提出,使用硬阈值和软阈值函数[8]。但硬阈值函数不连续,会导致去噪后图像出现振铃、伪吉布斯现象;软阈阈值连续却在较大系数上有恒定偏差,会导致去噪后图像出现严重失真[9]。一些典型的改进阈值函数[10~12]在这两个问题上有所改善,却仍有不足。基于小波去噪原理和对传统阈值函数的分析,本文提出一种改进的阈值函数,其在实数域内连续可导,更加光滑,在较大小波系数上保持一致,减少失真。仿真实验验证了改进阈值函数的去噪有效性。
2 小波阈值去噪方法
2.1 去噪原理
假设观测到含噪声的图像信号:
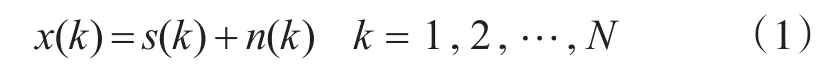
其中:s为原始图像信号,在某些小波基下可以稀疏表示;噪声n服从某一分布;N为信号长度。
小波变换是线性变换,因此小波变换:
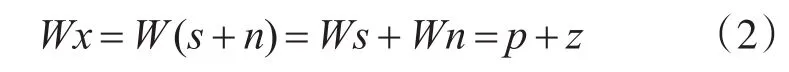
其中:p为原始信号的小波级数,大部分系数是等于零或接近零;z为噪声的小波级数。在和的小波级数系数中,幅值较大的小波系数主要来自原始图像信号,幅值较小的小波系数主要来自噪声[13~14]。所以选取合适的阈值函数,将幅值较大的小波系数轻微减小,将幅值较小的小波系数尽量置零,得到新的小波系数,小波逆变换后就可得到去噪图像。
2.2 经典阈值函数
硬阈值函数和软阈值函数在小波去噪中应用最广。设是观测图像的小波变换系数,是值为水平方向H、竖直方向V或对角方向D的上标,j是小波分解层数;是某阈值;是阈值函数得到系数。硬阈值函数:
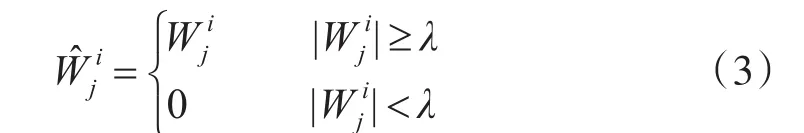
在λ处不连续,会导致小波逆变换后的图像出现振铃、伪吉布斯现象。软阈值函数:
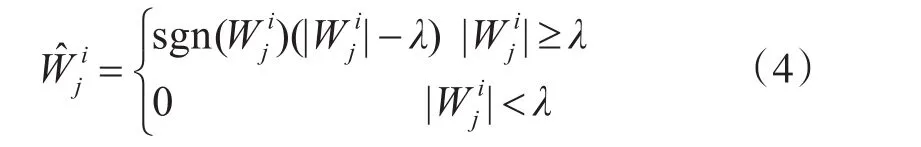
在λ处连续,但大于λ的小波系数都有恒定偏差,包括原始图像信号的小波系数,使小波逆变换的重构图像失真。当数如图1所示,横坐标是观测到的含噪图像小波系数,纵坐标是阈值函数变换后的修改小波系数。
针对硬软阈值函数的问题,国内外提出了一些改进阈值函数,典型的包括折中阈值函数、双变量阈值函数和指数阈值函数等。折中阈值函数[10]:
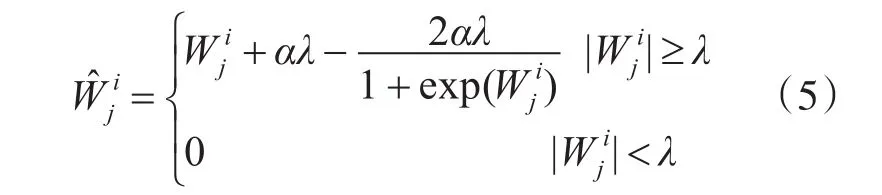
其中:α∈[0,1]。α可以调整软阈值方法的偏差,但随着增大,偏差会越来越大;且函数在λ处不连续,会导致图像失真。当λ=4,α=0.5时,函数如图2所示。双变量阈值函数[11]:


图1 硬软阈值函数
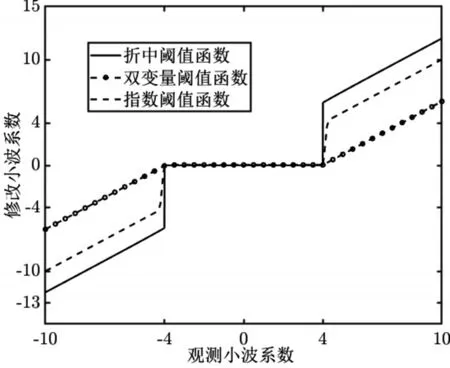
图2 一些改进阈值函数
指数阈值函数[12]:
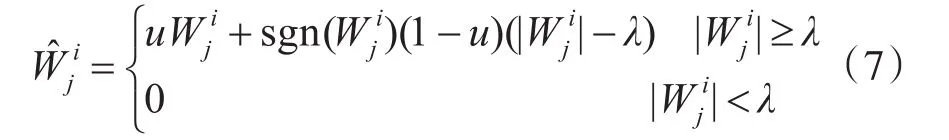
3 改进小波阈值函数
3.1 改进的阈值函数
为了克服以上方法的缺点,本文在上述去噪函数的基础上,提出一种改进函数:
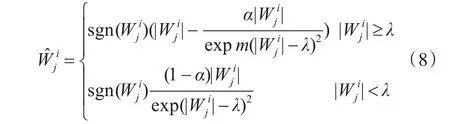
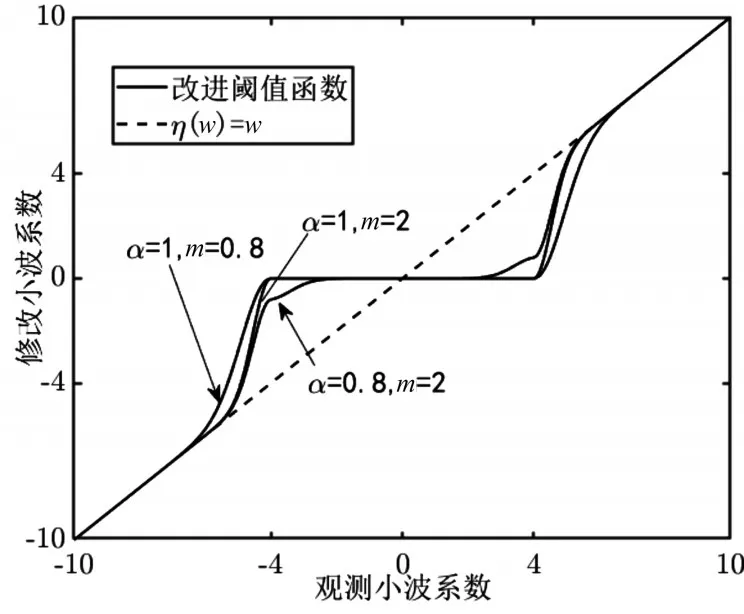
图3 提出的改进阈值函数
3.2 改进的阈值选取
阈值函数中λ的取值对最后去噪效果有着重要影响,λ应该能够最大程度上分离噪声的小波系数和原始图像信号的小波系数。通用阈值是最常用的取值方法,公式为,σ为噪声标准差,N为信号长度。随着小波分解层数增加,噪声所在的小波系数区域应该逐渐减小,在较高层次分解的小波系数大部分都是来自原始图像信号。为了更好分离噪声和原始图像信号,需要在分解层数增加时减小阈值λ。本文改进的阈值选取表达式为
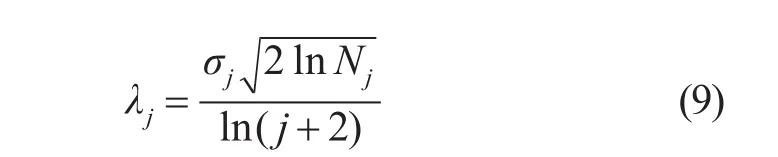
4 实验对比分析
为了说明改进阈值函数在图像小波去噪时的有效性,本文使用Matlab2018软件进行仿真验证。测试图像为标准测试图像[15]中的Baboon图像、Camera图像和Peppers图像。Baboon图像具有高频细节,Camera图像和Peppers图像具有低频细节。给原始标准图像添加密度为0.05的椒盐噪声和标准差为35的高斯白噪声,作为观测到的含噪图像。对含噪图像选择小波基和分解层数进行小波分解,阈值函数变换后进行小波逆变换得到去噪图像。本文采用去噪效果较好的db4小波基,分解层数为3层。提出的改进阈值函数的参数设为α=0.9,m=2。去噪结果如图4~5所示。
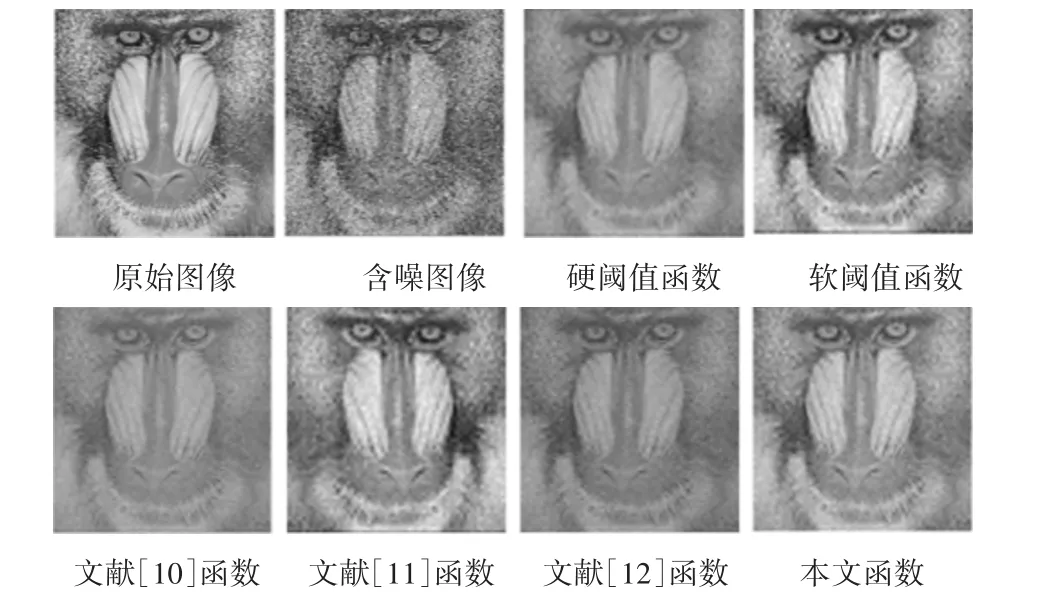
图4 Baboon图像去噪结果

图5 Camera图像去噪结果
从实验图像中可以看出:改进阈值函数的去噪效果视觉上更好。为了进一步比较去噪效果,本文使用均方根误差(RMSE)、信噪比(SNR)和峰值信噪比(PSNR)作为评价标准,表达式:
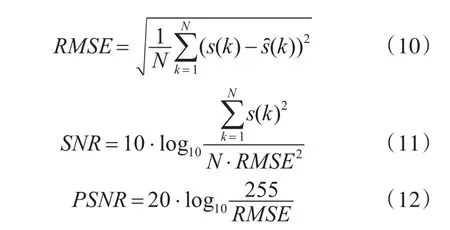
其中:s为原始标准图像,s^为去噪图像,N为总像素数。RMSE越小,SNR越大,PSNR越大,则去噪效果越好。去噪结果如表所示。

图6 Peppers图像去噪结果

表1 Baboon图像去噪结果评价
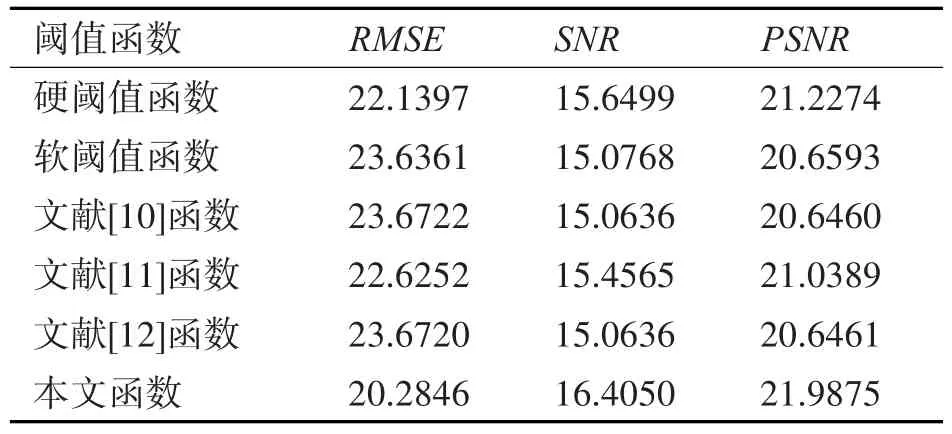
表2 Camera图像去噪结果评价

表3 Peppers图像去噪结果评价
5 结语
根据小波去噪原理,分析小波去噪的传统阈值函数和几种典型阈值函数后,提出一种改进的在阈值处可导的阈值函数。从仿真实验结果中可知,在低频和高频细节图像中,改进阈值函数都获得更好的去噪效果。改进阈值函数在实数域内连续可导,有助于自适应阈值选取研究,有助于小波去噪在图像去噪中的发展和应用。
