基于小波变换和样本熵的脑电信号癫痫特征提取*
2020-08-11宋玉龙
宋玉龙 赵 冕 郑 威
(江苏科技大学电子信息学院 镇江 212003)
1 引言
癫痫是由大脑神经元异常同步化放电所导致的一种慢性神经系统疾患。在临床上表现为突然、短暂的运动,以及感觉、意识、行为、自主神经或精神症状等异常[1~2]。癫痫发作给患者带来了严重的身心伤害,还可能会导致残疾,严重者危及生命。诊断癫痫疑似患者的最有效的方法是脑电图检查。癫痫发作时,脑电活动的复杂性将会降低,主要特点是幅值较高的阵发性的瞬态波形。因此,癫痫脑电特征信号的提取、分析研究,对预防癫痫发病,以及患者的治疗和康复具有重要的意义[3~4]。
癫痫特征信号传统的提取方法是时域或频域分析,时频分析常用方法主要有短时傅里叶变换、Wigner-Ville分布、小波变换、非线性动力学分析等[5~6]。以上方法都可以对脑电信号进行简单的分析处理,但单一的方法存在实验数据识别率不高的缺点,提取效果不是很理想。现阶段小波变换和近似熵分析用的较多,但近似熵在进行复杂度计算时会产生一定的偏差,导致对细小的复杂性变化不敏感。常用的还有小波包与多元尺度熵相结合的办法[7~10]。
小波变换可以对样本信号进行多层分解,得到几组不同频率的含有特征信息的细节信号,在分析时可以舍去不含特征信息的频率段,既除去了部分噪声,又提高了特征提取的准确性。癫痫发作期间,脑电信号的波形复杂度会降低,以EEG样本熵值的大小为指标,可以体现EEG不同时期的复杂性,也可作为癫痫特征波形是否存在的依据。本研究采用小波变换和样本熵结合的癫痫信号特征提取方法。首先对获取的癫痫脑电信号进行预处理,其次对信号进行小波分解,将其分解为不同频率的子频带,小波分解后就可以看各个子频带中含有大量包括尖波、棘波等特征波形,最后对分解后的各个子频带求其样本熵值,运用熵值的大小来表示特征信号的信息。通过各个对应的子频带熵值大小的对比,可以表征癫痫特征信号的提取结果,实验熵值对比也可以用于癫痫临床的诊断。
2 算法和原理
2.1 小波分解原理
由于脑电信号是极其微弱的非平稳性信号,而且背景噪声很强。因此,如何通过量化分析提取的癫痫特征信息,是提取研究的重点。在癫痫特征信息提取分析研究中,小波变换是一种很好的时频分析方法。小波变换后信号在时域和频域的特征都可体现出来,并且还弥补了传统时域分析对信号频域和局部特征信息分析不足的缺点[11~12]。对脑电信号进行小波分解后,得到的高频部分的信号可以很好地体现信号在时间上的分辨率,低频部分的信号又具有良好的频率分辨率特征,因此小波变换对EEG进行预处理和特征提取非常适用。

连续小波变换(continuous wavelet transform,CWT)是将信号在时频上进行卷积积分,从而可以将信号分解成不同时间和不同频率上的各个子频带,也就是所需要的细节信号[13]。在处理离散信号时,需要将连续小波进行离散处理,也就是对母小波中的尺度因子a和平移参数b进行离散化处理,离散方式是将a和b转化为离散形式:
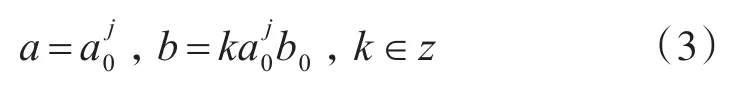
其中,a0≠1,a0是一个定值。
离散小波函数可表示为

当a0=2,b=1时,此时的离散小波就变成了常用的二进制小波(Dyadic Wavelet):

小波变换的实质就是选取出适当的小波基函数去逼近信号,也就是选取出和将要被分解的信号特征相似的一簇小波函数去分解提取出信号所包含的特征信息。癫痫发作时产生的脑电信号中包含大量的棘波和尖波等特征信号,小波变换的目的就是将特征信息分解表示出来[14~16]。在将 Matlab工具箱中的小波基函数与癫痫脑电特征波形进行对比和相关计算后,发现Daubechies波与特征波形最为近似,因此选择Daubechies小波作为分解的小波基函数。
2.2 样本熵原理
在系统的复杂性分析中,只需要少量的数据就描述整个系统的复杂程度。熵值的大小是对系统不确定性的一种度量,如果系统的熵的值越高,则表明系统越复杂,而且具有较强的随机性[17]。
通过样本熵值计算系统复杂度时,也是样本熵的值越大,系统的复杂度越高,反之,系统趋于较强的规律性和稳定性[18~19]。癫痫在发作时,EEG数据的复杂程度会明显降低,呈现出一定的规律性。因此,样本熵是一种癫痫特征提取研究的不错的方法[20]。
定义一个长度为N,数据为 x1,x2,x3,…,xN序列,其样本熵的计算原理:
1)从序列中选取出m个点作为一组向量x1,x2,…,xN-m+1,其中:
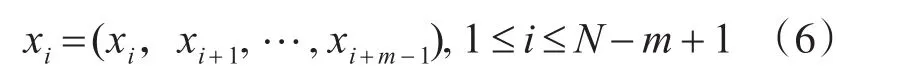
2)设向量 xi,xj之间的距离最大值为dm,则:

3)将计算过程中的设定值设为r,统计dm中数值小于r的个数,进而计算它与距离总数的比值,记为,也即是两个序列相似的概率:

由原理公式可知样本熵的大小和参数m,r的选取相关,经过实践得到通常取m=2,r=0.1—0.3*std(std表示数据的标准差)。
3 数据处理与分析
3.1 脑电信号数据采集
本研究采用的三种EEG数据是来自于采集的真实脑电数据,而且数据选取的都是进行过预处理且不包含眼心电噪声的片段,每组选取500个点作为实验数据。三种数据分别是正常脑电信号(无痫样放电EEG),发作间期(周期痫样放电EEG)和发作期(连续痫样放电EEG)的数据,三种数据的波形如图1中(a)、(b)、(c)所示。

图1 正常、发作间期、发作期的脑电信号波形
3.2 Daubechies小波分解
将采集到的无痫样放电、周期痫样放电和连续痫样放电的三种EEG数据在Matlab的算法程序下分别进行db小波4层分解,分别得到d1、d2、d3、a4,四个子频带,其波形图如图2、3、4所示。

图2 无痫样放电时的EEG小波分解
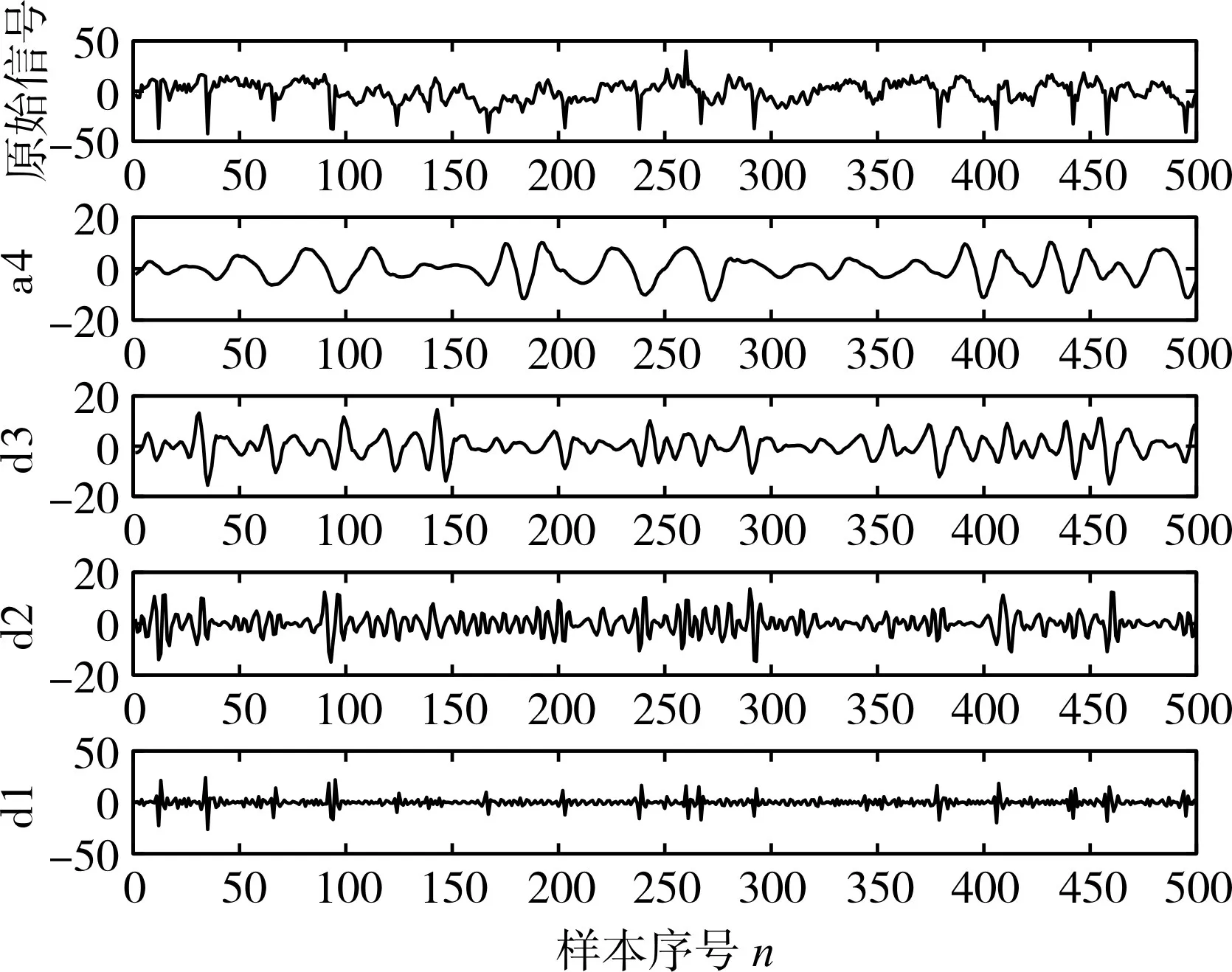
图3 周期痫样放电时的EEG小波分解
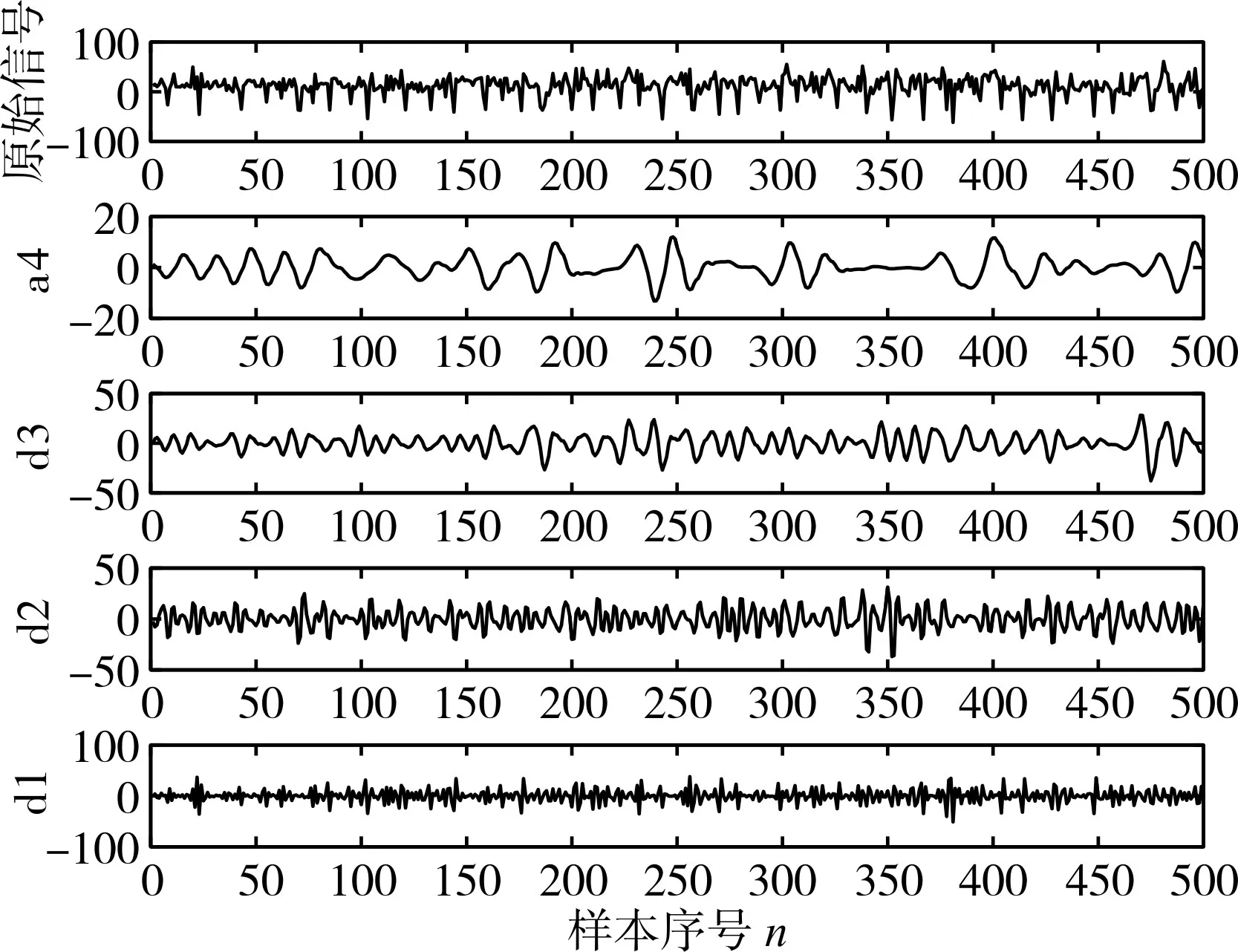
图4 连续痫样放电时的EEG小波分解
由三种数据的分解图对比所知,在发作期和发作间期EEG的数据中,子频带d1,d2,d3中包含了较多的癫痫特征信息。因此,再下一步的提取过程中,将包含有用信息的子频带单独抽取出来与正常脑电信号分解后所对应的子频带分别求样本熵,达到进一步的提取的效果。
3.3 样本熵分析
实验研究发现,在癫痫发作时脑电信号会变的具有规律性,而且复杂程度会减小,而熵的大小刚好可以反应系统的复杂程度,对图2中的三种脑电信号求样本熵,在算法程序中,参数选择m=2,r=0.15*std,得到的三者样本熵对比如图5所示。

图5 三种状态下脑电信号的样本熵
由图可知,对三种数据直接求样本熵,确实可以反映这三个时期脑电信号的复杂度,但发作期和发作间期的差别并不是特别明显,虽有一定的有效性,但在后续的检测和识别中精度不高或者无法识别。为了解决直接对三种信号求样本熵存在差别不大的缺点,本研究对分解后的各个频带的细节信号求取样本熵值,也是特征提取的第二步,在算法程序中仍选择m=2,r=0.15*std,通过对比发现正常脑电和癫痫脑电信号的熵值有明显的区分度。细节信号的样本熵如图6、7、8所示。

图6 子频带d1的样本熵对比

图7 子频带d2的样本熵对比

图8 子频带d3的样本熵对比
通过对比发现,对三种不同时期的信号分解后的子频带求取样本熵值的区分度明显比直接求取要好很多。也充分的验证了先用小波分解出子频带的必要性。样本熵对癫痫特征的提取优势在于用熵值来表示是否含有特征信息。为后续的临床检测、分类和判别过程提供了不错的实验数据。
4 结语
癫痫发作时的EEG较正常时会产生较大的形态变化,了解这些特征的变化是研究提取的基础。本文采用db4小波分解和样本熵的方法,提取癫痫特征信息。通过对来自实验室真实的脑电信号来分析,实验结果表明,在这个方法下基本可以提取出癫痫特征信息,为临床治疗提供了一些的诊断信息,也为癫痫疾病的预防和发现增加了相应的辅助手段。对后续的分类和检测工作也有很大的帮助,有进一步研究的价值。
