基于相对密度的类不平衡软件缺陷预测*
2020-08-11于化龙邹海涛
孙 丹 于化龙 郑 尚 邹海涛 王 琦
(江苏科技大学计算机学院 镇江 212003)
1 引言
软件缺陷预测[1]能够保证软件质量及其可靠性,现已成为软件工程领域的研究热点。软件缺陷预测主要通过对软件开发过程中的代码进行分析,构建准确的预测模型,并用于发现软件中潜在的缺陷。其预测结果可为测试人员进行有针对性的软件测试和维护。
一般情况下,在软件缺陷预测数据集中,无缺陷程序模块的数量要远超过有缺陷程序模块的数量,且80%的缺陷集中分布于20%的程序模块内,即软件缺陷预测训练数据集中普遍存在类不平衡问题[2]。所谓类不平衡问题,即数据集的某一类样例高于另一类,从而导致以整体错分率最小化为训练目标的分类算法失效的问题。该问题的产生会影响软件缺陷预测的结果,尤其是对少数类的预测精度降低。
目前,类不平衡问题的解决方法[3]可分为两类:一类是从调整数据集中的类分布角度出发,即采样法,包括过采样和欠采样,这类方法分别通过增加少数类样本和减少多数类样本得到分类相对平衡的新数据集[4]。另一类则从修改学习算法角度出发[·5],通过修改算法的训练过程,使得学习算法可以针对少数类有更好的预测精度。
由于软件缺陷数据集的不断增长,开发人员急需一种时间开销小,预测性能高的预测模型。极限学习机(Extreme Learning Machine,ELM)[6]具有泛化能力强、训练速度快的优点[7~8],但其也存在缺点,即当数据分布极为不平衡,分类性能往往大幅下降。Zong等[9]借鉴代价敏感学习[10]的思想,提出了一种加权极限学习机(Weighted Extreme Learning Machine,WELM)算法,有效降低了少数类被错分的概率。
尽管WELM算法能在一定程度上提升ELM在类不平衡数据上的分类性能,但仅根据类不平衡比率为每类样本分配一个统一的权重,并没有考虑样例在特征空间中的具体分布情况。因此,为了解决上述问题,本文提出了一种基于相对密度方法的模糊加权极限学习机-FWELM-RD算法,该方法通过K近邻概率密度估计法-KNN-PDE[11]来计算各训练样本间的类间相对密度,即通过精确计算任意不同类训练样本之间的概率密度比例关系来避免概率密度的测量。相对密度与数据在特征空间中的分布比无关,具有较强的鲁棒性。并引入模糊集的概念,设计相应隶属函数,从而提出用于类不平衡软件缺陷预测的模糊加权学习机算法。通过在软件缺陷数据集上的实验验证,该方法和传统的处理软件缺陷类不平衡问题方法相比,具有更好的预测性能,并且在 G-mean[12]、AUC[13]和 Balance[14]等评价指标上有较好表现。
2 基础理论
2.1 极限学习机
2006年,Huang等[6]针对单隐层前馈神经网络的训练问题,提出了极限学习机的理论与算法。极限学习机不需要对网络的权重和偏置进行迭代调整,而是通过随机指定隐藏层参数,利用最小二乘法产生唯一的最优解,因而极大地提升了训练速度,同时在一定程度上降低了陷入过拟合的概率。
假设训练样本集包括N个训练样本,将其表示为(xi,ti)∈Rn×Rm,其中,xi表示n×1维的输入向量,ti表示第i个训练样本的期望输出向量,在分类问题中,n代表训练样本的属性数,m代表样本的类别数。若一个具有L个隐层节点的单隐层前馈神经网络能以零误差拟合上述N个训练样本,则意味着存在 βi,ai及bi,使得下式成立:
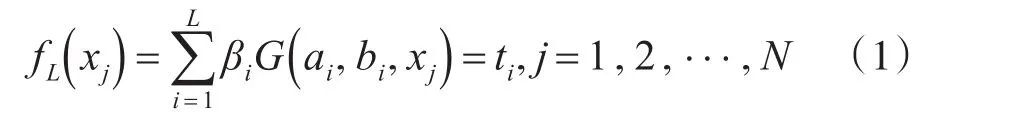
其中,ai和bi分别表示第i个隐层节点的权重与偏置;βi表示第i个隐层节点的输出权重;G表示激活函数。则式(1)可进一步简化为下式:

2012年,Huang等[15]对ELM进行了改进,增加了惩罚因子C来调节算法的泛化性和准确度,改进后的优化式如下:
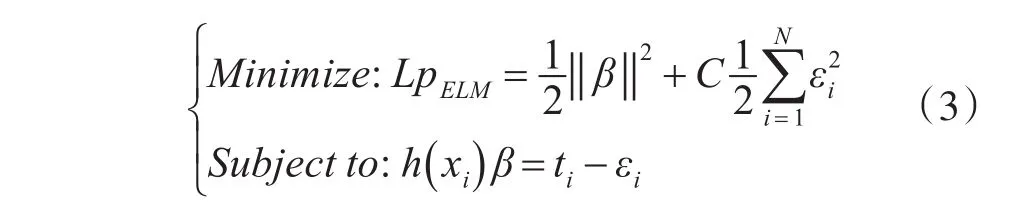
其中,εi表示第i个训练样本的实际输出与期望输出之差,h(xi)为第i个样例xi在隐层的输出向量,C为惩罚因子,用于调控网络的泛化性与精确性间的平衡,根据 Karush-Kuhn-Tucker(KTT)理论[16],上述优化式(3)可通过下式求得:
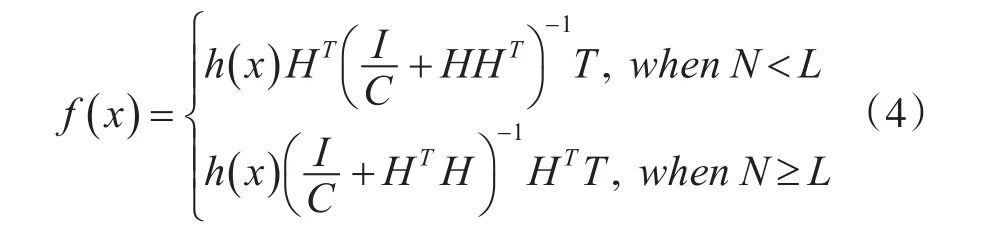
2.2 加权极限学习机
ELM在处理软件缺陷类不平衡问题时,也面临着和传统分类器同样的问题,即分类性能大幅度下降,大量的少数类被误分为多数类。针对这种问题,Zong等[9]提出了WELM算法,该算法在式(3)的基础上增加了一个加权矩阵,以此为不同类样本赋予不同的权值,从而更好地反映出不同样本在不同类中的重要性,获得比ELM更好的泛化性能。其中,W为一个N×N的对角阵,它为各类样本分配权值;Wii为第i个训练样例的权值。Zong等提供了如下两种权值分配方法:
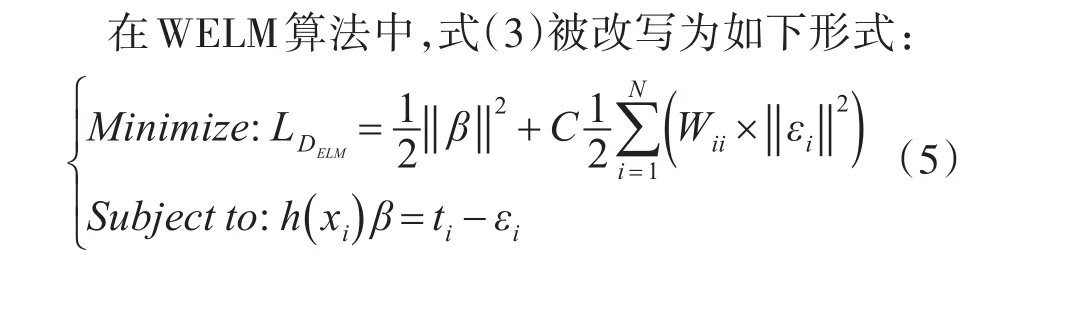
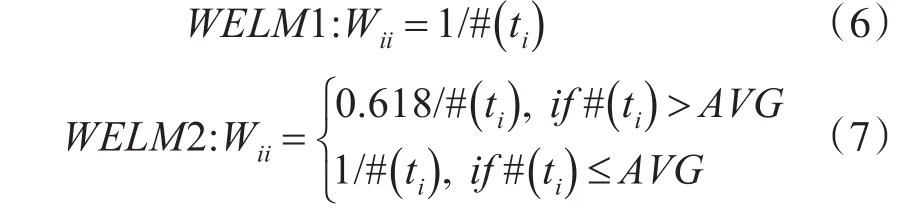
根据KKT定理,得到关于β的解:
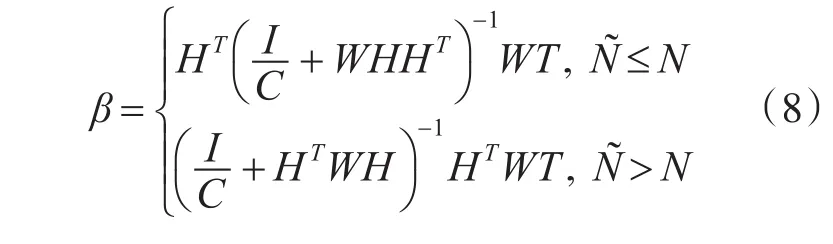
3 本文方法
3.1 相对密度的计算
加权极限学习机的权值矩阵并不具有对软件缺陷数据样本信息的判别能力,即对同一类别中的噪声样本和非噪声样本所分配的权值是一样的。因此,为了解决上述问题,得到分类性能更好的WELM算法,本文结合相对密度,引入模糊集并设计隶属函数,提出基于相对密度的模糊加权极限学习机算法。
首先,若能精确地测出每一个训练样本的概率密度,从噪声点和离群点中区分出具有重要信息的样本则变得比较容易。但是,在高维特征空间中,获得精确的概率密度是极为困难的,要获取相对精确的概率密度也是十分耗时的。因此,本文采用了一种避免概率密度测量的方法,即精确计算任意两个训练样本之间的概率密度的比例关系。这种反映比例关系的信息称之为相对密度。为了获取这种相对密度,本文采用类KNN-PDE方法[11]。作为一种无参概率密度估计法,KNN-PDE通过计算每个训练样本的K近邻距离来评估多维特征空间的概率密度分布。当训练样本的数目无穷大时,KNN-PDE方法所获得的结果更接近于真实的概率密度分布。
假设一个数据集有N个样本,对于每个样例xi,找到它的K个最近的样本并计算它们之间的距离。众所周知,越大,样本xi的密度就越高。同样地,对于那些出现在低密度区域的噪声点和离群点,也可用来衡量每个样本的重要程度。但是,为了分别增加和降低高密度样本和低密度样本(即噪声和离群点)的影响,一般取的倒数,并将样本的K近邻距离的倒数称之为相对密度。不难看出,任意两个样本之间的相对密度和它们之间K近邻距离的比例关系成反比,即:
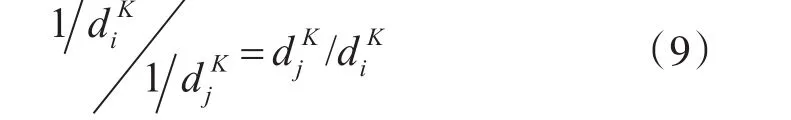
若K值太小,则很难将噪声点和离群点从普通样本中区分出来;若K值太大,则那些重要样本与噪声点或离群点之间的区别便会变得模糊不清而这些微小的差距将更难获取。
3.2 隶属函数的设计
对于一个模糊加权算法而言,影响其性能的最关键因素即是隶属函数设计的合理性,故针对类不平衡问题,本文在相对密度概念的基础上,设计了一种隶属函数[17],该函数采用类间密度信息来计算。在该方法中,定义该隶属函数为,该函数和预估类边界相关,即接近预估类边界的样本会被赋予一个较大的值。为了更准确地估量类边界,本文深入研究了关于不同密度分布的四种样本的特征。这些样本被分为四种类型,分别为正常样本、边界样本、噪声样本和离群样本。图3展示了这些样本直观描述。这四种样本的特征总结如下。
1)正常样本:该类样本出现在自身类样本的高密度区域,其他类样本的低密度区域。
2)边界样本:该类样本出现在两类样本的低密度或中间密度区域,但相比其他类样本,其在自身类样本密度要高一些。
3)噪声样本:该类样本出现在自身类样本的低密度区域,其他类样本的高密度区域。
4)离群样本:该类样本出现在两类样本的低密度区域。

图1 四种不同样本示例图
根据上述描述,我们可以准确地确定边界。首先,对于每个样本,可以通过比较其类内和类间的相对密度来寻找噪声样本,且可以根据一个判别式来寻找。若样本是正类样本,则它的判别式如下:
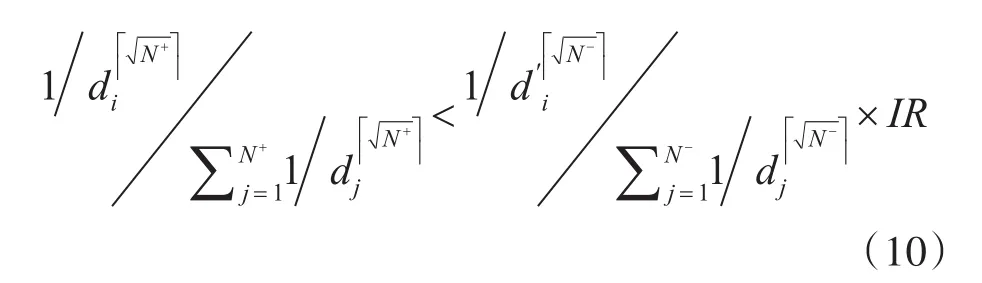
其中,d′表示该类和另类的距离计算而得,N+和N-分别为正类和负类样本的个数。为为聚集操作,IR为类不平衡比率N-N+。若样本xi是负类样本,则它的判别式如下:
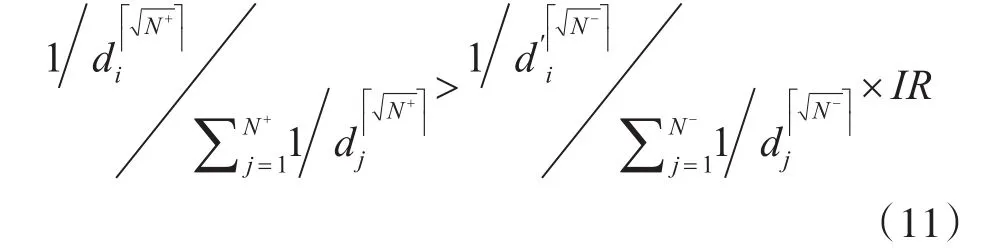
对于每个满足判别式(10)和式(11)的样本,将被作为噪声样本去除,并给它们赋予一个很小的函数值l。
对于剩下的样本,根据类间相对密度对其分配函数值。模糊隶属函数值可用分段函数表示:
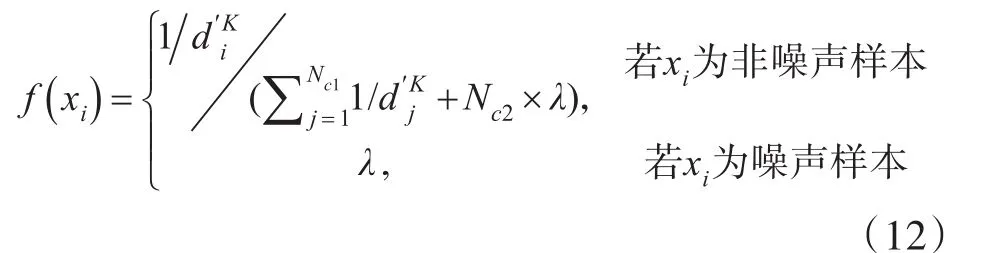
其中,为Nc1和Nc2分别表示在同一类下的xi属于非噪声样本和噪声样本的数目,且有Nc1+Nc2=Nc。
3.3 基于相对密度的模糊加权极限学习机
上述过程给出了类间相对密度及隶属函数的求解过程,为了提升加权极限学习机的预测性能,将隶属函数值作为每个训练样本的权值,转换成对角阵,并将其替换WELM中的Wii对角阵,完成相对密度方法和加权极限学习机的结合,即基于相对密度的模糊加权极限学习机算法(FWELM-RD)。下面给出该算法步骤:

步骤1将Θ分成两个数据集,Θ+只包含正类样本,Θ-只包含负类样本;
步骤2计算Θ+和Θ-的样本数,并分别记为 N+和N-,且 N++N-=N ;
步骤3计算类不平衡比率IR=NN+;
步骤4分别计算正负类样本的参数K,记为K+=
步骤5对于Θ+里的每个样本xi+,计算它在Θ+里的K+近邻距离及在Θ-里的K-近邻距离,在分别并记为di+和di-,同样地,对于Θ-里的每个样本xi-,计算它在Θ-里的K-近邻距离及它在Θ+里的K+近邻距离,并分别记为dj-和dj+;
步骤6计算每个样本的相对密度并分别通过式(10)和式(11)找出两种不同类内的噪声样本;
步骤7对于每个样本xi,通过式(12)计算其隶属函数值Si;
步骤8将隶属函数值 f()xi嵌入到WELM的加权矩阵Wii中;
步骤9用惩罚因子C,隐藏层神经元数L训练WELM,获得新的权值矩阵Wii′。
4 实验分析
本文在极限学习机的基础之上,提出类不平衡软件缺陷预测算法,从而得到分类精度更高、泛化能力更好的模型。所提模型将采用10折交叉验证,即每次将数据集分成10份,轮流将其中9份作为训练集并建立模型,1份作为测试集进行验证,整个过程将重复100次,最后取其结果的均值作为各种指标值,整个方法框架如图1所示。
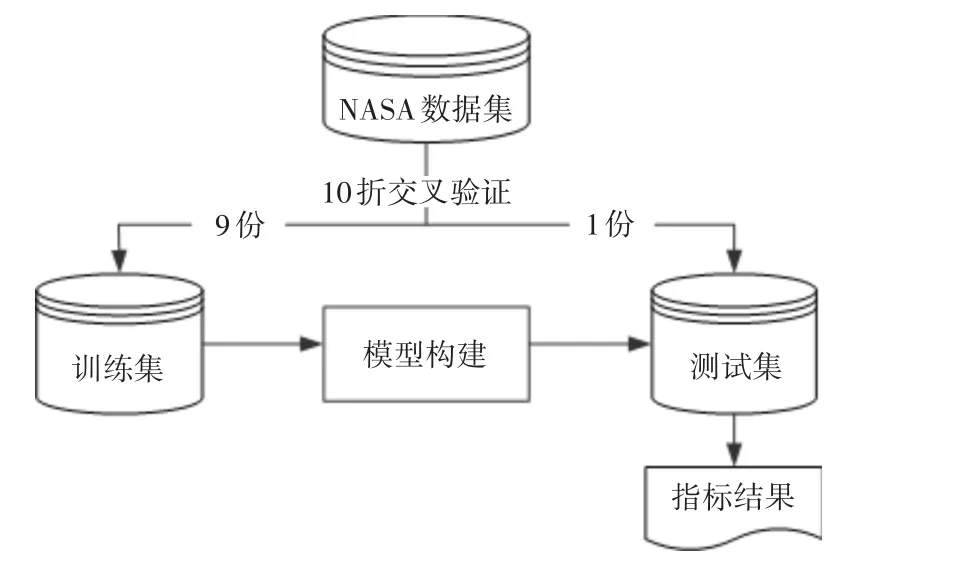
图2 方法框架
为了验证所提方法,本文从PROMISE数据库中选取了10个NASA软件缺陷预测数据集[18],并与传统的软件缺陷预测方法进行实验分析对比。
4.1 数据集与参数设置
本 文 的 实 验 环 境 为 Intel(R)Core(TM)i5-3230M,CPU主频2.6 GHz,内存8 GB;操作系统为Windows 10;编程环境为Matlab2014a。
实验所用数据集为美国国家航空航天局(NASA)发布的专门用于构建软件缺陷预测模型的公开数据集,度量属性包括Halstead属性、McCabe属性、代码行数等属性。所用数据集的基本信息如表1所示,其中数据集按缺陷率排序。
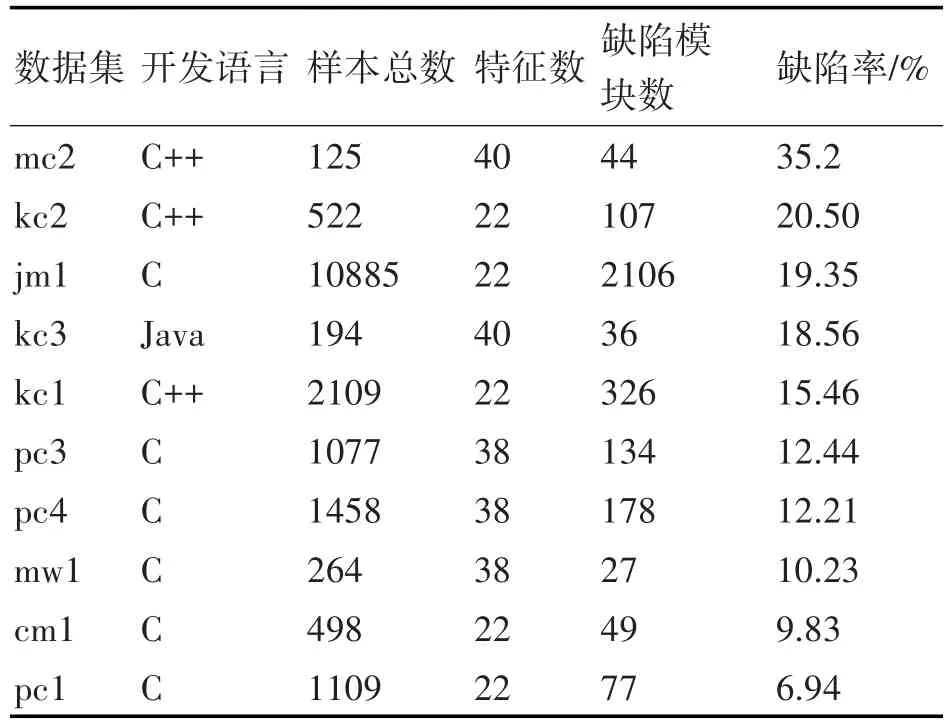
表1 实验数据的基本信息
本文将与具有代表性的DNC(Dynamic Ada-Boost.NC)集成学习方法[19]进行对比验证。同时,为了验证基准方法ELM的有效性,本文还与ELM[6]、ELM-RUS[5]、ELM-ROS[20]、ELM-SMOTE[21]、
WELM1[9]和 WELM2[9]算法进行比较,以上方法可根据前人文献所提供代码流程实现,并同样采取10折交叉验证方法保证结果一致性。
在实验中,本文对所有ELM算法设置了统一参数,以此来保证实验对比结果的公正性,即对于ELM中的隐藏层节点数L和惩罚因子C,均给定了相同的取值范围,其中,L∈{ }10,20,…,300 ,C∈{2-4,2-2,…,220},实验中采用了Grid Search策略得到了最优的参数组合—L为100,C为212。
4.2 评估标准
考虑到软件缺陷预测数据集的类不平衡分布问题以及软件系统的不同需求性,本文采用了多个评估标准来衡量预测模型的性能。所用评价指标常用的G-mean[12]指标外,还采用了AUC值和Balance值作为评价指标。在人工智能中,混淆矩阵是表示精度评价的一种标准格式,用n行n列的矩阵形式来表示。本文所用混淆矩阵如表2所示,并定义预测率(Probability of Detection,PD)定义为PD=TP/(TP+FN);误报率(Probability of False Alarm,PF)定义为PF=FP/(FP+TN)。有G-mean定义为
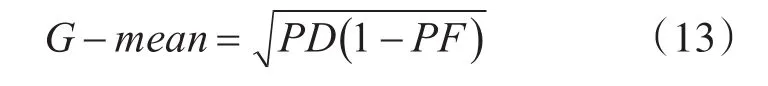
其中TP指被model预测为正的正样本,TN指被model预测为负的负样本,FP指被model模型预测为正的负样本,FN指被模型预测为负的正样本。
AUC(Area Under Roc Curve)是评估模型准确率的一种方法,可通过对ROC曲线下各部分的面积求和而得。模型的准确率越高,面积越接近1。随机预测的面积为0.5,而完美模型的面积为1。AUC值越大,则预测模型的性能越好。
考虑到点(PF=0,PD=1)是ROC曲线中最理想的点,在(0,1)点所有的错误都能被正确识别出,所以软件工程师经常在实践中用到一种权衡PD和PF的综合指标Balance,该指标计算真实的(PF,PD)点到(0,1)的欧式距离,其定义如下:

由上式可知,Balance值越大,表示(PF,PD)点与(0,1)之间的距离越近,分类性能越好,反之则越差。
4.3 实验结果与讨论
表3~5分别列出了由8种方法构造的软件缺陷预测模型在10个NASA数据集上的3种指标(G-mean、AUC和Balance)的平均值。

表2 混淆矩阵
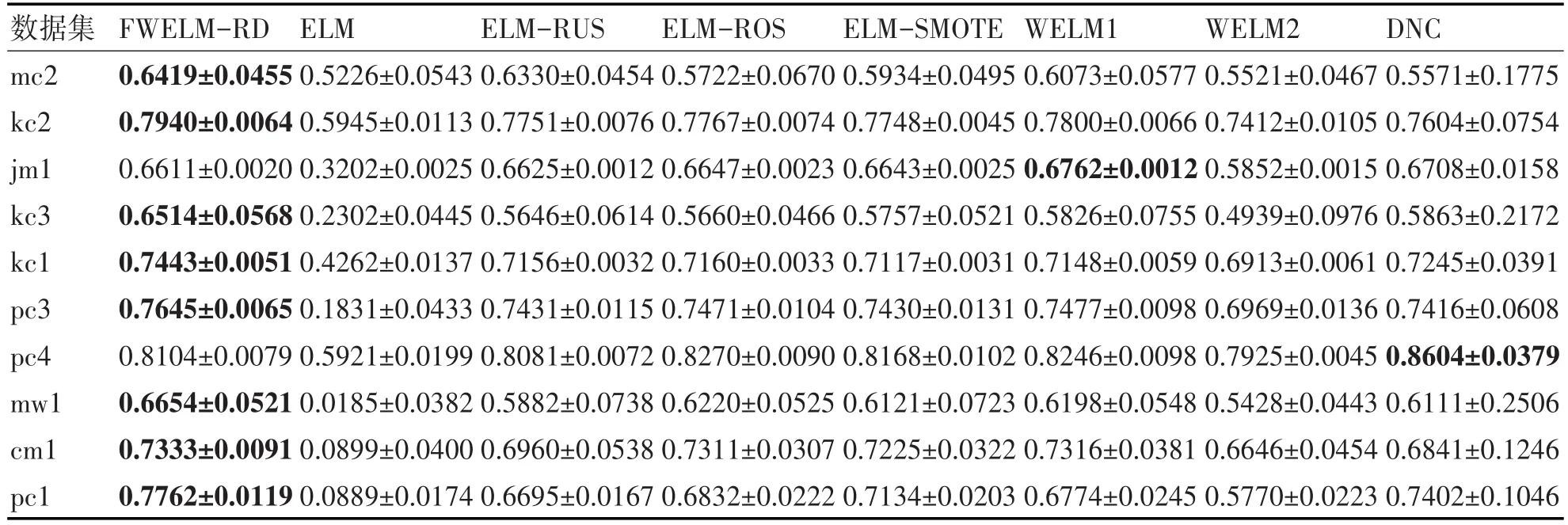
表3 各类算法的G-mean测度比较
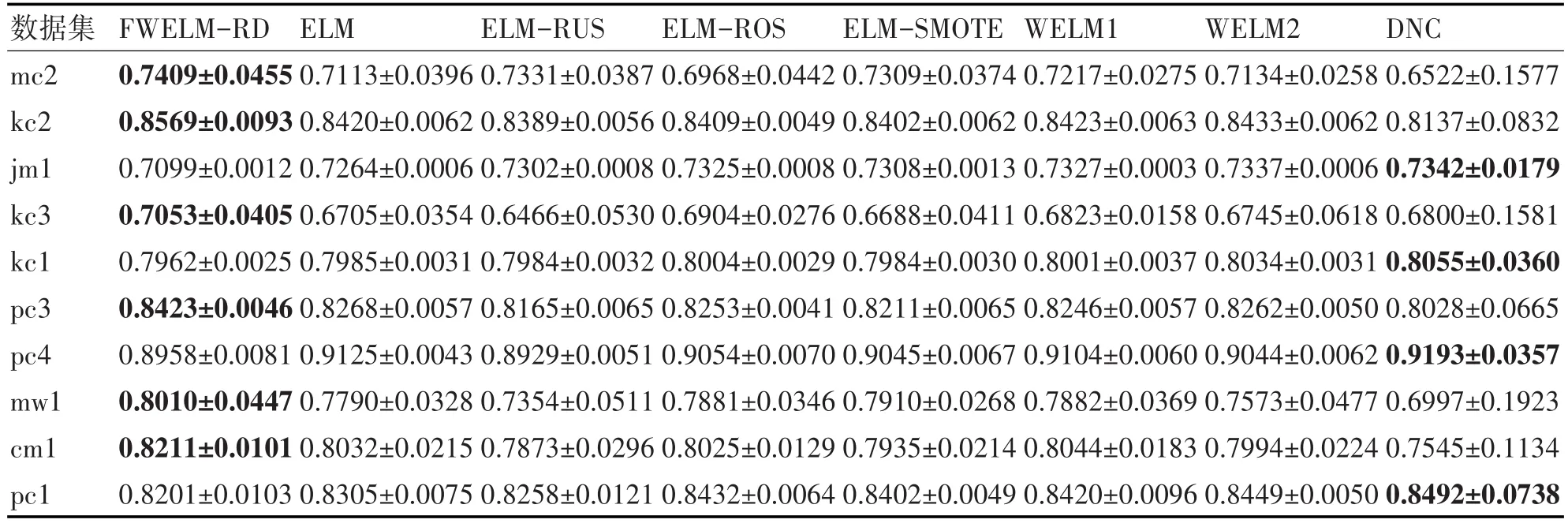
表4 各类算法的AUC测度比较
根据表3的G-mean描述,本文所提算法较其他基于ELM的类不平衡学习算法及两种WELM算法都有很大的提高,同时也大部分优于基于集成学习的DNC方法。由表4的AUC结果得知,本文所提算法与其他方法相比皆有相当性能。针对软件工程师常用的Balance指标,根据表5的结果可知,本文所提FWELM-RD方法在大部分数据集有着较优的性能。
此外,本文对各个算法的性能进行了统计分析。Friedman检验[22]是利用秩序实现对多个总体分布是否存在显著差异的非参数检验方法,其原假设是:来自多个配对样本的多个总体分布无显著差异。通过计算Friedman统计量和对应的概率P(adjusted p-value,APV)值,来判断其是否拒绝原假设。若APV值小于给定的显著性水平α,则拒绝原假设,认为各组样本的秩存在显著差异,来自多个配对样本的多个总体的分布有显著差异;反之,则不能拒绝原假设,可认为各组样本的秩不存在显著性差异。
本文用Friedman检验来对各算法在所有数据集上的性能按G-mean、AUC和Balance分别计算它们的秩及APV值,其中,显著性水平α设为0.05。统计分析结果如表6所示。其中,G-mean、AUC和Balance性能指标的平均秩和APV值分别用rankingG 、rankingA、rankingB和APVG、APVA、APVB表示。
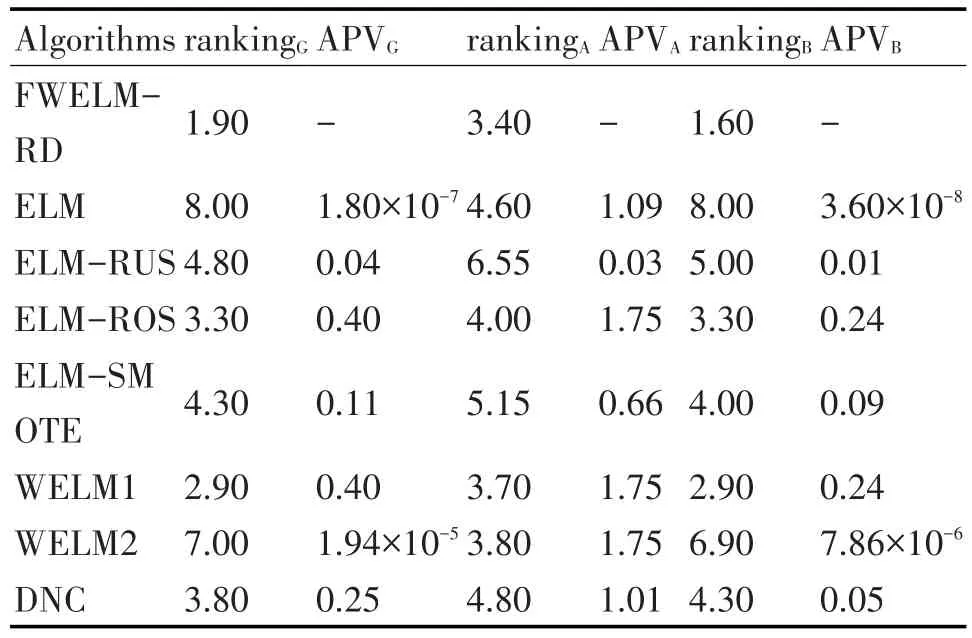
表6 不同算法的统计结果
算法性能最好的ranking值最小,排序为1,算法性能其次的ranking值第二小,排序为2,并以此类推。从表6可以看出,FWELM-RD算法在三项指标里的ranking值均最小,即排名均为1,这表明该算法在所有算法中具有最好的预测性能。
5 结语
本文以软件缺陷预测为背景,针对类不平衡对预测模型的性能产生的影响,提出了一种基于相对密度的模糊加权极限学习机算法。该算法在原有加权极限学习机算法的基础上,引入模糊集的思想,通过隶属函数的设计,对每个样本的权重进行模糊化与个性化的设置,从而缓解类不平衡对软件缺陷预测性能的影响,以达到提高预测模型性能的目的。选取了公开的NASA数据集进行实验。结果表明,所提算法构造的预测模型具有更好的预测性能,从而帮助软件缺陷预测工作更好地进行。
此外,在下一步的研究工作中,希望在以下方面进行拓展:
1)对于相对密度计算方法中涉及的参数K的选取,若选取其他更多值,结果是否有影响,还需进一步实验验证;
2)对更多的算法进行实验比较,更进一步来验证本文算法的有效性;
3)选取更多的软件缺陷数据进行验证所提算法。
