抓住核心知识 感悟统计思想

孙伟刚

“数据的收集、整理与描述”的主要学习内容为：①利用全面调查或抽样调查（以抽样调查为重点）收集数据;②利用科学合理的表格整理数据;③利用统计图（以直方图为重点）描述数据;④展现收集、整理、描述和分析数据得出结论的统计调查的基本过程等.为了帮助同学们更好地巩固与提升这部分内容，现撷取核心知识予以解析，

一：全面调查与抽样调查

例1 （2019年抚顺）下列调查中，最适合采用全面调查的是（）.

A.对全国中学生视力和用眼卫生情况的调查

B.对某班学生的身高情况的调查

C.对某鞋厂生产的鞋底能承受的弯折次数的调查

D.对某池塘中现有鱼的数量的調查

解析：A选项中，全国中学生人数众多，应当采用抽样调查，故此选项错误;B选项中，一个班学生人数少，范围小，应当采用全面调查的方式，故此选项正确;C选项中，调查鞋底能承受的弯折次数，由于破坏性较强，适宜采用抽样调查，故此选项错误;D选项中，调查某池塘中现有鱼的数量，调查难度大，适宜采用抽样调查，故此选项错误，故选B.

点评：本题考查了抽样调查和全面调查的区别，选择全面调查还是抽样调查要根据所要考察对象的特征灵活选用.一般来说，当调查具有破坏性、全面调查无法进行或者全面调查的意义或价值不大时，应选择抽样调查：对于精确度要求高的调查，事关重大的调查或者所费人力、物力和时间较少的调查往往选用全面调查.

二、总体、个体、样本和样本容量

例2某市有7.6万名学生参加初中毕业会考.为了解这7.6万名学生的数学成绩，从中抽取1 000名学生的数学成绩进行统计分析.以下说法正确的是（）.

A.这1000名学生是总体的一个样本

B.7.6万名学生是总体

C.每名学生的数学成绩是个体

D.1 000名学生是样本容量

解析：8A选项和B选项中，没有明确具体对象的数量指标，我们要研究的不是这些对象本身，而是其某种指标，故这两个选项错误：C选项中，明确了考察对象的“数学成绩”这一数量指标，符合个体的概念，故此选项正确：D选项中，样本容量是指抽取的样本中所包含的个体数目，即1 000，而非1 000名学生，故此选项错误.故选C.

点评：本题考查了样本的概念，同时也考查了对总体、个体、样本容量的概念的理解.我们把所要考察对象的全体叫作总体，把组成总体的每一个考察对象叫作个体，从总体中取出的一部分个体叫作这个总体的一个样本，一个样本包括的个体数目叫作样本容量，只有正确理解这些概念，才能分清具体调查中的总体、个体与样本.解决这类问题的关键是明确考察对象.总体、个体与样本的考察对象是相同的，所不同的是范围的大小.

三、统计图表的补制及信息转换

例3（2019年泰安）为弘扬泰山文化，某校举办了“泰山诗文大赛”活动，并从中随机抽取部分学生的比赛成绩，根据成绩（成绩都高于50分）绘制了表1和图1（均不完整）.

请根据以上信息解答下列问题.

（1）求a，b的值.

（2）计算扇形统计图中“第5组”对应扇形圆心角的大小.

（3）若该校共有1 800名学生，则成绩高于80分的有多少人？

解析：（1）根据表中的信息可知，第3组人数为10，同时根据扇形统计图中的信息可知，第3组人数占25%，这样可求得抽取的学生总人数为10÷25%=40.而第2组人数占30%，于是第2组人数为a=40x30%=12.第4组人数为6 =40-8-12-10-3=7.当然求6的值还可以这样做：先求出第1组人数和第5组人数分别占20%和7.5%，然后求出第4组人数占1 -20%一30%一25%一7.5%=17.5%，故b=40x17.5%=7.

（2）由于第5组人数占3÷40x1 00%=7.5%，故“第5组”对应扇形圆心角的大小为3600x7. 5%=270.

（3）由表l可知成绩高于80分的组是第1组和第2组，同时观察扇形统计图，发现第1组人数和第2组人数共占20%+30%=50%.因此所求人数大约为1 800x50%=900.

点评：本题考查的是表格和扇形统计图的综合运用.读懂表格与统计图，从图表中得到必要的信息是解决问题的关键.本题先以残缺的图表以及文字表述提供数据信息，然后通过填补使得图表完善，但最后落脚点在统计图表的信息转换上，问题（1）为问题（2）、问题（3）做了充分的信息准备，实际上是一道融图表于一体，并补全图表信息的综合题.

练一练

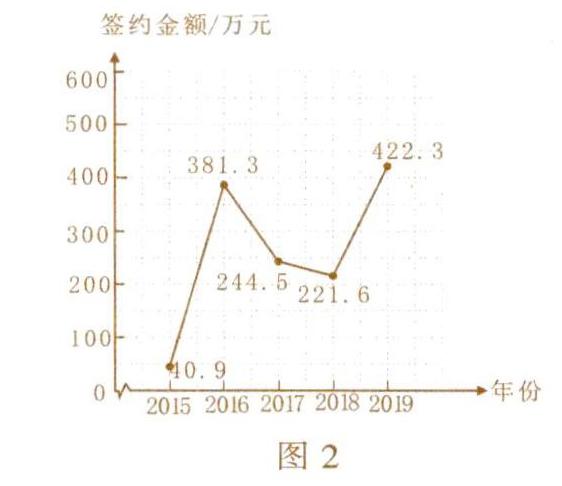
（2019年舟山）2019年5月26日，中国国际大数据产业博览会召开，某市在历届产业博览会上的签约金额的折线统计图如图2所示，下列说法正确的是（）.

A.签约金额逐年增加

B.与上年相比.2019年签约金额的增长量最多

C.签约金额年增长速度最快的是2016年

D.2018年签约金额比2017年降低了22.98%

参考答案：C