深厚淤泥中双排钢板桩结构安全稳定性研究
2020-08-10郑国兵黄朝煊袁文喜吴留伟徐轶慷
郑国兵,黄朝煊,袁文喜,吴留伟,吴 蕾,徐轶慷
(浙江省水利水电勘测设计院,浙江 杭州 310002)
钢板桩于20世纪初应用于欧洲,之后在欧洲和日本取得了长足的发展,目前在国内广泛应用于船坞、码头、桥梁、水闸、泵站等领域的施工围堰和基坑支护。钢板桩施工方便,有助于降低工期,同时其结构安全可靠、占地空间小,在水利、交通、市政和港航等工程中得到推广应用。
由于双排钢板桩较单排钢板桩而言具有整体刚度更大、安全稳定更可靠、无需设支撑、占地面积小等优点,因此双排钢板桩围堰在软土地基和深厚覆盖层地基中应用广泛,但在滨海淤泥地基中应用较少,其工程实践经验也较欠缺,特别是在宽阔海域的围垦工程淤泥地基中应用经验更少。
江杰等[1-2]分别基于冗余度和可靠度对双排钢板桩围堰稳定进行了分析探讨,张玉成等[3]利用有限元对典型围堰支护结构进行了计算分析,吴留伟等[4]对双排钢板桩围堰设计进行了总结分析,黄朝煊[5]对双排长短桩框架海堤结构进行探讨,董志良等[6]对大面积围海造陆围堰工程相关技术进行分析探讨,朱旋等[7]通过有限元软件对双排钢板桩围堰进行了有限元计算探讨,但以上研究均未对板桩入土深度等关键设计参数的作深入研究。本文依托浙江省某大型围垦工程,对宽阔海域的深厚淤泥地基中双排钢板桩围堰入土深度等设计及施工关键技术进行总结提炼,以期为类似工程设计施工提供参考。
1 双排钢板桩计算模型分析
对于宽阔海域内深厚淤泥地基中的双排钢板桩结构,其地基土孔隙比大、含水量高、可压缩性大且承载力差,同时受外海潮位影响及波浪荷载的作用,受力复杂,因此本文采用图1所示简化模型计算(图中Ld为双排钢板桩入土深度;H为钢板桩顶至涂面之间高差;hs为换填砂厚度;h为双排钢板桩内外侧抛石镇压层厚度;B为双排钢板桩结构的排距,γm1、cm1、φm1分别为第一层地基土的容重、黏聚力和内摩擦角;γm2、cm2、φm2分别为钢板桩持力层地基土的容重、黏聚力和内摩擦角)。

图1 双排钢板桩计算模型示意图
1.1 钢板桩刚度安全性控制
依据文献[8],抗剪切变形稳定安全系数按下式计算:
(1)
式中:Mf为钢板桩结构所能提供的极限抵抗力矩;Ms为钢板桩所受的变形力矩,指海底面以上的墙前波浪力、墙后土压力、桩间剩余水压力以及上部结构所受的外荷载对海底面的力矩;Kv为抗剪切变形安全系数,取1.2。
1.2 钢板桩排距及入土深度安全性控制
依据标准[9],双排钢板桩底部抗隆稳定安全计算公式为
(2)
其中Nq=tan2(45°+φm2/2)exp(πtanφm2)
Nc=(Nq-1)/tanφm2
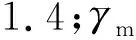
双排钢板桩结构在满足抗隆安全稳定条件下,可以将双排钢板桩及其内部回填料整体等效为“重力式结构”,因此其整体重力式结构需满足整体抗滑移稳定和整体抗倾覆稳定性计算要求。
整体滑移稳定安全计算公式为[9]

(3)

式中:Ks1为抗滑安全系数,其值不应小于1.2;Eak、Epk分别为等效重力式结构上的主动土压力、被动土压力值;σakj、σpkj分别为双排钢板桩的基坑内侧、外侧计算点的第j层土中竖向应力值;cmj、φmj分别为第j层土的黏聚力和内摩擦角;G为等效重力式结构的自重;um为等效重力式结构底面上的水压力,位于含水层时,可取um=γw(hwa+hwp)/2;hwp、hwa分别为等效重力式结构内外侧的压力水头;B为等效重力式结构的底面宽度;Fw为立波作用下的浪压力,其计算方法参考JTS 154-1—2011《防波堤设计与施工规范》[10]。
抗倾覆稳定性计算公式为[9]

(4)
式中:Kov为抗倾覆安全系数,其值不应小于1.3;aa为等效重力式结构外侧主动土压力合理作用点至底趾的竖向距离;ap为等效重力式结构内侧被动土压力合理作用点至底趾的竖向距离;aG为等效重力式结构自重与底部水压力合力作用点至底趾的竖向距离;aw为立波作用下的浪压力合力作用点与涂面之间的距离。
双排钢板桩整体滑动稳定计算,依据规范,在瑞典条分法且等步长条分土条时,采用总应力法计算:

(5)
式中:Ks为整体滑动稳定安全系数;Wi为土条i的重量;bi为第i个土条的宽度;cmi为土条i滑动面上土体的黏聚力;φmi为土条i滑动面上的内摩擦角;αi为土条i滑动面中点的切线与水平线的夹角。
值得说明的是双排钢板桩围堰结构整体滑动稳定需考虑侧向“拉拽”及整体“空间效应”的影响。
1.3 其他安全辅助加固处理措施
对表层淤泥层采用砂换填后,既有利于下部淤泥土的竖向排水固结[11],增强下部淤泥土的抗剪强度,同时在地基土面层形成“硬壳层”,对双排钢板桩整体结构稳定具有较大的有利影响。
换填砂厚度hs根据下卧层地基承载力确定[12]:
γh+γshs≤fa
(6)
其中fa=Mbγb+Mdγd+Mcck
式中:K0为土层的静止土压力系数,K0=1-sinφm1;γ为抛石镇压层的容重;γs为换填砂的有效容重;b为双排桩的宽度;d为置换厚度;ck为置换层原状土的黏聚力。
2 最小入土深度计算计算公式
2.1 抗隆稳定条件
根据式(2),求解关于Ld的方程,得满足抗隆稳定下的钢板桩的入土深度应满足:
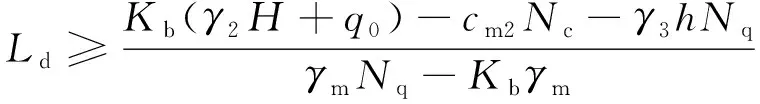
(7)
2.2 整体抗滑移稳定条件
根据式(3),通过数学理论推导得:
A2Ld2+A1Ld+A0≥0
(8)

A0=(cm2-umtanφm2)B+γ2Htanφm2-
根据工程实际经验,一般可取B=H,求解一元二次不等式(8)可得:
(9)
2.3 抗倾稳定条件
根据式(4),通过数学理论推导得:
(10)
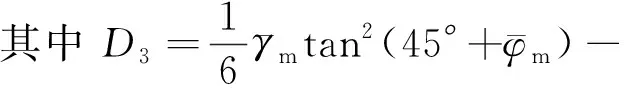
由一元三次方程的卡当公式解,求解以上方程可得满足抗倾覆稳定下的入土深度应满足:

(11)

2.4 满足稳定条件的最小入土深度
双排钢板桩结构入土深度Ld设计初值可取分别满足抗隆稳定、整体抗滑移稳定和抗倾稳定计算值中的最大值,即:
(12)
值得说明的是,对于受外海潮位及波浪压力作用下的双排钢板桩结构,由于水压力作用下弯矩的不利影响更大,因此水压力对整体抗倾覆的影响比整体抗滑移的影响更显著,此时按整体抗倾覆稳定计算得出的入土桩长临界值比按整体抗滑移稳定得出的临界值更大。
3 工程案例
3.1 工程概况
浙江省某大型围垦工程[13]位于温州市瓯江、飞云江两河口之间,总围垦面积8 853 hm2,主要包括海堤、水闸及通航建筑物,工程等别为Ⅰ等,海堤、水闸等主要建筑物级别为1级。北闸位于围垦区北部,水闸规模为10孔×8 m+6孔×8 m+通航孔16 m。在基坑外侧布置环形围堰,通过环形围堰,在海上形成一定的造陆区域,为后期水闸地基处理和旱地施工创造条件。
围堰施工区内分布深度超过30 m的淤泥土,具有饱和、流塑和高压缩性等特点,地基土层结构主要有:①流泥,层厚为0.30~0.50 m;②Ⅲ0层淤泥,层厚为2.00~2.50 m;③Ⅲ1层淤泥夹粉砂、粉土层,层厚为5.00~6.50 m;④Ⅲ2层淤泥,层厚为14.00~16.00 m;⑤Ⅲ3层淤泥,层厚3.00~5.00 m;⑥Ⅳ1层淤泥质黏土,层厚3.00~7.00 m。各土层主要物理力学特性指标表见表1。
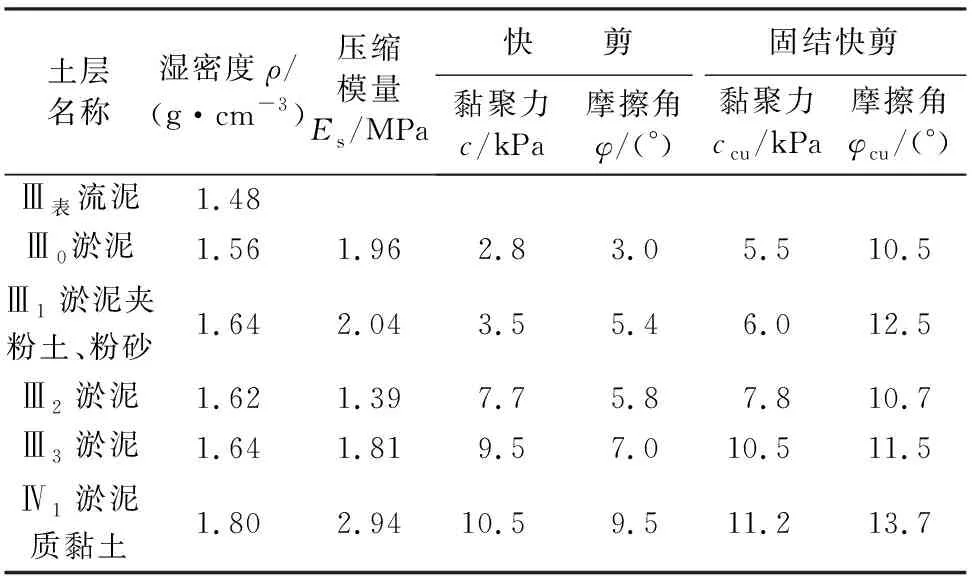
表1 土层主要物理力学特性指标
围堰整体环形布置,设计轴线总长1 533 m,围堰内基坑面积14.5万m2,围堰平面布置见图2。围堰两端布置两个60 m长的刚性复合地基(∅80 cm的PHC桩)抛石围堰段(人工岛),其余段采用双排钢板桩围堰。双排钢板桩围堰段两排钢板桩之间设置44道横隔钢板桩,横隔布置间距约为35 m,将内外两排钢板桩分割成44个隔仓,以提高双排钢板桩整体刚度。围堰顶宽11.00 m,设计顶高程5.50 m(以基坑侧钢板桩顶高程计),内外侧设置抛石镇压平台,内外侧镇压平台高程-0.50 m。钢板桩采用U型冷弯钢板桩,单根长27 m,截面模量3 200 cm3/m。拉杆采用∅70 mm钢拉杆,间距1.4 m。围堰典型断面见图3。其中钢板桩施工打设现场图见图4。

图2 水闸围堰实景鸟瞰图

图3 水闸围堰典型断面(单位:m)

图4 钢板桩围堰施工图
3.2 基于本文计算公式的分析
由式(7)计算得Ld≥15.16 m;由式(9)计算得Ld≥8.63 m;由式(11)计算得Ld≥17.01 m。最后依据式(12),双排钢板桩在满足抗隆、整体抗滑移以及抗倾覆稳定条件下的入土桩长最小值满足Ld≥17.01 m。
本工程中双排钢板桩实际设计桩长为18.5 m,比理论计算值稍偏大。
双排钢板桩围堰整体滑动稳定计算采用瑞典条分法,依据《浙江省海塘工程技术规定》进行验算,通过试算求得圆弧半径37.57 m,安全系数KS=1.21> 1.20,满足整体滑动稳定要求。
值得说明的是,计算中未考虑换填砂对淤泥质地基土排水固结而提高抗剪强度的有利影响,同时在双排钢板桩围堰整体闭合后,其空间呈整体环形结构,相邻钢板桩结构在侧向“拉拽阻滑”及整体“空间尺寸效应”的影响下,其整体安全稳定性具有一定的安全富裕度。
3.3 有限元计算分析
采用MIDAS-GTS NX有限元软件建立三维模型进行模拟计算。本次研究取比一个隔仓长度稍长的42 m长围堰段进行三维建模研究。有限元模型中,钢板桩采用壳单元模拟,拉杆采用植入式梁单元,土体及抛石采用实体单元。土体本构采用Mohr-Coulomb模型。模型网格数为146 394,其中钢板桩单元数为9 049,围檩与拉杆单元数为483,基础及仓内土体单元数为136 862。围堰数值模型如图5所示。

图5 围堰有限元模型
模型边界约束为:模型前后侧边界施加沿z轴方向固定约束,模型左右侧边界条件为对称边界,土体表面为自由面不施加约束,模型底部施加沿垂直方向固定约束。模型施加荷载为正常运行工况下波浪荷载与静水压力。
根据有限元计算分析,在正常运行工况下双排钢板桩水平变位云图见图6,其外侧钢板桩最大水平位移发生在桩顶附近,最大计算值为139 mm。
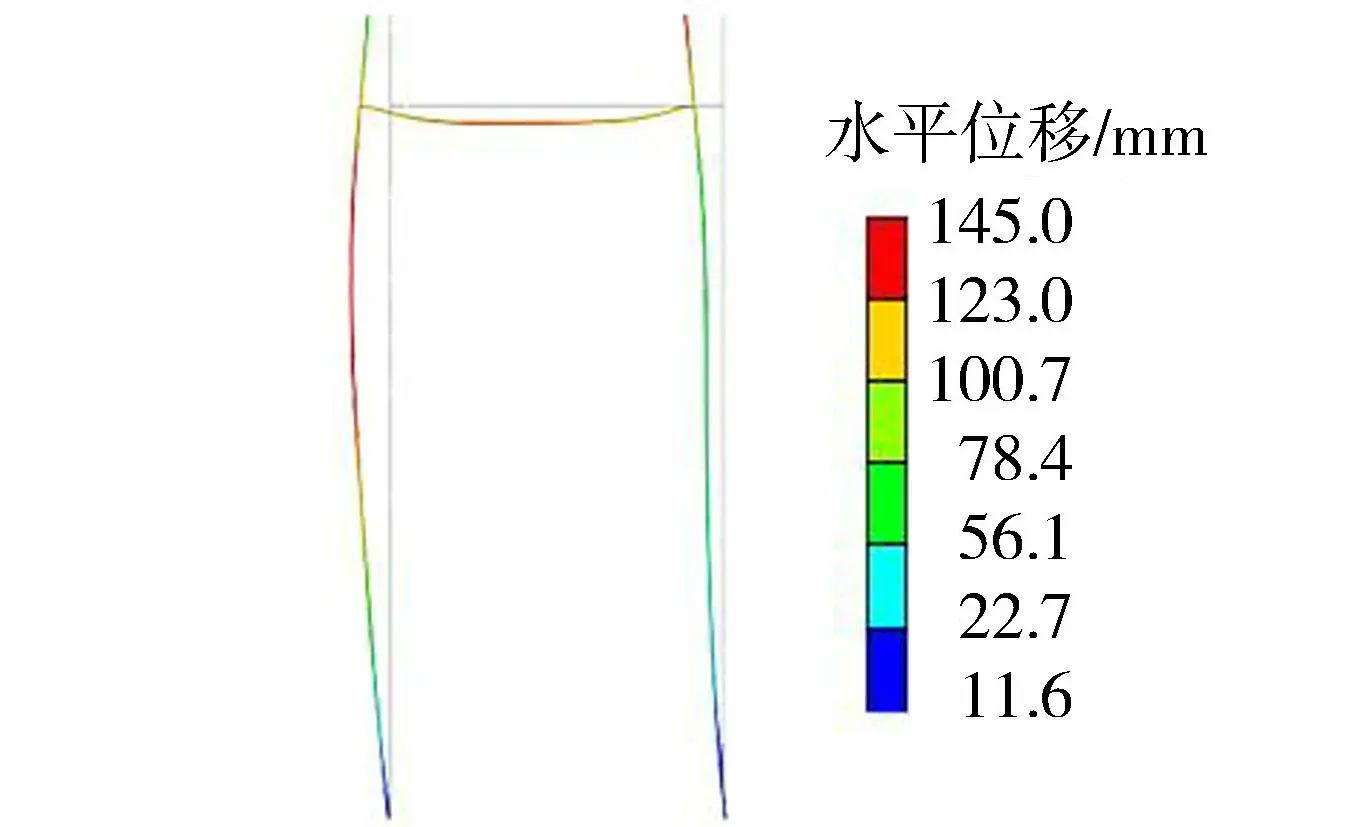
图6 钢板及拉杆水平位移计算结果
3.4 与实际监测资料对比分析
为了验证计算结构可靠性,将土体位移数值模拟结果与现场监测结果进行了对比,结果如图7所示。
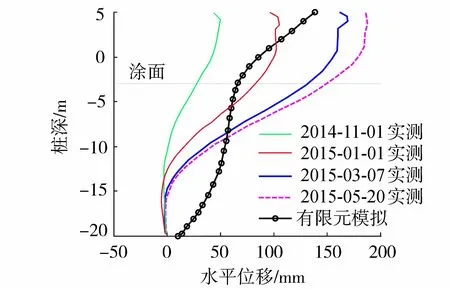
图7 外侧钢板桩位移对比
通过围堰内外侧土体位移的对比可知,实测最大水平变位值为187 mm,而有限元计算值为139 mm,其实测值比有限元计算中稍大,主要原因是工程实际运行中受潮位涨落的往复循环荷载作用影响所致,但其水平变位满足工程运行要求,因此双排钢板桩结构设计稳定可靠。
4 结 论
a. 对深厚淤泥地基中双排钢板桩围堰稳定计算进行建模,基于土力学理论,分别从钢板桩打设过程中屈曲稳定、运行工况下的抗剪切变形稳定、底部抗隆稳定、整体抗滑移稳定、抗倾覆稳定以及整体滑动稳定等方面进行控制分析,并给出相应稳定计算公式。
b. 对深厚淤泥地基土采用浅层换填砂“硬壳层”处理和增设内外侧抛石镇压层等措施,既可增加双排钢板桩结构水平抗力,又可加快淤泥土下卧层竖向排水固结,增加结构整体安全稳定性,同时给出了换填深度计算式。
c. 通过数学理论推导计算,给出了钢板桩最小入土深度Ld计算公式,便于工程实际应用。以浙江省某大型围垦工程水闸的双排钢板桩围堰工程为案例,依据文中提出的钢板桩最小入土深度Ld计算公式,得出最小入土深度建议值为17.01 m,与工程实际设计值18.50 m基本一致,认为该计算式基本满足设计要求。
d. 利用有限元计算软件,对本案例中双排钢板桩围堰结构进行数值模拟计算分析,并与钢板桩实际水平变位监测资料进行对比分析,认为该双排钢板桩围堰结构设计安全可靠,可为相关工程应用提供借鉴参考。
