基坑变形预测的改进供需优化算法-指数幂乘积模型

崔东文，李代华

(1.云南省文山州水务局,云南 文山 663000; 2.云南省水文水资源局文山分局，云南 文山 663000)

有效提高基坑变形预测精度对于判断基坑稳定性，预见周边建筑破坏程度，科学掌握基坑未来变形趋势具有重要意义[1]。目前应用于变形预测的方法有灰色预测法[2]、回归方法[3-4]、极限学习机法[5-6]、支持向量机法[7-8]、人工神经网络法[9-11]、组合预测法[12-13]等，均在基坑变形预测应用中取得一定的预测效果，但也存在不足：灰色预测法对原始数据依赖程度高、短期预测效果差；回归方法存在对异常值敏感、易过拟合等不足；极限学习机隐含层节点间连接权值和阈值的随机确定或人为给定制约了其应用；支持向量机存在惩罚因子、核函数等参数选取的困难[12]；BP、Elman等人工神经网络存在权、阈值等关键参数选取困难和受样本数量多少的制约；组合预测存在模型过于复杂、各模型权重确定困难等缺点。指数幂乘积(exponential power product，EPP)是利用预报因子与若干影响因子之间存在的指数幂乘积关系构建的预测模型，对高维、非线性系统具有较好的拟合、预测效果，但不足之处在于影响因子指数参数的合理选取。目前EPP模型在回归预测领域应用不多。

为进一步提高基坑变形预测精度，拓展基坑变形预测模型及方法，本文基于基坑变形预报因子与影响因子之间存在的指数幂乘积关系[12]，提出改进供需优化(improved supply-demand-based optimization)算法-EPP基坑变形预测模型(ISDO-EPP模型)，利用文献[14-16] 3个基坑变形预测实例对模型进行检验，以验证ISDO-EPP模型用于基坑变形预测的可行性和有效性。

1 ISDO-EPP模型

1.1 改进供需优化算法

供需优化(SDO)算法是Zhao等[17]于2019年受经济学供需机制的启发而提出的一种新型元启发式优化算法。该算法在数学上模拟了消费者的需求关系和生产者的供给关系，通过将供求机制之稳定模式和非稳定模式引入到SDO算法中，利用两种模式在给定空间中进行局部搜索和全局搜索求解待优化问题。与传统群智能算法相比，SDO算法收敛速度快、寻优精度高、调节参数少，具有较好的探索和开发能力。

参考文献[17]将SDO算法数学描述简述如下。

a. SDO算法初始化。假设有n个市场，每个市场有d种不同的商品，每种商品都有一定的数量和价格。市场中d种商品价格表示优化问题d维变量的一组候选解，同时将市场中d种商品数量作为一组可行解进行评估，如果可行解优于候选解，则可行解替换候选解。n个市场商品价格和商品数量分别用X、Y两个矩阵表示：

(1)

式中：xi和yi分别为第i个商品价格和数量；xij和yij分别为第j个商品在第i个市场中的价格和数量。

利用适应度函数分别对每个市场中的商品价格和数量进行评估，对于n个市场，商品价格和商品数量的适应度分别为：

(2)

b. 商品均衡数量与均衡价格。假设每种商品的均衡价格x0和均衡数量y0在每次迭代过程中都是可变的，从每个市场商品数量集合中选择一种商品数量作为其数量均衡向量，其市场适应度值越大，表示每个市场所选商品数量的概率就越大。同时，每个市场也可以根据其概率从商品价格集合中选择一种商品价格或以所有市场商品价格的平均值作为均衡价格。商品均衡数量y0表示如下：

y0=ykk=R(Q)

(3)

式中：f(yi)为商品数量yi的适应度值;R(·)为比选算子(roulette wheel selection)。

商品均衡价格x0表示如下：

(4)

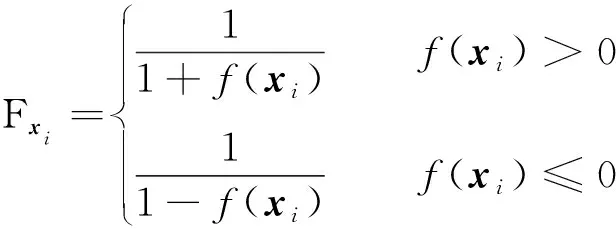
式中:f(xi)为商品价格xi的适应度值；r、r1为[0,1]中的随机数。

c. 供给函数和需求函数。依据均衡数量y0、均衡价格x0分别给出供给函数和需求函数：

yi，t+1=y0-α(xi，t-x0)

(5)

xi，t+1=x0+β(yi，t+1-y0)

(6)

式中：xi，t和yi，t分别为第t次迭代第i个商品价格和数量；α和β分别为需求权重和供给权重，通过调整α、β对均衡价格和均衡数量进行更新。

将式(5)插入式(6)中，可以将需求算式重写为

xi，t+1=x0-αβ(xi，t-x0)

(7)

供应权重α和需求权重β分别为

(8)

β=2cos(2πr)

(9)

式中：T为最大迭代次数。 用变量L表示供应权重α和需求权重β的乘积，可以得到：

变量L有助于SDO算法在勘探和开发之间平稳过渡。|L|<1属稳定模式，通过调整供应权重α和需求权重β得到均衡价格x0周围不同的商品价格，这些商品价格可以通过随机数r在当前价格和均衡价格之间随机变化，稳定模式机制强调“开发”以改善SDO算法的局部勘探能力。|L|>1属非稳定模式，它允许任何市场中的商品价格远离均衡价格，非稳定模式机制迫使每个市场在搜索空间中加强“勘探”未知区域以提高SDO算法的全局搜索能力。

为加快SDO算法的收敛速度，进一步改善SDO局部勘探性能和全局搜索能力，将供应权重α的求解算子改进如下：

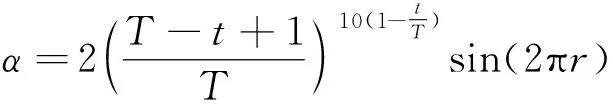
(11)

1.2 指数幂乘积模型

研究表明，基坑变形预测因子与其影响因子之间存在如式(16)所示的指数幂乘积(EPP)关系[18]：

(12)

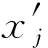
1.3 ISDO-EPP模型预测实现步骤

ISDO-EPP模型预测实现步骤归纳如下：

步骤1通过自相关函数法AFM、虚假最邻近法FNN确定实例基坑沉降数据的延迟时间和嵌入维数，构造EPP模型的输入、输出向量，合理划分训练样本和预测样本，利用式(17)对实例数据序列进行归一化处理；设定EPP模型指数参数aj的搜寻范围。

x′=(x-0.8xmin)/(1.2xmax-0.8xmin)

(13)

式中：x′为经过归一化处理的数据；x为原始数据；xmax和xmin分别为序列中的最大值和最小值。

步骤2确定优化目标函数。选用均方误差作为优化目标函数：

(14)

步骤3设置SDO算法市场群体数N，最大迭代次数T，问题维度，搜索空间。随机初始化商品价格xi和商品数量yi，令当前迭代次数t=0。

步骤4基于式(14)计算商品价格xi和商品数量yi的适应度值Fxi和Fyi，如果Fyi优于Fxi，则用yi代替xi，保存xbest为当前最优解。

步骤5利用式(15)、式(13)确定供应权重α和需求权重β。

步骤6对于每个市场，利用式(3)确定均衡数量y0；利用式(4)确定均衡价格x0。

步骤7利用式(5)更新商品数量yi；利用式(6)更新商品价格xi。基于式(14)计算商品价格xi和商品数量yi的适应度值Fxi和Fyi，如果Fyi优于Fxi，则用yi代替xi，保存xbest为当前最优解。

步骤8令t=t+1。判断算法是否达到终止条件，若是，输出最优解xbest，算法结束；否则重复步骤5～步骤8。

步骤9输出SDO算法全局最优解xbest，xbest即为EPP模型最佳指数参数aj。将指数参数aj代入EPP模型进行基坑变形预测。

ISDO-EPP算法流程见图1。

图1 ISDO-EPP算法流程

2 实例应用

2.1 数据来源及分析

本文以文献[14-16]3个基坑变形预测为例进行实例验证。其中，实例1数据来源于文献[14]，共有40个周期的沉降监测数据；实例2数据来源于文献[15]，共有20个周期的沉降监测数据；实例3数据来源于文献[16]，共有15个周期的沉降监测数据。首先利用AFM确定沉降数据延迟时间，经分析，当延迟时间为1时3个实例的自相关系数最大，分别为0.938、0.779、0.786，因此确定沉降数据的延迟时间为1。其次在延迟时间为1的条件下采用FNN确定沉降数据的嵌入维数，见图2。从图2可以看出，当嵌入维数分别为3、4、2时，3个实例的虚假最邻近的比例均为0，小于1%，说明由该嵌入维确定的重构吸引子不会再出现因投影到低维空间而发生重合现象，即当延迟时间为1、嵌入维数分别为3、4、2维时，3个实例具有最佳预测效果。最后，在延迟时间为1、嵌入维数分别为3、4、2条件下，利用实例1前3期、实例2前4期、实例3前2期监测数据预测实例1第4期、实例2第5期、实例3第3期基坑沉降值，并选取实例1、实例2前32期、前11期实测数据作为训练样本，后5期数据作为预测样本；选取实例3前10期实测数据作为训练样本，后3期数据作为预测样本。限于篇幅，基坑变形预测因子与影响因子的输入、输出矩阵从略。

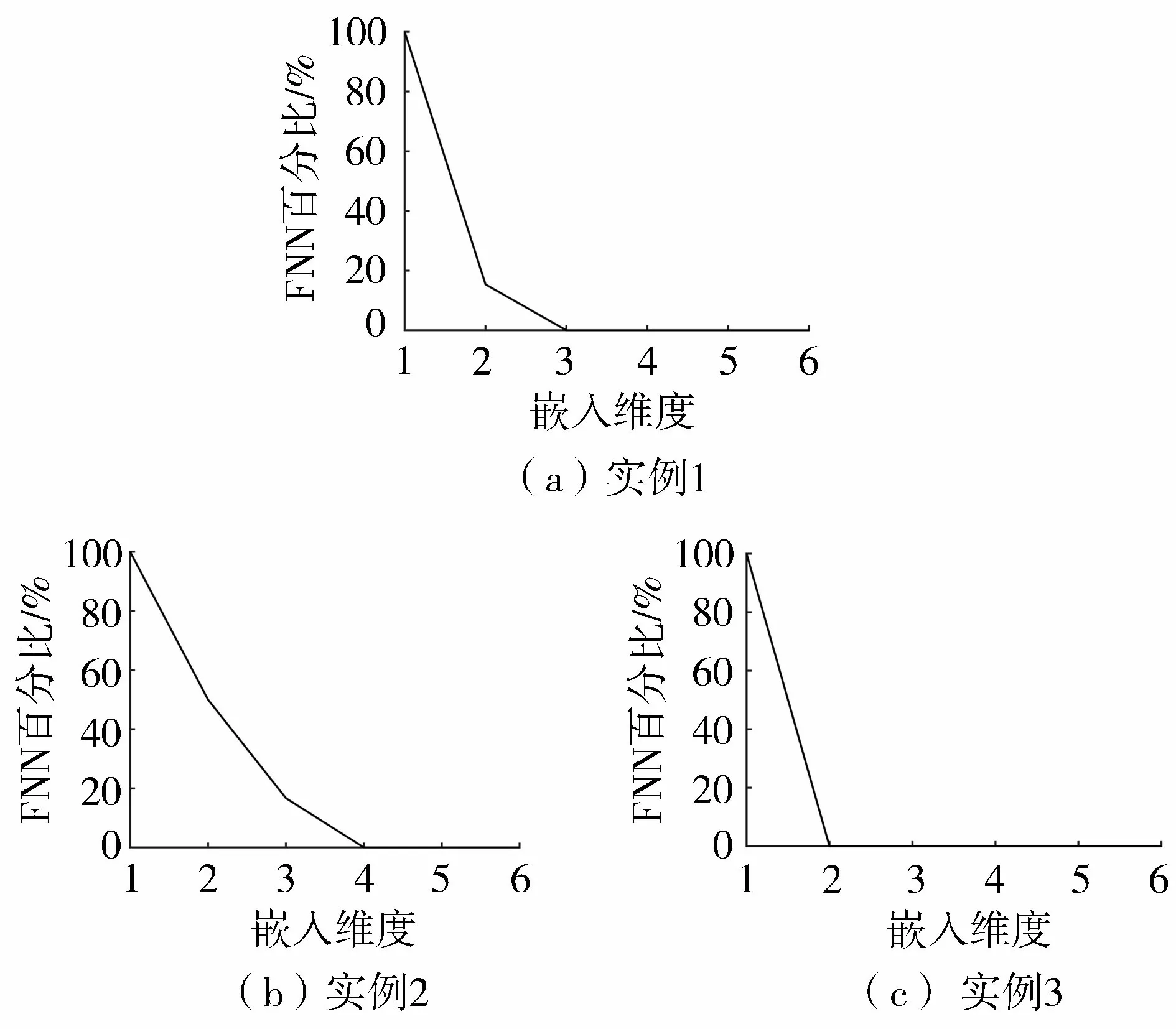
图2 基坑监测数据虚假邻近点法结果

2.2 算法验证

2.2.1标准测试函数仿真验证

为验证ISDO算法在高维(30维)和低维(5维)条件下寻优能力，利用ISDO算法对Sphere、Schwefel 2.22、Schwefel 2.21、Griewank、Rastrigin、Ackley 6个典型测试函数进行仿真验证，并与SDO、WOA、GWO、MSA、PSO算法的仿真结果进行比较。上述6个函数变量取值范围分别为[-100,100]、[-10,10]、[-100,100]、[-600,600]、[-5.12,5.12]、[-32,32]，维度为30维和5维，理论最优解值均为0。其中，函数Sphere、Schwefel 2.22、Schwefel 2.21为单峰函数，主要用于测试算法的寻优精度；函数Griewank、Rastrigin、Ackley为多峰函数，主要用于测试算法的全局搜索能力。基于Matlab 2018a M语言实现6种算法对6个典型测试函数的20次重复寻优，并从平均值、标准差2个方面进行评估，见表1。实验参数设置如下：6种算法最大迭代次数最大迭代次数T=200，群体数目N=50。其中WOA对数螺旋形状常数b=2；MSA勘探蛾数量np=5； PSO算法惯性权重wmax、wmin分别取值0.9和0.6，自我学习因子c1、社会学习因子c2均取值2.0。其他参数采用各算法默认值。

a. 对单峰函数Sphere、Schwefel 2.22，ISDO算法在高维和低维情况下20次寻优精度略优于MSA、SDO算法，优于WOA、GWO算法，远优于PSO算法。对于梯度函数Schwefel 2.21，ISDO算法在高维情况下20次寻优精度优于MSA、SDO算法，远优于WOA、GWO、PSO算法；在低维条件下，ISDO算法在高维情况下20次寻优精度略优于MSA、SDO算法，优于GWO算法，远优于WOA、PSO算法。对于单峰函数，ISDO算法在高维和低维条件下均表现出较好的寻优精度。

b. 对于多峰多模态函数Griewank，在高维和低维情况下，ISDO、MSA 算法20次寻优均获得了理论最优值0，寻优精度优于SDO算法，远优于WOA、GWO、PSO算法。对于易陷入局部极值多峰函数Rastrigin，在高维和低维情况下，ISDO、SDO、MSA算法20次寻优均获得了理论最优值0，寻优精度远优于WOA、GWO、PSO算法。对于连续旋转不可分多峰函数Ackley，ISDO、SDO算法 20次寻优均获得了相对理论最优值8.88×10-16，寻优精度优于MSA、WOA、GWO算法，远优于PSO算法。对于多峰函数，ISDO算法在高维和低维条件下均表现出较好的全局搜索能力。

c. 从6个标准测试函数的仿真验证结果来看，ISDO、MSA、SDO算法的寻优精度基本不受维度影响，对于较难优化的Schwefel 2.21、Griewank、Rastrigin函数，WOA、GWO、PSO算法的寻优精度受维度变化影响较大。综合来看，6种算法寻优精度由高至低依次是：ISDO、MSA、SDO、GWO、WOA、PSO算法。

表1 函数优化对比结果

2.2.2实例目标函数优化验证

为证验证ISDO、SDO、WOA、GWO、MSA、PSO算法在实例应用中的优化性能，利用上述构造的3个基坑预测侍优化目标函数，即式(14)对ISDO等6种算法的优化性能进行验证。其中，EPP模型参数aj的搜索范围为[-5,5]，最大迭代次数T设置为200和500，其他参数设置、评估指标同上。实例优化结果见表2。

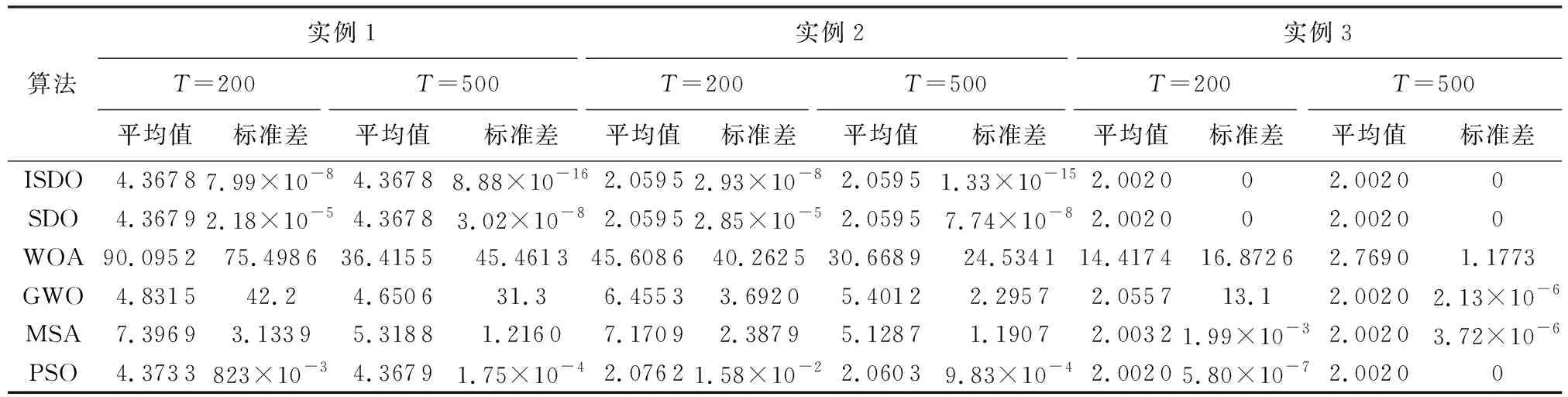
表2 应用实例目标函数优化对比结果

对于实例1，ISDO算法无论在迭代200次还是500次条件下，20次寻优目标函数最优值均为4.367 8，标准差小于8.00×10-8，寻优效果略优于同等条件下的SDO算法，优于PSO、GWO算法，远优于MSA、WOA。对于实例2，ISDO、SDO算法不同迭代条件下20次寻优目标函数最小值均为2.059 5，优于PSO算法，远优于GWO、MSA、WOA算法。对于实例3，由于序列较短和待优化维较低，ISDO、SDO、PSO算法20次寻优目标函数最小值均为2.002 0，标准差均为0，寻优效果优于同等条件下的MSA、GWO算法，远优于WOA。

在上述6个标准测试函数中寻优效果表现较好的MSA、GWO、WOA在3个实例应用的优化中表现较差，寻优效果甚至低于PSO算法，可认为寻优失败。应用实例最佳参数寻优验证了“没有免费午餐定理”，即没有一种算法能解决所有优化问题。综合来看，6种算法在实例应用中寻优精度由高至低依次是：ISDO、SDO、PSO、MSA、GWO、WOA。

可见，基于供应权重改进的ISDO算法能进一步改善SDO算法在勘探和开发之间平衡能力，提高SDO算法的收敛速度和全局搜索性能；ISDO算法不仅在标准测试函数高维和低维条件下具有较好的收敛精度和全局搜索能力，而且在实例目标函数优化中同样表现出良好的寻优效果和稳健性能。

2.3 实例预测及分析

在最大迭代次数为200条件下分别构建ISDO-EPP、ISDO-SVM、ISDO-BP模型对上述3个实例基坑变形进行预测。选取平均相对误差绝对值MRE、平均绝对误差MAE作为评价指标，利用此3种模型对3个实例基坑变形进行预测，结果见表3，并给出训练-预测相对误差效果图，见图3。其中SVM、BP参数设置如下：SVM模型惩罚因子C∈[0.1,1000]、核函数参数g∈[0.1,1 000]、不敏感系数ε∈[0.001,0.1]，交叉验证折数V=3；3个实例BP模型网络结构分别设置为3-5-1、4-7-1、2-3-1，隐含层和输出层传递函数均分别采用logsig和purelin，训练函数均采用trainlm，设定期望误差为0.001, 最大训练轮回为100次，搜索空间为[-1,1]。

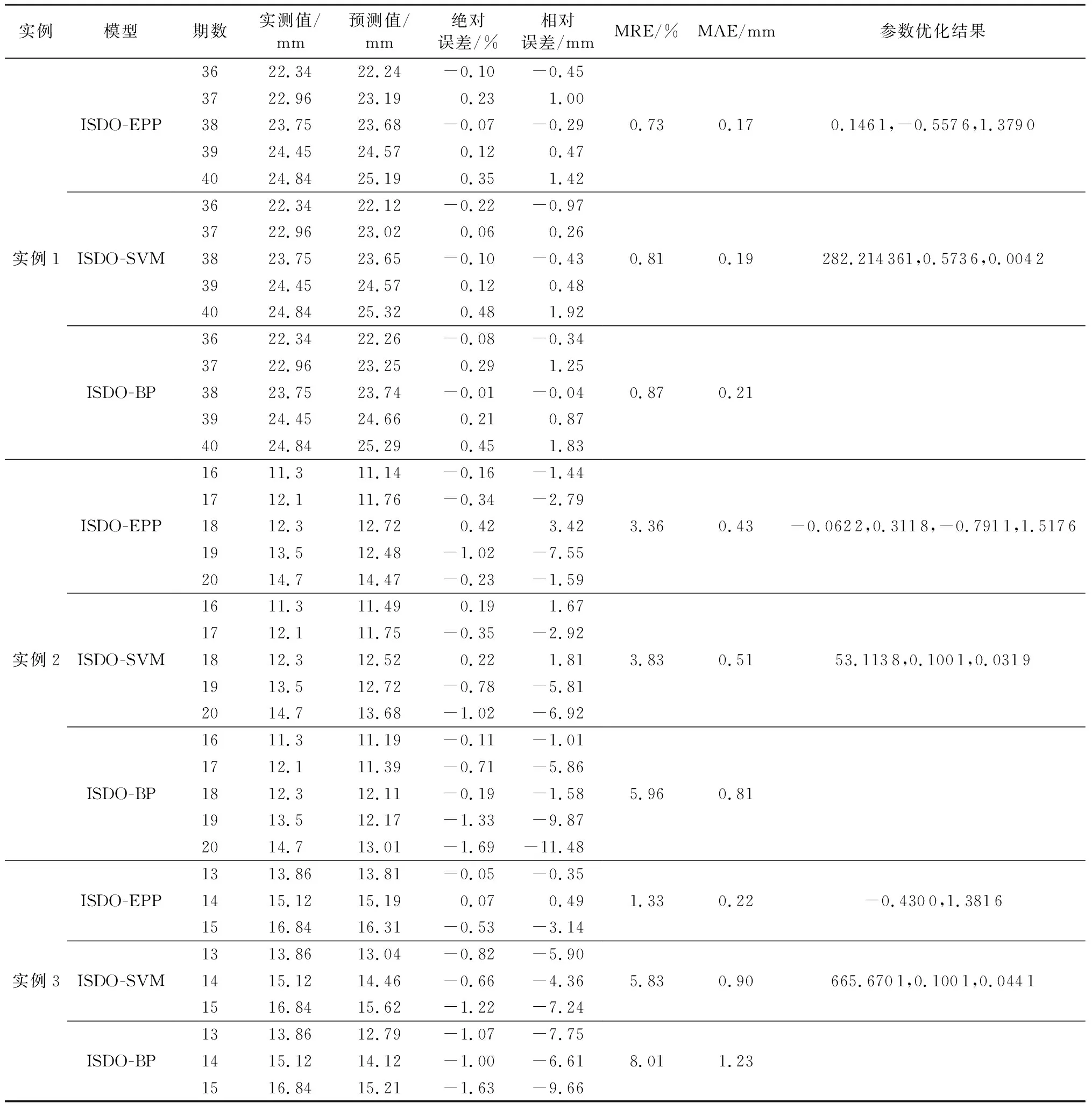
表3 各基坑变形预测模型效果对比

图3 3种模型拟合预测相对误差

依据表2、表3及图3可以得出以下结论：

a. ISDO-EPP模型对3个实例预测的MRE分别为0.73%、3.83%和1.33%，精度分别较ISDO-SVM模型提高9.9%、12.3%和77.2%，较ISDO-BP模型提高了16.1%、43.6%、83.4%；3个实例的MAE分别为0.17 mm、0.51 mm和0.22mm，精度分别较ISDO-SVM模型提高10.5%、15.7%和75.6%，较ISDO-BP模型提高19.0%、46.9%和82.1%，具有较好预测精度和泛化能力，表明ISDO算法能有效优化EPP模型的指数参数，ISDO-EPP模型用于基坑变形预测是可行和有效的，模型及方法可为大坝变形等相关预测研究提供新的途径和方法。

b. 从图3和表2、表3来看，ISDO-EPP模型的拟合精度(目标函数优化结果)、预测精度均优于ISDO-SVM、ISDO-BP模型，表明ISDO-EPP模型具有较好的拟合、预测精度；从表2来看，ISDO算法20次寻优EPP模型目标函数的结果均相同，即优化参数结果相同，表明ISDO-EPP模型具有较好的稳健性能。

c. 从3种模型对3个实例预测结果对比分析来看，ISDO-EPP模型具有较好的适用性和预测效果，预测结果是可信和合理的。ISDO-BP模型预测效果并不十分理想，原因在于训练样本过少，难以充分训练模型，在实际应用过程中易出现“过拟合”或“欠拟合”现象，导致模型实用性能变差。

3 结 论

a. 提出改进供需优化(ISDO)算法，通过6个典型测试函数在高维和低维情况下和3个实例目标函数对ISDO算法的寻优能力进行验证，并与SDO、WOA、GWO、MSA、PSO算法的寻优结果进行比较。结果表明：ISDO算法不仅在标准测试函数高维和低维条件下具有较好的收敛精度和全局搜索能力，而且在实例目标函数优化中同样表现出良好的寻优效果和稳健性能。

b. 基于AFM和FNN确定沉降数据延迟时间和嵌入维数，构建基坑变形预测的输入、输出向量；利用ISDO算法优化EPP模型指数参数，提出ISDO-EPP模型，并构建ISDO-SVM、ISDO-BP模型作比较模型，以3个基坑变形预测实例进行对比验证。结果表明：ISDO-EPP模型预测精度和预测效果均优于ISDO-SVM、ISDO-BP模型，具有较好拟合-预测精度和稳健性能，表明ISDO算法能有效优化EPP模型指数参数，ISDO-EPP模型用于基坑变形预测是可行和有效的。

c. 验证表明，在标准测试函数中寻优效果表现较好的MSA、GWO、WOA在3个实例应用的优化中表现较差，寻优效果甚至低于PSO算法，可认为寻优失败。再次验证了“没有免费午餐定理”，即没有一种算法能解决所有优化问题。