基于瑞雷波速的碾压混凝土压实效果评价

2020-08-10屈嘉程田正宏

水利水电科技进展 2020年4期

屈嘉程，田正宏，孙啸，洪燕

(河海大学水利水电学院，江苏南京 210098)

碾压混凝土坝的施工质量直接关系到大坝长效运行安全，有效控制坝体填筑压实质量是保证大坝安全的关键[1]。目前，碾压施工层主要通过核子密度仪现场采样检测控制碾压过程混凝土压实度指标。这种方法现场采样点少，随机性强，耗费时间甚至影响施工连续性，无法对仓面碾压层的压实质量进行全面准确的评价[2-3]。瑞雷面波作为广泛应用的压实质量评价方法具有检测快速、无损、分辨率高等特点，结合其传播速度与介质密度的相关性，在公路、铁路路基等压实质量无损检测中应用普遍。近些年来，瑞雷面波被引入碾压混凝土坝压实质量评价研究中，一定程度上弥补了传统抽样检测方法随机性大、可靠性低等不足，但实际应用中仍然存在以下关键问题：①鉴于施工现场工况复杂，采集信号混杂多重噪声源，准确的瑞雷波特征难以有效提取，重复采样、多次叠加取平均的传统去噪方法往往效果不佳[4]；②利用瑞雷波速表征压实效果仍停留在定性分析的阶段，无法定量评价碾压测点压实度；③瑞雷波信号采样仍属于单点试验法，离散波速值无法全仓面表征碾压热层的压实指标。鉴于此，本文尝试结合切比雪夫Ⅰ型高通滤波和小波阈值去噪的信号提纯方法，有效消除施工过程中随机干扰噪声来源，获得更加准确可靠的检测瑞雷波速，并建立基于瑞雷波速的碾压层压实质量评价方法，实时预测仓面任意点的压实质量，量化波速与压实指标的相关度，并运用Kriging空间插值法获取全仓面的压实合格率和云图分布，以期为实际施工中全局量化质量缺陷后的弥补措施提供有效指导。

1 基于瑞雷波去噪技术的压实质量评价方法

1.1 瑞雷波去噪方法和波速模型计算

碾压施工现场采集到的瞬态激振信号通常由体波、瑞雷面波和其他施工干扰噪声在碾压热层干涉叠加而成[5]。在激振产生的应力波信号中，通常瑞雷波能量占全部激振能量2/3左右，且瑞雷波能量衰减慢，传播距离远。因此在采集波形过程中，将振源设置于远离一侧加速度传感器的恰当位置，通过能量特征差异可有效弱化其他应力波成分影响。相较而言，施工现场的多重噪声对瑞雷波信号采集干扰更加显著。根据已有碾压混凝土坝施工研究和现场信号采集分析，干扰噪声成分主要分为以下3种：①振动碾产生的40～50 Hz干扰噪声；②碾压混凝土坝体自身0～50 Hz的固有频率[6]；③高频采集噪声和环境白噪声。为此，采用高通数字滤波器，设置阻带截止频率53 Hz，通带截止频率57 Hz，尽可能滤除53 Hz以下的低频波，可极大地消除低频噪声对瑞雷波信号干扰。此外，采用小波阈值去噪对因加速度传感器高频采集特性引起的高频噪声和环境白噪声进行抑制处理，可有效提取出较为纯净的瑞雷波特征信号。

1.1.1切比雪夫Ⅰ型高通滤波

a. 滤波器选择。在数字信号处理中，常用信号滤波器主要有巴特沃斯滤波器、切比雪夫Ⅰ或Ⅱ型滤波器、椭圆滤波器、贝塞尔滤波器等。设相同阶数且阻带下限归一化频率为0.6的情况下，4种滤波器的幅频特性曲线如图1所示。可以发现，相较于其他滤波器，切比雪夫Ⅰ型滤波器具有过渡带衰减速度快、通带等纹波特性以及阻带稳定性好等特点，满足瑞雷波去噪功能要求。故本文选用切比雪夫Ⅰ型高通滤波消除低频噪声对有效瑞雷波信号的干扰影响。

图1 4种滤波器的幅频特性曲线

b. 传递函数。传递函数是指零初始条件下线性系统响应(输出)量与激励(输入)量的Laplace变换之比，是描述线性系统动态特性基本数学工具之一。高通滤波器的传递函数通常需要通过频率转换，由低通滤波器的传递函数变换获得。切比雪夫Ⅰ型低通滤波器归一化后的传递函数为

(1)

式中：G(p)为传递函数；ε为通带纹波系数；N为低通滤波器阶数；pi为滤波器极值椭圆左半平面极值点，也是传递函数特征方程零点。经过频率转换后，得到切比雪夫Ⅰ型高通滤波器归一化后的传递函数Ha(s)：

Ha(s)=G(p)|p=Ωs/s

(2)

式中:Ωs为通带截止频率。得到滤波器的传递函数只需确定相应的技术指标参数，即通、阻带截止频率和衰减系数。依据现场干扰噪声频率分布，本文拟确定阻带截止频率53 Hz，通带截止频率57 Hz，通带最大衰减幅值0.1 dB，阻带最大衰减幅值40 dB，则可去除阻带频率范围内的各种低频噪声。

1.1.2小波阈值去噪

由于加速度传感器误差、测量精度、环境白噪声等影响，采集到的瑞雷波信号中不可避免地混杂有随机高频噪声，仅通过高通滤波器进行信号处理难以满足去噪要求。小波变换是一种信号时间-尺度(时间-频率)分析方法，它具有多分辨分析的特点[7]，而且在时频两域都具有表征信号局部特征的能力，很适合于分析非平稳的信号和提取信号的局部特征。因此，针对残留的随机噪声，选用小波阈值去噪法进行二次去噪处理。

小波阈值去噪法的效果受多方面影响，其中阈值和阈值函数选择、小波基种类筛选、分解层数确定是关键因素。尤其是以何种规则选取阈值和阈值函数，在某种程度上直接影响信号去噪效果好坏。

a. 阈值函数。在对小波系数作阈值量化处理时，常采用的阈值函数有两种：硬阈值函数和软阈值函数[8]。考虑到硬阈值去噪后小波系数在阈值处具有不连续性和跳跃性，导致过滤噪声重构信号不平滑，且可能存在尖峰，因此本文采用软阈值去噪，以保证去噪后信号具有较高信噪比，又不失平滑性，软阈值函数公式为

(3)

式中：wλ为修正小波系数；w为小波系数；λ为阈值。

b. 阈值。阈值过大或偏小都将对信号的去噪效果产生影响。通过波速仪现场测试发现，高频采集噪声和环境白噪声广泛分布于高频区。阈值过大，信号中有效高频成分被过滤，重构信号失真度较大；阈值过小，广泛分布于信号中的高频噪声则难以消除，使去噪后信号与原始信号较为相近，达不到去噪效果。为此，本文提出改进Minmax准则的阈值选择方法，利用Minmax阈值不易消除信号有效成分的优势，结合现场采样环境设置相关比例因子k，能最大程度降低噪声对瑞雷波干扰。具体公式为

式中：M为波速信号的采样点数；j为分解尺度；cj(k)为分解尺度j条件下小波系数绝对值的中值。由试验数据分析确定k=2。

c. 最佳分解层数。研究[9-10]表明，在信号去噪过程中，某些误差指标(如均方根误差(RMSE))存在收敛特性，即达到最佳分解尺度后，变化率显著降低并趋于平稳。该特性与聚类分析有效性评价中经典的Hubert’Γ统计量确定最佳聚类数目具有类似特征[11]。借鉴其方法，通过识别加权融合指标[12]变化的拐点来确定最佳分解尺度，进行了8个分解层次的加权融合指标比较，并认为当指标变化曲线首次出现拐点时，其分解尺度达到最佳，结果见图2。

图2 不同分解层数的加权融合指标变化

从图2可以看出，当分解层数达到4层时，加权融合指标出现了较明显拐点，且变化曲线出现了明显收敛趋势，表明小波基分解尺度在4层以上时去噪效果最佳。考虑数据传输实时性，并降低系统运算量，在此拟确定分解层数为4层。

d. 小波基。相关研究[13]表明，针对同一信号不同小波基的去噪效果比较而言，基于信噪比(SNR)、RMSE的评价方法能够得到合理的评价结果。一般认为，SNR越高，RMSE越小，滤波去噪效果越好。SNR和RMSE公式为

(5)

(6)

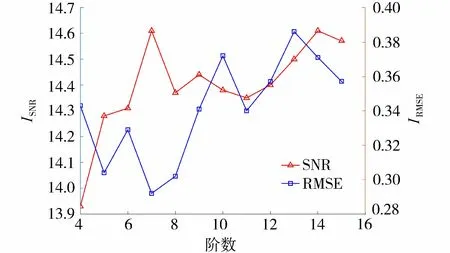
图3 db小波基去噪效果对比

1.1.3基于SASW的瑞雷波速计算模型

波速仪现场检测过程中，首先利用加速度传感器采集振源激振出的两道瑞雷波信号，将采集的两列波形信号分别通过切比雪夫Ⅰ型高通数字滤波器滤除低频噪声、小波阈值去噪抑制高频采集噪声和环境白噪声，然后通过表面波谱分析法(spectral analysis of surface waves，SASW)获取瑞雷波速值，并结合GNSS-RTK单定位系统和远程无线传输系统，实现了测点处波速值、时空信息、区域信息等参数实时上传云服务器数据库并存储调用。

SASW的波速计算原理是将滤波处理后的两道瑞雷波信号经傅里叶变换、互谱分析得到相位谱，通过式(7)计算瑞雷波相速度：

(7)

式中：vR(f)为瑞雷波相速度；θ(f)为相位谱；f为频率；L为加速度传感器间距。瑞雷波在分层介质中具有高度的频散特性，但由于本文主要研究碾压热层的压实质量评价，瑞雷波的频散性在试验中并不显著，因此本文选用瑞雷波相速度的均值作为压实度评价指标的波速表征值：

(8)

式中：vR为瑞雷波速表征值；n为频带点数。

1.2 碾压混凝土压实质量评价体系

1.2.1压实质量评价指标

碾压混凝土坝施工压实质量评价的效果与选取的质量控制参数密切相关。已有研究[14-15]表明，在大坝碾压施工中，影响压实质量的因素众多，主要分为碾压参数控制指标(如碾压遍数、碾压机械速度、振动状态、压实厚度等)和料源参数控制指标(如含湿率、级配等)两种，若不加筛选地将所有因素纳入考虑范围，必然会加大施工压实质量评价难度，从而影响参数控制效果。因此，综合考虑各参数的可表征性、可获取性和参数间的耦合特性，参考近年来一些研究中利用其他综合特征指标(如sound compaction value(SCV)、compaction meter value(CMV))表征压实质量取得的良好效果，本文选取碾压热层瑞雷波速和拌合料含湿率[16]作为模型评价指标。在弹性波理论中，瑞雷波在介质中传播速度可由下列计算公式表示：

(9)

式中:σ为泊松比。

由式(9)可知，瑞雷波速理论上只与介质的物理力学性质密切相关。因此可以通过碾压后介质物理参数的理论范围确定瑞雷波速的有效范围，进而消除现场采样时因试验操作不当以及振源频带异常等不确定因素而导致的波速测值异常。

1.2.2压实质量评价方法和步骤

目前，一些学者在压实质量评价研究中采用了回归模型[17-18]和地质统计学分析方法[19]，以综合特征指标(CMV、SCV)表征土方工程中填筑材料的不同压实状态，并对碾压施工区域内任意位置的压实质量进行评价，可以有效地量化空间均匀程度，识别欠碾压区域，提高碾压作业过程控制。因此，本文采用回归评价模型(单变量或多变量回归)和地质统计学分析方法(Kriging插值)，结合瑞雷波信号去噪和波速提取方法，提出基于瑞雷波速的压实质量评价方法。具体评价步骤如下:

步骤1现场数据采集。根据预先设计好的试验方案进行数据采集，试验前将每条碾压条带分为若干个等宽试验块；然后采用自主研发的波速测试仪，通过上述的瑞雷波信号去噪和SASW计算模型获取波速值；使用核子密度仪、含湿率仪对测点压实度与含湿率等参数进行采集；最后得到若干组现场试验数据。

步骤2参数相关性分析。分析碾压混凝土料压实度、瑞雷波速和含湿率之间的相关性。

步骤3回归模型建立和精度检验。根据相关分析结果，建立压实度回归统计模型(单变量或多变量回归)，并进行显著性检验。基于不同回归模型的预测准确性，并考虑模型构建使用便捷性，选择适合的回归模型来分析碾压混凝土热层压实指标。

步骤4压实质量的地质统计分析与仓面总体评价。现场仓面采样点一般选为等距离散点，预测的压实度只是对压实指标的离散分布估计。因此采用Kriging插值对碾压条带任意位置的压实指标进行连续估计。根据式(10)对压实质量进行整体评估：

(10)

式中：P为碾压区域压实质量合格率；SQ为压实度满足要求的碾压区域面积；SA为碾压区域总面积。

利用渐变色带结合图形可视化技术，可以更加直观地反映碾压仓面的压实度指标量化分布。基于上述评价方法，可有效评估碾压混凝土层的全局量化压实质量，指导实际施工中质量缺陷的有效弥补。

2 实例应用

乌弄龙水电站位于云南省境内的澜沧江上游河段，电站枢纽为二等大(2)型工程，枢纽建筑物主要由碾压混凝土重力坝、电站进水口、地下厂房系统、泄洪表孔、冲沙泄洪底孔等组成。拦河坝为碾压混凝土重力坝，坝顶高程1 909.5 m，最大坝高137.5 m，坝顶轴线长度 247.10 m。选取大坝左岸10号坝段碾压区的第4施工仓第11层为试验区域。试验时，在仓面中心区域取3条碾压条带(以1、2、3号标识)，每条碾压条带宽6 m，总长30 m，有效长度27 m，间隔3 m选取一个样本采集点，进行参数(压实度、含湿率、瑞雷波速)数据的采集，测点分布示意图见图4，利用采集的样本参数进行相关性分析，建立回归预测模型，最终评价全仓面压实质量。

图4 试验测点分布示意图(单位：m)

2.1 信号去噪提取效果

对于实际信号去噪效果的评价不宜采用SNR，而应从实际应用出发，选取同一传播方向上两道信号的相干系数作为评价指标，表征信号之间相互关联程度。相干系数越接近1，表明去噪效果越好。施工现场信号采集过程中，采用前文所述去噪方法及对应指标参数，利用Matlab分别提取去噪前后瑞雷波波形图像(图5)，可以看出去噪后信号在非激振时段波形平滑、无随机干扰噪声，同时激振时段内信号得以很大程度保留。为验证瑞雷波信号去噪效果，计算去噪前后的相干系数(图6)，可见在高通滤波器通带内(57 Hz以上)频率点的相干系数明显改善，表明原始信号去噪后，两道瑞雷波信号受噪声干扰较小，相似度高，去噪效果较好。

图5 瑞雷波去噪前后时域信号对比

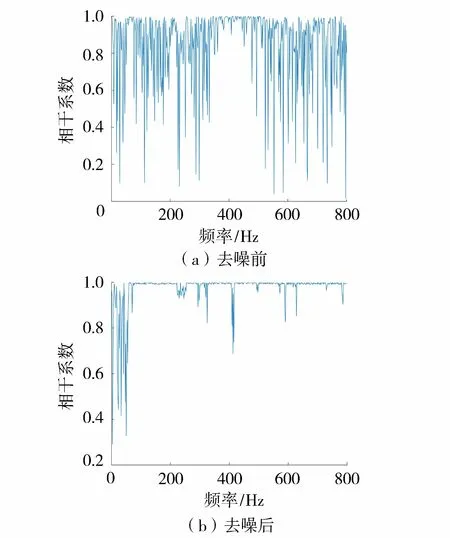
图6 瑞雷波去噪前后相干系数对比

图7 1号碾压条带瑞雷波去噪前后波速分布

试验时，振动碾在碾压条带上碾压规定遍数后，用波速仪检测选定位置间距的瑞雷波速。图7为1号碾压条带碾压8遍后测得的去噪前后测点波速分布。从图7可以看出，未去噪的各测点波速值分布离散程度很大(有些波速值脱离理论范围)，无法作为参数准确表征碾压混凝土层的压实度指标。而经过去噪处理后的波速值分布均匀，且在理论范围之内，具有良好表征性。考虑到实际碾压条带压实不均匀，部分区域可能存在欠碾情况，因此个别波速值出现异常波动。

2.2 参数相关性分析

在1、2号条碾压条带上采集获得40组瑞雷波速、含湿率和压实度数据，剔除异常点后取其中35组有效样本点作为独立数据集。分别对坝料压实度与瑞雷波速、含湿率进行回归分析，结果见图8。

图8 压实度、瑞雷波速与含湿率的回归分析结果

由图8可见，压实度与瑞雷波速线性拟合的决定系数R2为0.874 1，具有高度相关性，因此将瑞雷波速作为评价模型构建的主要因素；压实度与含湿率相关性较高，且二次拟合优于线性拟合；压实度随着含湿率的增大而增大，超过特定含湿率时，则随着含湿率的增大而减小；碾压混凝土的振动压实存在着一个最优含湿率问题，符合实际情况。

2.3 回归模型的选择

通过以上分析可知，瑞雷波速和含湿率两个参数与碾压混凝土压实度之间均存在相关性，因此选择这两个参数建立压实质量的3组回归评价模型，并且从这3个回归模型中选择合适的模型来估算碾压混凝土坝的压实质量。使用上述35组样本数据，通过函数拟合建立3个回归模型：①把瑞雷波速视为独立变量的单变量线性回归模型Ⅰ；②假设瑞雷波速和含湿率相互独立的多元非线性回归模型Ⅱ；③为了更好地进行精度对比分析，补充建立了多元线性回归模型Ⅲ。具体的模型拟合回归方程见表1，可以看出，3组模型的决定系数均大于0.8，在显著性水平0.05下，总体F检验为0.000，且引入含湿率的非线性回归模型R2最大，说明模型Ⅱ的回归方程对于样本的拟合优度最大，回归显著。

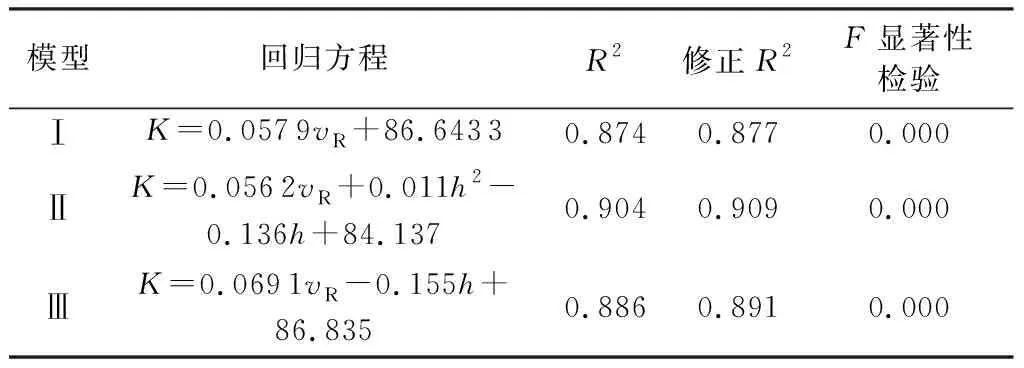
表1 回归模型及其统计学指标

图9 验证样本拟合结果

为比较3组回归模型的预测精度，采用交叉验证对模型的评价结果进行分析。通过现场采集试验获取总共60组样本，选取1、2号碾压条带的40组样本数据作为训练集Strain拟合得到不同的回归假设函数hi，3号碾压条带的20组样本数据作为交叉验证集Scv，利用Scv对3组拟合回归模型进行压实度预测，与实测值进行对比，以验证模型精度，结果见图9。采用SD、MAE、RMSE作为评价指标，对比3组回归模型的精度，结果见表2。3组模型预测精度高、误差评价指标接近，在引入含湿率指标来补充解释压实度的变异成分后，模型Ⅱ的MAE、RMSE分别下降5.59%、7.27%，模型Ⅲ的MAE提高4.19%、RMSE下降5.17%，说明考虑含湿率的非线性回归模型能够有效降低误差指标，提高预测精度，因此选取模型Ⅱ对仓面试验点进行压实度预测。

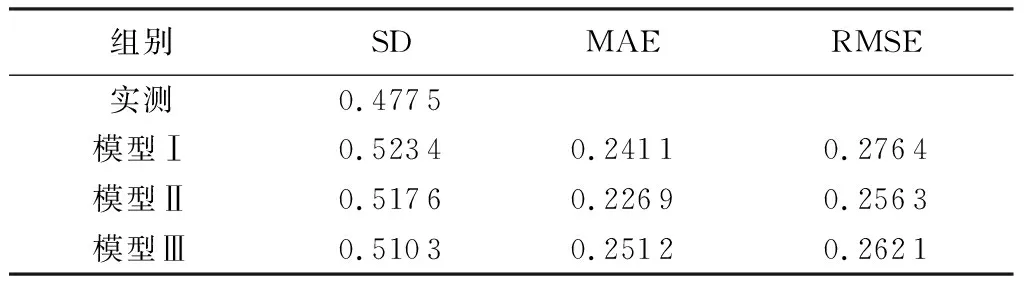
表2 3组预测模型精度评价指标对比

2.4 全仓面压实质量评价

交叉验证和F检验的结果表明，瑞雷波速的多元非线性回归模型可应用于压实质量评价。基于模型Ⅱ和智能反馈系统，结合Kriging插值法建立混凝土全仓面碾压层压实质量评价模型。首先，将某30 m×30 m的碾压层仓面分成100个3 m×3 m的网格，以网格中心点作为离散点，获取样本坐标数据(x,y)，通过模型Ⅱ进行离散点压实度预测得到z坐标，并将(x,y,z)坐标作为自变量导入云图生成软件；其次，采用Kriging插值法进行区域性变量优化赋值，考虑相邻坐标的预测结果及其空间分布特征，使插值结果更精确、更符合实际；最后，生成压实质量分布云图(图10)。DL/T 5112—2009《水工碾压混凝土施工规范》中规定，碾压内部混凝土压实度不应小于97%，根据式(10)，得到仓面碾压合格率为95.69%。针对压实质量评价云图中显示的质量缺陷区域，应进行及时补振，以确保仓面的填筑碾压效果达到精细控制施工质量的目的。