树立五种意识破解恒成立问题

浙江省金华第一中学(321015) 黄锦龙

既含参数又含变量的不等式恒成立问题之所以备受命题者的青睐,一方面是这类问题把不等式、函数、方程、几何等内容有机结合起来,在知识的交会处命题,具有知识点多、综合性强等特点,能体现出很好的区分度与选拔功能;另一方面是此类问题条件复杂,切入点难发现,能很好地检测学生的数学能力.学习解决好不等式恒成立问题,能巩固基础知识,训练基本技能,感悟基本思想,丰富基本活动经验,提高从数学角度发现和提出问题的能力、分析和解决问题的能力,促使数学学科核心素养落地开花.本文通过实例,以问题为导向,用五种意识对破解不等式恒成立问题作出解析,供读者参考.

1 特值探路,验证结论快捷解

例1(2018年3月温州适应性考试) 已知f(x)=x2－ax,|f(f(x))|≤2 在[1,2]上恒成立,则实数a的最大值为____.

解析这是一道填空压轴题,试题简约而不简单,若采取“强攻”,势必很快“败下阵”来.不妨先思考问题成立的必要条件,取特殊值框定a的范围,由

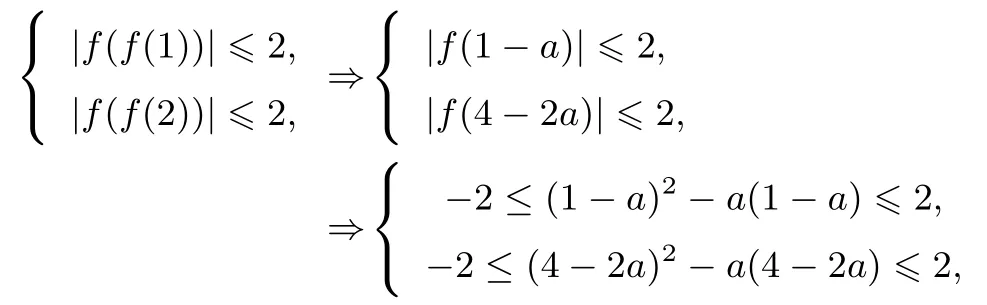
所以f(x)在[f(1),f(2)]上单调递减,而故实数a的最大值为完美解决!

例2(2018年6月浙江省数学学考) 设函数f(x)=3|ax|－(x+a)2,其中a ∈R.

(1)当a=1 时,求函数f(x)的值域;

(2)若对任意x ∈[a,a+1],恒有f(x)≥－1,求实数a的取值范围.

解析(1) 略;(2) 注意到,仅对x分类讨论,无法去绝对值,以化简f(x)的解析式.那就抓住目标,从必要条件入手,先通过特殊值来缩小所求参数的范围,为解题找到思考方向.因为对任意x ∈[a,a+1],恒有f(x)≥－1,所以

解得－1≤a≤0.

下面证明,当a ∈[－1,0],对任意x ∈[a,a+1],恒有f(x)≥－1,

①当a≤x≤0 时,

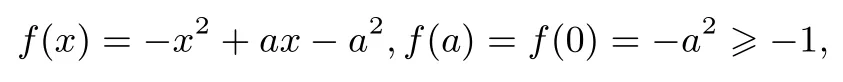
故f(x)≥min{f(a),f(0)}≥－1 成立;

②当0≤x≤a+1 时,

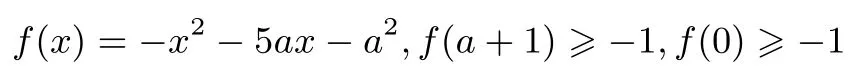
故f(x)≥min{f(a+1),f(0)}≥－1 成立.

由此,对任意x ∈[a,a+1],恒有f(x)≥－1.所以,实数a的取值范围为[－1,0].

评注特殊化是把研究对象或问题从原有范围缩小到较小范围或个别情形进行考察的思维方法,也就是说,当数学问题的一般性不十分明显时,我们可以从特殊的数、形的数量关系和位置关系入手,从而找到解题方法或构成解题起点.在解决不等式恒成立问题时,通过代入特殊值(如端点值),可以缩小所求参数的范围,甚至可以得到结果,如上述两题,但特殊化所得结论是问题成立的必要条件,接下来论证其充分性即可,这样就掌控了解题节奏,能大幅度提高成功解题的概率.

2 数形结合,借助图象直观解

例3(2018年4月浙江省数学学考) 若不等式2x2－(x－a)|x－a|－2≥0 对于任意x ∈R 恒成立,则实数a的最小值是____.

解析被一道学考试题难住了,让不少学生在数学学习上开始“怀疑人生”.令x=0,得干脆就把作为了最后结果,很可惜! 题设不等式等价于2x2－2≥(x－a)|x－a|对于任意x ∈R 恒成立,且令f(x)=2x2－2,

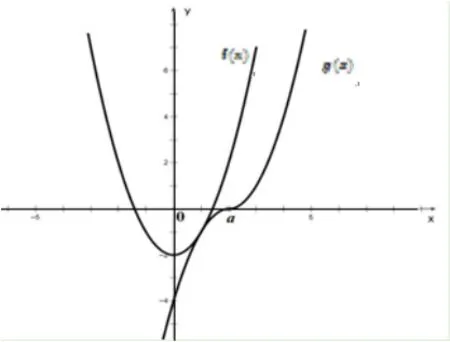
图1

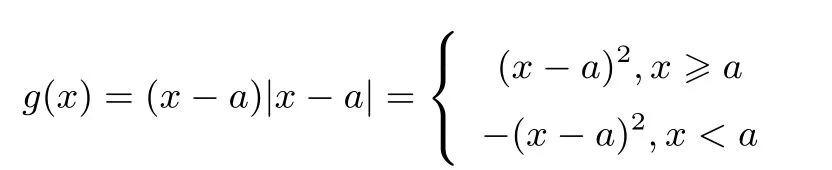
则g(x) 的图象不能在f(x) 图象的上方,在同一坐标系作出它们的图象,如图(1),可得当时,2x2－2≥－(x－a)2即3x2+2ax+a2－2≥0 恒成立,所以Δ=4a2－12(a2－2)≤0,解得综上,实数a的最小值是

例4已知函数对任意的x ∈[0,1]恒有f(x+a)≤f(x)成立,则实数a的取值范围是____.

解析是分段函数,想从“数”的角度破题无异于“与虎谋皮”,那就从“形”的角度入手,对任意的x ∈[0,1]恒有f(x+a)≤f(x)成立,就是在区间[0,1]上,f(x+a)的图象总在f(x)图象的下方或者与之重合,而f(x+a)的图象可以由f(x)的图象经过平移得到,当a=0 时,符合题意;当a＜0 时,如图(2),可得a=－1;当a＞0 时,如图(3),可得a≥1,综上所述,a≥1,a=0,a=－1.

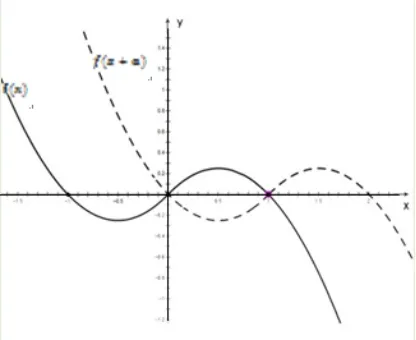
图2

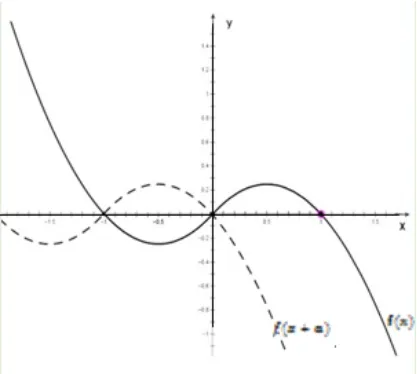
图3

3 分离参数,转化问题简洁解

例5已知f(x)=ax3,g(x)=9x2+3x－1,当x ∈[1,2]时,f(x)≥g(x)恒成立,则a的取值范围为( )

A.a≥11 B.a≤11

C.a≥D.a≤

解析f(x)≥g(x)恒成立,即ax3≥9x2+3x－1 恒成立.因为x ∈[1,2],所以对a实施分离,可得恒成立.令则当时,a≥9t+3t2－t3恒成立.令h(t)=9t+3t2－t3,则h′(t)=9+6t－3t2=－3(t－1)2+12.易知h′(t)在上是增函数,得所以h(t)在上是增函数,从而a≥h(t)max=h(1)=11.故选A,这就是分离参数法解题的“套路”.

例6若对任意的x ∈[1,4],存在实数a,当b＞0 时,使恒成立,求实数b的最大值.

解析初读本题,容易被题目复杂的信息所难住,仔细研读,分清参数与变量,思路就来了.去掉绝对值,得－2x≤x2+ax+b≤2x,注意到x ∈[1,4],分离参数a,问题等价于对任意的x ∈[1,4]恒成立,依题意,要使实数a存在,只需即可,接下来,就是求最值了.令对b分类讨论:

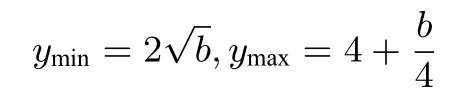
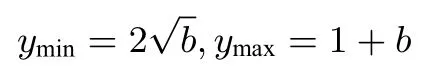
ymin=可得－(1+b)+2,解得,b ∈∅,所以b ∈∅.

综上所述,求并集得0＜b≤9,故实数b的最大值为9.

评注分离参数法通常是指对题设中含参不等式(方程)的参数进行分离,使不等号(等号)一端只含有参数(不含变量),另一端只含变量(不含参数),从而解决有关不等式恒成立、不等式或方程有解中参数的取值范围或参数最值的一种方法.对于不等式恒成立问题,如能成功分离参数,将问题转化为易于求解的函数值域或最值问题,那么就能极大地优化解题程序,使解题过程简洁明快.

4 变换主元,合理减元轻松解

例7(2017·湖州、衢州、丽水三地质检) 已知函数f(x)=ax2+bx+c(a,b,c ∈R),若存在实数a ∈[1,2],对任意x ∈[1,2],都有f(x)≤1,则7b+5c的最大值是____.

解析题目变量多,需要根据问题,分清主次.令g(a)=x2·a+bx+c,则g(a)是关于a的一次函数,在[1,2]上单调递增,得g(a)≤1 有解,于是g(a)min≤1⇒g(1)≤1,即x2+bx+c≤1 对任意x ∈[1,2]恒成立,令h(x)=x2+bx+c,则有

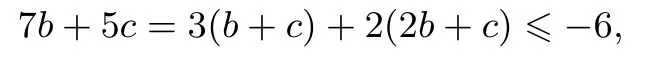
所以,当b=－3,c=3 时,7b+5c取最大值－6.

例8已知函数f(x)=lnx.若不等式mf(x)≥a+x对所有m ∈[0,1],都成立,则实数a的取值范围为____.

解析由题意得,a≤mlnx－x对所有的m ∈[0,1],x ∈都成立,令H(m)=lnx·m－x,m ∈[0,1],x ∈

所以－1≤lnx≤2,可 得即对恒成立,所以令g(x)=lnx－x则知函数g(x)在上是增函数,在[1,e2]上是减函数,所以g(x)min=g(e2=2－e2,故a≤2－e2.综上得a≤－e2.

评注在日常解题中,我们总是习惯于将多元不等式转换成x的不等式,视x为主元,这种思维定势有时会增加问题解决的难度和复杂性.像例7,例8 含多元的不等式恒成立问题,就需要紧扣问题目标,先选择某已知变量为主元,x为参数,就可以“挣脱”多元束缚,按层次有效减元消元,使问题由复杂不断走向简单,直至迎刃而解.

5 构造函数,化归最值容易解

例9当x≥0 时,不等式ln(x+1)≥x－kx2恒成立,则实数k的最小值是____.

解析当x=0 时,不等式对任意实数k恒成立,无法缩小k的范围;那就分离变量,当x＞0 时,可得恒成立,令求导后,发现导函数变得复杂,难以求g(x)的最大值,怎么办?

直接构造函数f(x)=ln(x+1)－x+kx2(x≥0),则由题意知x≥0 时,f(x)min≥0,首先f(1)=k－1+ln 2≥0,得k＞0.求导得,

(1)若2k－1＜0 即当时,有f′(x)≤0,此时＜f(0)=0,与题意不符;

(2)若2k－1≥0 即当x≥0 时,f′(x)≥0,此时恒有f(x)≥f(0)=0,符合题意,所以实数k的最小值是

例10已知函数f(x)=(x+1)lnx,

(2)存在实数k,使得对任意的实数x ∈[1,e],恒有f(x)≥(k+1)x+b成立,求k+b的最大值.

解析(1)略;(2)构造函数

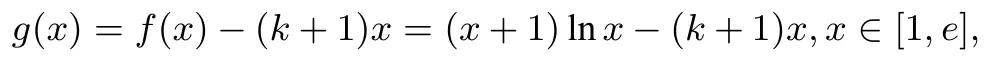
求导,得

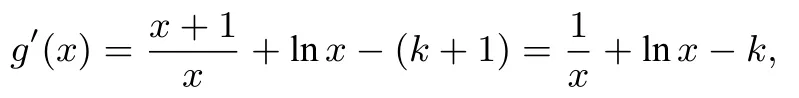
再求导,得

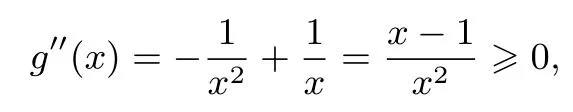
则g′(x)在[1,e]单调递增,所以

①当k≤1 时,g′(x)≥0 恒成立,知g(x)在[1,e]单调递增,则g(x)≥g(1)=－k－1,所以－k－1≥b ⇒b+k≤－1.

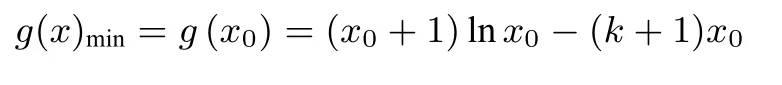
所以

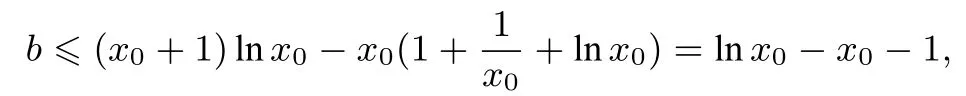
可得

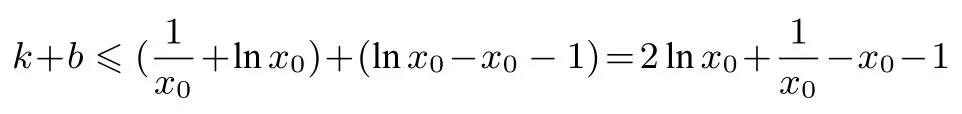
记

可得

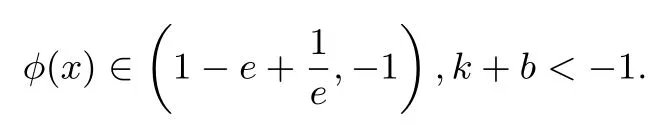
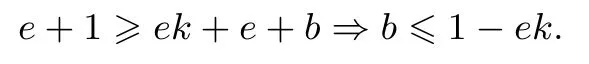
所以,

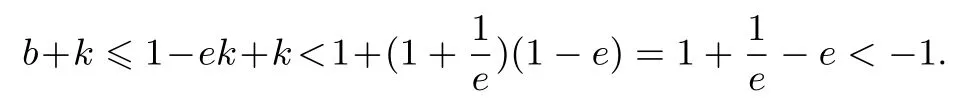
综上所述,k+b的最大值为－1.

评注函数、方程、不等式是数学中的“三驾马车”,根据解决问题的需要,在函数、方程、不等式三者之间进行适当的转化,就能把尚未解决或难以解决的问题,逐步归结为已经解决或易于解决的问题.上述两题的解法,就是通过构造函数,把不等式恒成立问题转化为函数性质研究的问题,通过讨论函数的单调性,计算函数在给定区间上的最值,从而实现问题的解决.