基于最优运输无网格法的Whipple 屏超高速撞击数值模拟*

樊 江，袁 圆，廖祜明，袁庆浩，陈高翔，黎 波

（1. 北京航空航天大学能源与动力工程学院，北京 100191；2. 凯斯西储大学机械与航空航天工程学院，美国 克利夫兰，OH44106）

太空中微流星体和空间碎片虽然体形很小，但由于通常都具有超高的相对速度（2～15 km/s），会对航天器的安全造成巨大的威胁。例如，长时间暴露的航天器外部超过30 000 个直径大于0.3 mm 的陨石坑都是由微流星体或轨道碎片撞击形成[1]。航天防护中常采用Whipple 屏对特征尺寸1 cm 以下的碎片进行破碎[2-3]。Whipple 屏在超高速撞击后的损伤状态对于Whipple 屏的优化设计至关重要。

超高速撞击的物理过程非常复杂。撞击过程中，材料的惯性、可压缩性效应或相变效应比结构效应更显著，伴随着大变形、热流固耦合、相变（液化、气化、凝固等）、碎裂等现象，采用数值方法进行准确模拟是一项巨大的挑战[4]。基于网格的超高速撞击模拟存在着网格畸变或者需要不断重新划分网格[5]的缺点；而无网格法由于不需要进行网格离散及采用高阶插值函数，有利于解决大变形和流固耦合问题，在超高速撞击问题上应用更为广泛。目前常用的无网格方法有光滑粒子流体动力学法（smoothed particle hydrodynamics, SPH）和再生核粒子法（reproducing kernel particle method, RKPM）以及质量点法（material point method, MPM）等。有大量的研究应用以上的方法[6-7]及其改进方法[8]对Whipple 屏的超高速撞击进行模拟，虽然取得了丰富研究成果，但由于算法本身的固有缺陷，仍然无法解决准确设置位移边界条件[9]、计算效率不高[10]、拉应力不稳定[11]及有效计算带摩擦的动态接触等问题，同时也缺乏严密的收敛性与误差理论分析。

最优运输无网格方法（optimal transportation meshfree, OTM）是由Li 等[12]提出的一种基于最优运输理论和局部最大熵插值函数的无网格方法，该方法结合基于能量释放率的物质点失效方式，能够很好地解决现有Whipple 屏超高速撞击模拟方法存在的问题。

本文首先采用OTM 法模拟铝球超高速撞击单层铝板，通过与实验结果以及其他数值方法的计算结果的比较，验证OTM 法在超高速撞击问题上的适用性；然后采用OTM 法对Whipple 屏超高速撞击问题进行模拟，研究不同速度不同撞击角度下的碎片云形状、缓冲墙弹孔尺寸以及后墙剥落穿透的损伤情况，并与文献[13]的实验结果进行对比。

1 OTM 理论

OTM 法的主要特点是采用局部最大熵无网格插值函数，克服了一般无网格法中插值函数不满足Kronecker delta 属性的本质缺陷，解决了传统无网格法难以准确施加位移边界条件的问题；采用物质点充当积分点，有效避免了计算结果在拉伸载荷下的不稳定性；采用最优运输理论对时间离散，保证了哈密顿作用量的时间离散形式满足动量守恒条件，且收敛性能得到严格的数学证明[14]；采用基于能量释放率的物质点失效方式，能够很好地模拟材料的损伤情况，并且该方式已被证明可收敛到 Griffith 断裂准则[15]。

1.1 时间离散

1.2 空间离散

OTM 法将计算域分为两类点的集合。一类为节点，用下标a 表示，包含了位置、速度、加速度的信息；一类为物质点，用下标p 表示，包含了材料参数、质量、应力应变等信息，相当于一般有限元法中的积分点。定义在时刻节点的坐标为，物质点的坐标为如图1 所示。

图1 空间离散示意图[17]Fig. 1 Spatial discrete diagram[17]

1.3 失效准则

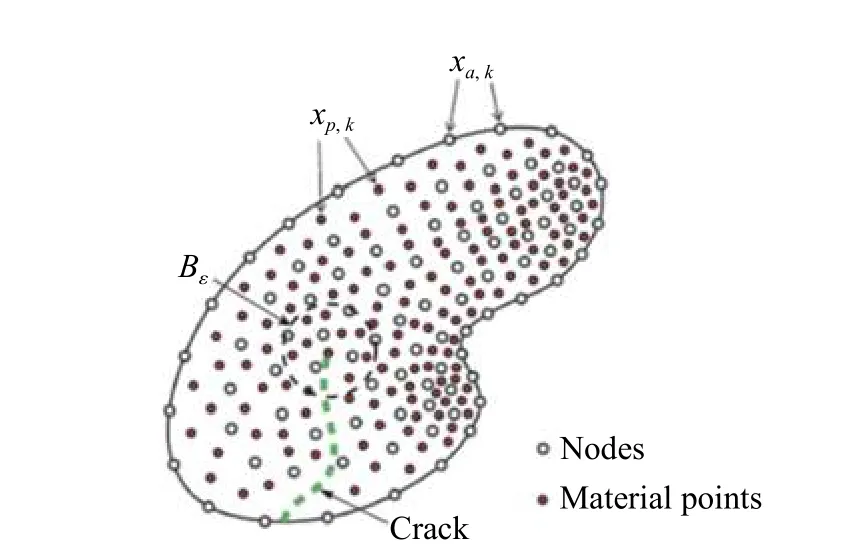
图2 评估能量释放率的局部邻域[15]Fig. 2 The local neighborhood used to estimate the energy-release rate[15]

2 铝球超高速撞击铝板算例分析

文献[8]采用基于拟流体模型的SPH 新方法（拟流体SPH 法）对铝球超高速撞击铝板进行了数值模拟，并与Hiermaier 等的实验结果、传统SPH 法和自适应光滑粒子流体动力学法（adaptive smoothed particle hydrodynamics, ASPH）的计算结果进行了对比。本节将采用OTM 法对相同的算例进行模拟，并与文献[8]中的结果进行比较。

图3 铝球撞击铝板离散模型Fig. 3 Discrete model of aluminum ball impacting single aluminum plate

2.1 数值模拟模型

2.2 材料模型

超高速撞击需要考虑弹丸和靶材的应变率硬化和热软化等问题，因此选择能较好地模拟铝合金材料塑性响应的J2 粘塑性模型（J2-viscoplasticity）。

J2 粘塑性模型有效屈服应力为

式中：J=V/V0，V 为当前体积，V0为初始体积；为参考熔化温度；为参考体积下的Grüneisen 参数，为常数。铝合金型号为LY12，材料参数如表1 所示。本算例中依据文献[8]提供的材料信息进行了部分参数修改。式(15)和式(16)中提到的各参考系数的取值如表2 所示。高温高压下材料的变形与温度、压力的关系采用SESAME 状态数据库描述[18]。

表1 LY12 材料参数Table 1 Material parameters of LY12

表2 J2 黏塑性模型参数Table 2 Parameters of J2 viscoplasticity model

2.3 结果分析

OTM 法能够很好地模拟内核碎片云的位置、外泡碎片云的形态以及反溅碎片云的形态等特征信息。特别是反溅碎片云的膨胀距离和宽度，与实验很好吻合。一般的SPH 法由于采用Johnson-Cook 损伤模型而导致薄板屈服应力小于真实的屈服应力，外溅碎片云的反溅程度过大，与实验偏差较大（如图4 所示）。

图4 OTM 法与各类SPH 方法计算结果对比Fig. 4 Comparison of OTM and various SPH methods’ simulation results

表3 铝球超高速撞击铝板结果对比Table 3 Comparison of high-velocity impact results between aluminum projectile and plate

3 Whipple 屏超高速撞击模拟

3.1 对比实验简介

文献[13]进行了一系列Whipple 屏超高速撞击实验（如图5 所示），球形弹丸直径0.4～0.5 cm，撞击速度4.47～6.15 km/s，撞击角度分为0°和45°两种。靶材间距为10 cm，厚度为0.192 cm。实验得到不同撞击速度和撞击角度下的弹孔尺寸、后墙损伤情况和碎片云激光阴影照片等结果。

3.2 数值模拟模型

本文按照对比实验建立模型，模拟了撞击角度为0°和45°两种情况。在划分网格时细化了缓冲墙和后墙的中心区域，最小网格尺寸为0.2 mm。在正撞模拟中，物质点共有340 382 个，节点共有67 389 个（如图6 所示）；在斜撞模拟中，物质点共有340 473 个，节点共有67 401 个。

弹丸和靶材的材料型号均为LY12，材料模型仍然使用J2 粘塑性模型（材料参数见表1、表2）和SESAME 状态方程。

3.3 结果分析

文献[13]进行了一系列不同撞击速度的Whipple 屏正撞与斜撞实验。参数设置如表4 所示。

OTM 法采用相同的参数进行对应的数值模拟，实验与仿真中的缓冲墙弹孔尺寸对比结果如表5 所示。其中后四组是斜撞实验，得到的弹孔呈现椭圆形，弹孔尺寸指的是椭圆的长轴和短轴。

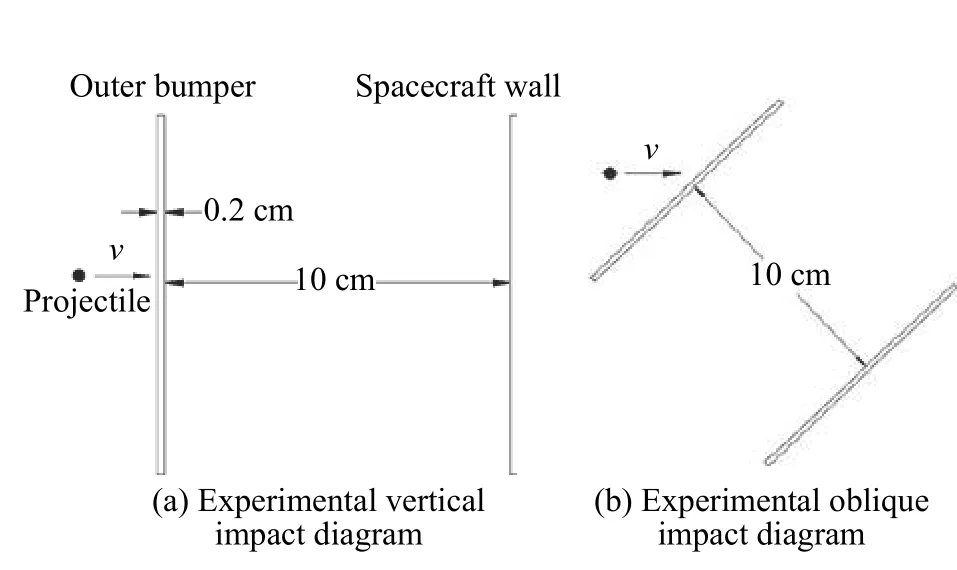
图5 实验模型示意图Fig. 5 Schematic diagram of experimental model

图6 Whipple 屏超高速撞击数值模拟模型Fig. 6 The numerical simulation model of Whipple shield hypervelocity impact

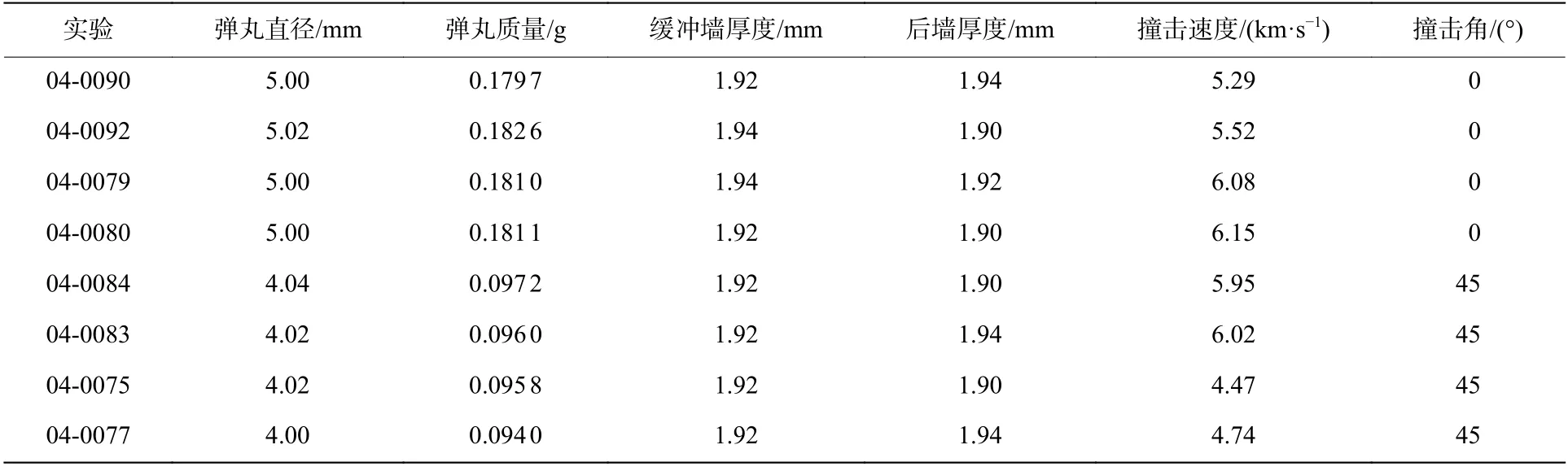
表4 实验参数设置Table 4 Parameters in experiments

表5 缓冲墙弹孔尺寸对比Table 5 Bullethole size comparison of outer bumper

缓冲墙弹孔尺寸的模拟结果与实验吻合得较好，如在撞击速度5.29 km/s 的实验中，弹孔直径为1.15 cm，而仿真的结果为1.05 cm，相对误差为8.69%（如图7 所示）。

图7 缓冲墙损伤对比图(撞击速度5.29 km/s)Fig. 7 Damage characteristics comparison chart of outer bumper (Impact velocity 5.29 km/s)

后墙的损伤形式一般有成坑、产生鼓包、层裂、剥落和穿孔[19]。文献[13]只关注剥落和穿透，如图8(a)所示。图8(b)为OTM 仿真中的剥落和穿透。

对比仿真与实验中后墙损伤情况（如表6 所示），可见正撞仿真中，撞击速度越大，后墙的损伤越小。这是由于速度大的弹丸被缓冲墙破碎得更充分，形成了更小的碎片，减轻了对后墙的破坏作用。这与文献[13]中的结论一致。

图8 实验与仿真中的剥落和穿透Fig. 8 Definitions of spalling and penetration in experiments and simulations

表6 后墙损伤情况对比Table 6 Damagecomparison of spacecraft wall

仿真显示，弹丸碎片撞击到后墙上，残余应力约为150 MPa，而撞击较严重的区域残余应力达到300 MPa 以上，如图9 所示。

图9 后墙损伤图(撞击速度5.29 km/s)Fig. 9 Damage characteristics of spacecraft wall (impact velocity is 5.29 km/s)

目前超高速弹丸与Whipple 防护屏撞击的数值模拟，很难精确模拟出后墙的损伤情况。大部分后墙的损伤数据都来自于实验。文献[8]用拟流体SPH 法对Whipple 屏撞击的研究中，也只给出了后墙的中心损伤区域，缺乏对于后墙剥落与穿透等损伤状态的探究。由此可看出，OTM 法基于能量释放率的物质点失效的方式，在模拟材料的断裂损伤方面有着明显的优势。

OTM 法对Whipple 屏的超高速撞击模拟不仅能模拟出弹丸穿透缓冲墙形成碎片这一过程，还能很好地模拟出碎片云的形态，包括碎片云呈现出头部椭圆形、尾迹扇形并有扩散趋势、碎片大多集中在头部和缓冲墙穿孔处等细节特征，如图10～11 所示。由于实验中的碎片云照片是采用激光阴影技术得到的，细微的碎片无法在照片中显示，因而实验中的碎片云轮廓较为清晰；而OTM 计算得到的碎片云对比图中，所有碎片均有显示，轮廓有一定发散性。

图10 正撞碎片云对比图Fig. 10 Fragment cloud comparison chart of vertical impact

图11 斜撞碎片云对比图Fig. 11 Fragment cloud comparison chart of oblique impact

4 结 论

本文采用OTM 法对铝球超高速撞击铝板和Whipple 防护屏超高速撞击进行了数值模拟。通过铝球超高速撞击铝板这一验证算例，可看出OTM 法能够为超高速撞击问题提供有效的数值模拟手段。在Whipple 屏的超高速撞击模拟中，OTM 法能够很好地预测Whipple 防护屏与弹丸撞击时缓冲墙和后墙的损伤情况，尤其在模拟后墙的剥落、穿透等损伤状态和破碎过程中碎片云的形态变化方面有着显著的优势，验证了其在超高速撞击数值模拟方面的适用性，为Whipple 防护屏在航天防护方面的相关探究提供了有效的数值模拟手段。