Zr 基非晶合金JH-2 模型的构建及应用*

张云峰，罗兴柏，刘国庆，施冬梅

（陆军工程大学石家庄校区，河北 石家庄 050000）

Zr 基非晶合金具有高强度、高硬度、高弹性极限等优异力学性能，当该材料受到动态冲击载荷后，温度升高并破碎生成碎片云，碎片云与空气中的氧气发生燃烧反应释放大量内能，因此，该材料是一种较理想的新型反应金属材料[1-2]。在国防领域，学者们对Zr 基非晶合金作为长杆侵彻体[3-4]、聚能装药药型罩[5-6]、预制破片[7-8]、复合装甲[9]等毁伤、防护元素开展了大量研究，取得了较丰硕的成果，证明该材料在军事应用中具有光明前景。

战场环境下，毁伤与防护元素间通常存在高速撞击的相互作用，材料受到高速撞击而处于高压、大应变、高应变率状态。通过弹道实验研究材料极端状态下的损伤、失效、贯穿等特性成本高昂，且受实验技术限制，很多物理量及作用过程无法直接测定。流体动力学模拟不受上述因素制约，极大提高了毁伤与防护元素的设计、分析效率[10]，描述材料动态力学特性的材料模型不可或缺。目前，针对动载荷下Zr 基非晶合金材料模型的研究成果较少，且均简化了模型构建方法，材料模型的适用性不强，随着该材料在国防领域的广泛应用，构建动载荷下Zr 基非晶合金的材料模型十分必要。

Zr 基非晶合金受压缩破坏前几乎没有宏观塑性应变，压缩强度略大于拉伸强度，属典型脆性材料。Holmquist 等提出了适用于玻璃、陶瓷等脆性材料的Johnson-Holmquist 分段模型（JH-1 模型）[11]和Johnson-Holmquist 本构模型（JH-2 模型）[12]，并确定了聚苯乙烯泡沫[13]、B4C[14-15]、AlN[16]、SiC-B[17]等材料的模型参数，这些模型及参数被广泛应用于流体动力学模拟中且被证明行之有效。对于Zr 基非晶合金，Ma 等[18]、Wang 等[19]的研究证明了其软化、损伤行为的连续性，材料强度线性分段的JH-1 模型显然不适用，因此本文中关注材料JH-2 模型的建立和应用。在JH-2 模型的构建及应用方面：Wang 等[20]构建了岩石的JH-2 模型，并将之运用于隧道光面爆破的数值模拟和实验分析；Simons 等[21]以氧化铝陶瓷的JH-2模型为基础，通过数值模拟研究了材料的高压动态响应；张云峰等[22]通过初步构建的JH-2 模型，研究了Zr 基非晶合金的剪切释能特性；王枫等[23]依据材料的JH-2 模型，通过数值模拟研究了球状混凝土对房屋瓦片的破坏，为防灾减灾研究提供了依据。

受目前实验技术的限制，并非所有的材料模型参数都能在实验室环境中直接确定，部分参数需要通过弹道实验“反馈”间接确定，并与成分、特性相近材料对比验证[13-17]。本文的研究对象为Zr62.5Nb3Cu14.5Ni14Al6非晶合金，石永相[24]通过平板冲击实验给出了该材料的高压响应，并测试了不同应变率下该材料的轴向压缩强度。Togo 等[25]、Martin 等[26]研究了性能相近的Zr55Al10Ni5Cu30、Zr57Nb5Cu15.4Ni12.6Al10非晶合金的冲击高压响应。Wang[27]综述了Zr 基非晶合金的基础力学性能，探讨了非晶合金的弹性与温度、压力等的内在联系。

本文中简述了JH-2 模型，确定了Zr62.5Nb3Cu14.5Ni14Al6非晶合金的模型参数，并以材料模型为基础，对比了平板冲击与破片侵彻的实验结果和数值模拟结果，检验了材料模型的准确性和适用性。

1 JH-2 模型

图1 JH-2 模型[12]Fig. 1 Description of the JH-2 model[12]

2 参数确定

2.1 压力

JH-2 模型的压力部分为材料所受静水压力，目前没有公开发表的Zr62.5Nb3Cu14.5Ni14Al6非晶合金静水压力-体应变关系的实验数据，因此，采用平板冲击实验数据计算材料静水压力。非晶合金动态载荷下失效前根据冲击雨贡纽曲线与静水压力-体应变曲线间的关系，当击波方向上应力大于HEL 时，静水压力与冲击正应力间的关系为[10]：

图2 为材料的压力-体应变关系，图中实线为确定的压力模型，三角形点为平板冲击实验数据，菱形点为根据实验数据和式（17）计算的静水压力，由平板冲击实验中正应力与静水压力的关系，正应力位于静水压力上方，材料模型与静水压力数据走势基本吻合。需要注意的是，Zr 基非晶合金在平板冲击压力30～40 GPa 下发生相变[25-26,31]，导致p-µ曲线斜率减小，可据此计算出该压力模型的应用范围。由简单冲击动力学计算得到，Zr62.5Nb3Cu14.5Ni14Al6非晶合金破片以1 500 m/s 的速度冲击钢板、以2 200 m/s 的速度冲击铝板时对应的压力约为30 GPa，因此，确定的力学模型参数可以满足大多数兵器速度范围内的数值模拟研究与应用。

图2 材料的压力-体应变关系Fig. 2 Relation between pressure and volumetric strain for the material

2.2 损伤

图3 确定的材料归一化静水压力-等效破碎应变关系Fig. 3 Determined relation between normalized hydrostatic pressure and equivalent crushing strain for the material

表1 平板冲击实验数据[24] 及相应计算结果Table 1 Experimental data[24] by plate impact tests and the corresponding calculation results

2.3 强度

雨贡纽弹性极限为材料在一维正冲击波加载下达到弹性极限时的压缩应力，该应力包含压力和强度分量。在雨贡纽弹性极限处，式（20）可写作：

图4 材料的应变率敏感性Fig. 4 Strain rate sensitivity of the material

拟合约束条件为模型需通过σH（对应应变率105.05s−1），最终得到A=0.83，N=0.34。拟合材料模型参数A、N、C 的过程中所使用的轴向压缩实验数据如表2 所示。

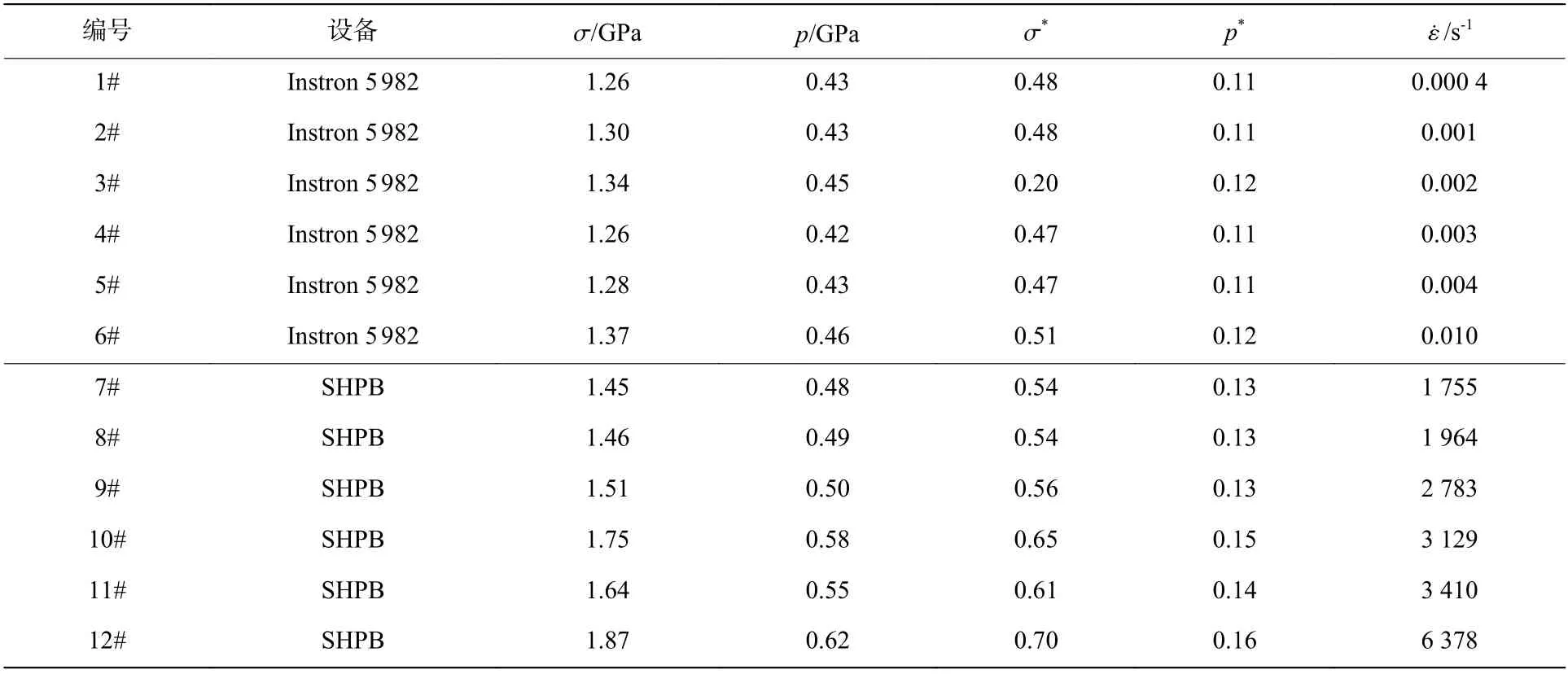
表2 Zr62.5Nb3Cu14.5Ni14Al6 非晶合金轴向压缩实验数据[24]Table 2 Experimental data of axial compression for Zr62.5Nb3Cu14.5Ni14Al6 amorphous alloy[24]

实验室条件下，破碎材料强度的测试较困难，一般需根据弹道实验数据，采用“反馈法”间接确定破碎材料的强度参数B、M，步骤如下：给出一组B、M 值，并根据式（25）拟合出对应的D1、D2，对比采用该组模型参数的数值模拟结果与实验结果；不断调整材料参数，直至数值模拟结果与实验结果间误差最小。数值模拟利用平板冲击实验v=350，390 m/s 两组自由面粒子速度作为基准数据，具体的数值模拟布置在第3 节给出。

依据一般脆性材料特性，B、M∈（0，1）。首先令M=0.5，B 在（0，1）范围内变化，发现：当B≤0.3 时，误差随着B 的增大而减小；当B＞0.3 时，误差随着B 的减小而增大。令B=0.3，M 在（0，1）范围内变化，发现：当M≤0.2 时，误差随着M 的增大而减小；当M＞0.3 时，误差随着M 的减小而增大；M 取0.2、0.3 时，误差近似相等，约为3.8%。因此，取B=0.3，M=0.25。表3 为计算参数与对应的误差，该误差为实验与数值模拟得到的自由面粒子速度曲线平台段对应点误差的平方平均数。

表3 计算参数及误差Table 3 Parameters and errors

图5 构建的无损材料强度模型和破碎材料强度模型Fig. 5 The intact strength and fractured strength models developed for the material

3 数值模拟

材料JH-2 模型的构建过程既包括对实验结果的直接拟合，也包括基于弹道实验数据的反馈法，因此，模型参数不可能绝对精确，需要进行数值模拟结果与实验结果的对比检验，数值模拟过程中使用的材料参数如表4 所示。

表4 Zr62.5Nb3Cu14.5Ni14Al6 非晶合金材料常数Table 4 Parameters of the JH-2 model for Zr62.5Nb3Cu14.5Ni14Al6 amorphous alloy

3.1 平板冲击

图6 为平板冲击数值模拟结果与实验结果的对比，直径为110 mm、厚度为5 mm 的铜质飞片分别以350、390、439、502、550 m/s 的速度冲击直径为20 mm、厚度为4 mm 的Zr62.5Nb3Cu14.5Ni14Al6非晶合金试样，测试数据为试样自由面速度，实验布置详见文献[31]。采用Autodyn 3D 软件模拟平板冲击实验过程，材料几何模型用Lagrange 法建立，网格尺寸为0.2 mm；铜制飞片的材料模型分别为冲击物态方程、Steinberg-Guinan 本构关系，其材料参数见表5。350、390 m/s 两组实验验数据用来确定材料参数B 和M，439、502、550 m/s 三组实验数据用来验证模型的准确性。

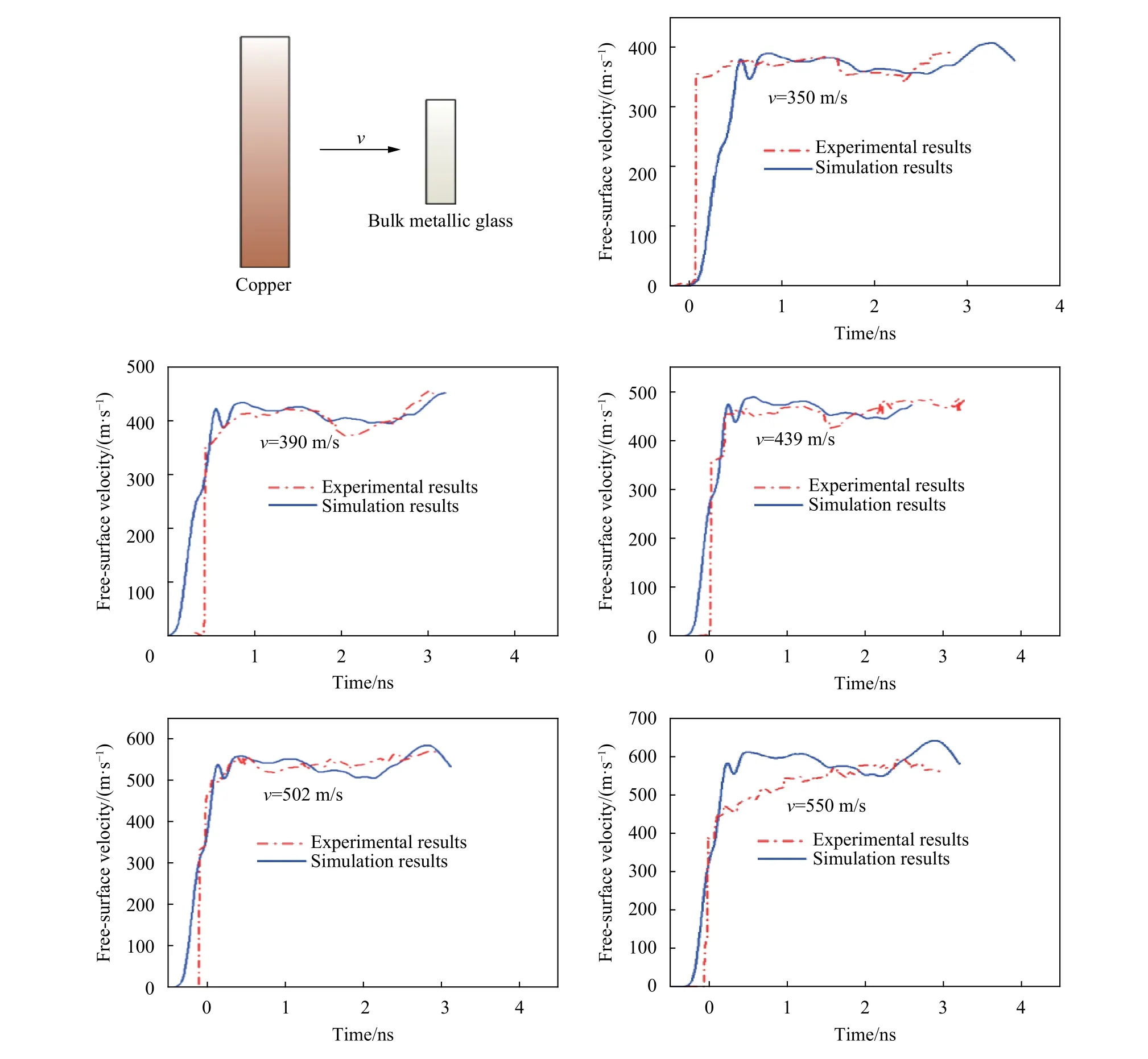
图6 不同冲击速度下，试样自由面速度的数值模拟结果与平板冲击实验结果的对比Fig. 6 Comparison of simulated impact-induced free-surface velocities in samples with those measured in flyer-plate impact tests at different impact velocities

表5 数值模拟中铜材料参数Table 5 The parameters of copper in the simulations

图6 中曲线上升阶段，弹性波先到达材料自由面，而后塑性波赶上弹性波：实验结果表现为自由面速度曲线迅速跃升至HEL 处后，再缓慢上升至最高点，形成平台，而JH-2 模型无法精确表达材料弹塑性波的传播过程[14-16]，数值模拟结果表现为曲线较缓慢的上升。当曲线升至最高点后，数值模拟与实验结果中平台数值间的误差分别为2.1%、3.9%、4.3%、2.8%和9.8%，走势总体上较吻合。实验过程中，材料制备、试样加工、实验布置都对实验结果有一定影响。v=550 m/s 下的实验数据曲线形态与其他曲线存在明显差别，实验结果存在较大误差，该误差在图3 损伤数据中也较明显。但总体上，数值模拟结果较好地表现了冲击载荷下的材料力学性能。

3.2 破片侵彻

Zr 基非晶合金破片撞击靶板的过程中包含材料的损伤、破碎行为，能较完整地检验材料模型的精确性。该部分计算没有用于拟合材料模型常数，可独立验证模型及常数的准确性。图7为侵彻实验布置概略及实验现场布置，直径为8 mm、长度为10 mm 的圆柱型破片由口径为14.5 mm 的弹道枪发射，撞击30 mm 厚的45 钢靶，破片速度由断通靶及计时仪测量，记录破片的侵彻深度、开坑孔径。数值模拟计算中，采用二维光滑粒子流体动力(smoothed particle hydrodynamics，SPH)法以更好模拟脆性材料的真实状态，粒子设置为尺寸为0.2 mm。靶板采用二维拉格朗日算法构建，网格为边长0.2 mm的正方形网格。钢靶材料模型为线性物态方程和Johnson-Cook 强度和断裂模型[28]，材料参数见表6。

图7 侵彻实验装置的布局Fig. 7 Layout of devices for penetration tests

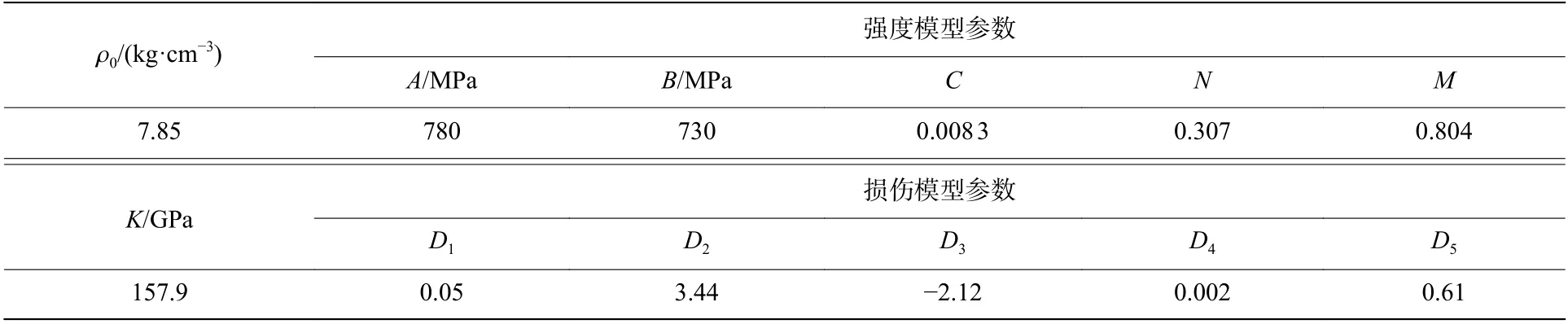
表6 数值模拟中45 钢的材料参数Table 6 The parameters of 45 steel in the simulations

实验中，测得破片撞击速度分别为692.5、938、1107.5、1 173.5、1 356.5 m/s。图8 为靶板横截面的数值模拟结果与侵彻实验结果的对比。数值模拟中靶板上弹坑的形状与实验结果极其相似。由于Zr 基非晶合金为脆性材料，破片撞击靶板后其头部首先破碎，破片边缘碎片向四周移动，破片逐渐变形为接近半球形，靶板上形成半球状弹坑。半球状侵彻体的中部质量较集中，侵彻深度最大，而边缘部分侵彻深度较小。靶板材料被破片推向弹坑周围，在弹坑边缘形成了卷边。图9 为破片对靶板的侵彻深度和开坑孔径的数值模拟结果与侵彻实验结果的对比，数值模拟结果与实验结果展现了较好的一致性。随着撞击速度的升高，弹坑内残余破片碎片对侵彻深度测量的影响减弱，数值模拟结果与实验结果更接近。

需要注意的是，Zr 基非晶合金破片侵彻钢靶的实验过程中发生了剧烈的氧化反应，该反应的反应条件为高温破片碎片飞散后与空气中的氧气充分混合，其对侵彻过程影响极小，因此在数值模拟过程中未作考虑。

图8 靶板横截面的数值模拟结果与侵彻实验结果的对比Fig. 8 Comparison of cross sections of targets between numerical simulation and penetration test results

图9 不同冲击速度下的侵彻深度和弹坑直径Fig. 9 Penetration depths and crater diameters at different impact velocities

4 结 论

构建了Zr62.5Nb3Cu14.5Ni14Al6非晶合金的JH-2 模型，其中压力-应变参数、无损材料强度参数及损伤参数根据实验数据直接确定，破碎材料强度参数通过数值模拟结果与实验结果对比的反馈法间接确定。通过数值模拟结果与实验结果的对比验证了材料模型的准确性，平板冲击数值模拟得到的材料自由面速度曲线与实验结果基本吻合；破片侵彻数值模拟中的侵彻深度、开坑孔径情况与实验结果一致性较好，模型准确地反映了材料的力学响应，使用一组模型参数的数值模拟结果能较好地匹配大范围内实验数据。由于部分参数是通过数值模拟与实验结果对比反馈得出，这些参数带来了部分不确定性，同时JH-2 模型在真实反映材料响应方面还有待进一步改进。