动态规划算法的三式融合教学法案例研究
2020-08-10吴清寿郭磊
吴清寿,郭磊
(武夷学院数学与计算机学院,武夷山 354300)
1 问题概述
《算法设计与分析》课程是计算机相关专业的核心课程,教学过程涉及算法基本思想的理解、算法的设计模式、算法的特性和算法的效率等环节,关联的前导课程较多,要求学生具备较好的基础知识和较强的分析能力。而与课程地位相悖的却是课时的大量压缩,现在各高校对本课程的课时安排一般都少于40节[1],笔者所在学校对本课程的课时安排是32+8,即32节理论讲解加上8课时的上机实践。课时量不足与课程内容较高的复杂度两者之间的不均衡给教学造成了困难:知识点抽象层次较高,囿于课时无法深入分析;需要大量的实践巩固对算法思想的理解,但实践课时通常很少甚至没有;学生普遍缺乏将理论内化为编程思想的能力。
动态规划法是《算法设计与分析》课程的重要章节,也是历届学生普遍反映较难理解的内容。本章节内容除了具有课程本身的教学难处之外,其教学难点还体现在以下几个方面:一是对算法的最优子结构性质理解存在困难。不同问题,其最优子结构性质的证明方法都不同,这是学习算法过程中的主要障碍。二是对算法的运行过程难以理解。动态规划算法通常以递归的方式定义其子问题的最优解,而递归方法在思想上易于理解,但其执行过程的分析存在较大的难度。三是无法做到学以致用[2]。学生可以通过课堂学习掌握相关例子的求解方法,但针对新的问题难以提出有效的算法过程。究其原因,主要是对算法的思想理解不透彻,对算法解决具体问题的过程掌握不清楚造成的。
文献[3]从培养学生算法思维和提高应用能力的角度提出了教学改革措施。文献[4]从多个实例中抽象出动态规划算法的特征。文献[5]用改进的动态规划算法解决了背包问题。上述文献从不同的角度对动态规划算法进行了研究,但未对学生如何更好掌握算法提出解决方法。
结合学生的实际情况,提出一种合理有效的教学方法,对学生掌握动态规划算法的基本思想、基本性质及其在具体问题上的分析方法是一件有必要有意义的工作。为此,笔者在多年教学《算法设计与分析》课程的过程中,提出了一种“三式融合”的教学模式,旨在促进学生把握问题本质,理解算法思想,提升实践能力,做到学以致用。
2 三式融合教学法
要掌握动态规划算法,首先要掌握其基本思想[6]。将原问题分解为相应的子问题是分治法和动态规划法的共同思路,而子问题是重复的还是相互独立的决定了算法的选择问题。为了便于后续更大规模问题的求解,动态规划法通过引入填表法(或者称备忘录)记录每个子问题的最优解。先从极小的(即可直接求解的)子问题开始,将其解填充到备忘录。逐步扩大问题规模,当前问题与子问题性质相同,可通过查子问题的解构造当前问题的解,提高了算法效率,避免了子问题的重复求解过程。
从上述基本思想中可以看出,适用于动态规划法求解的问题通常具有重复子问题性质和最优子结构性质。利用重复子问题性质,解决了冗余计算问题,而最优子结构性质确保问题求解的每一步骤都包含了子问题的最优解。
基于以上基本思想,以0-1背包问题的求解过程为例,采用三式融合方法,给出问题求解步骤,推导出问题的递归关系式,将求解过程图表化,从而自然得到算法的实现代码。
三式融合教学法包含公式归纳,表格填充和代码编写三个部分。下面对三种方法予以介绍,并在下一章中结合具体的案例进行分析。
(1)公式是本质。动态规划法中,利用重复子问题性质和最优子结构性质可以定义解的递归公式,但解决一个新问题的递归公式的提出并不是显而易见的,需要通过对问题进行具体的分析之后再予以总结归纳而得出。
(2)图表是手段。公式刻画了问题的本质,但求解过程仍然是抽象的。通过图表的形式将求解过程具象化,能够加深学生对问题的理解,获得对问题的形象认知,进而对新问题能够举一反三,达到掌握算法的求解方法及本质特征的效果。
(3)代码是目的。算法的理解是前提条件,但最终还需将其转化为程序代码,获得从分析问题到解决问题的能力,这是提出三式融合教学法的主要目的。利用公式抽象问题的本质,利用图表表征公式的求解步骤,依据表格的填充过程及方法,模拟出程序代码,大大降低了程序设计的难度,且程序执行结果易于验证,让学生从中获得编程的乐趣,并系统掌握程序设计的方法。
在实际教学过程中,三者不是独立的,而是根据问题的特征,将三种方法交替使用,有机融合,让学生在逐步分析问题的过程中掌握算法。
3 实例分析
本文以动态规划解0-1背包问题为例。
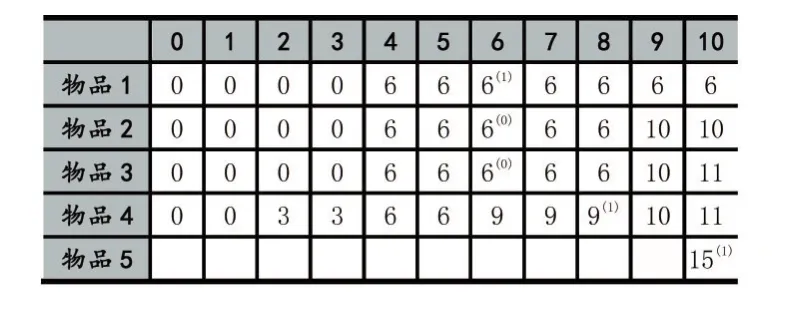
案例数据:n=5,C=10,w={4,5,6,2,2},v={6,4,5,3,6},表示有5个物品,w表示第i个物品的重量,vi表示第i个物品的价值,1<=i<=5,C表示背包的容量。这是一个0-1背包问题,物品不能分割后装入背包,只能选择整个放入或不放入。目标:要求装入背包中的物品的总价值最大。
为了填充表格,先设一个二维数组m[i][j],i(1<=i<=5)表示第i个物品,j(0<=j<=10)表示背包的当前容量,m[i][j]表示当背包容量为j时装入前i个物品产生的最大价值。
步骤一:首先考虑当背包的容量为0时,此时无法装入任何物品,则产生的价值为0,可以得到公式(1):

填充结果见表1中的第0列。
可用代码描述如下:
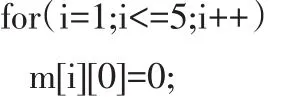
步骤二:考虑第一个物品的装入问题,设背包的容量为c,当c小于w1,此时物品不能放入背包,产生的价值为0,从而得到公式(2):

表格填充情况见表1中的m[1][1]~m[1][3]。
可用代码描述如下:
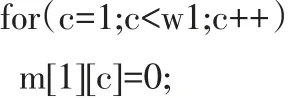
当背包容量等于或大于w1时,物品可以放入背包,则产生的价值为v1。因为当前只有一个物品,背包中物品的最大价值为v1。得到公式(3):

表格填充情况见表1中的m[1][4]~m[1][10]。
对应代码如下:
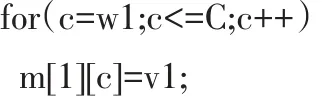
步骤三:现在考虑有两个物品的情况,当背包剩余容量c 表格填充情况见表1中的m[2][1]~m[2][4]。 对应代码如下: 当背包容量c>=w2时,第二个物品可以放入背包,也可以不放入,这需要根据是否能产生当前最优价值来决定。若物品2放入,产生价值v2,其对应的背包总价值应当为前一步骤中未放入w2前对应的背包(其容量为c-w2)中物品的总价值与v2之和,即m[i-1][cw2]+v2。若物品2不放入,则当前的总价值为步骤二中对应的背包(其容量为c)中物品价值的最优值m[1][c],取两者最大值作为当前容量下背包中的最大价值。由此,得到公式(5): 表格填充情况见表1中的m[2][5]~m[2][10]。 对应代码如下: 以m[2][8]的填充为例。当背包容量为8时,背包容量小于前两个物品的重量之和,则只能选择一个,第一个物品的价值大于第二个物品价值,所以选择将第一个物品装入背包,背包中的物品价值为6。其实际计算过程是m[1][c-w2]+v2=m[1][8-5]+v2=m[1][3]+4=0+4=4,可以看出,m[1][3]处未产生价值,即未装入物品1,所以此处只装入物品2。m[1][c]=m[1][8]=6,表示装入物品1,产生价值为6,所以应选择6作为当前背包的物品总价值。 步骤四:当n>i>2时,其计算过程与步骤2相同,可得到通用公式: 表格填充情况见表1中的第3第4行。 代码与步骤三相似,此处略。 步骤五:当i=n时,因为m[i][c]的值只与m[i-1][c]的值相关,所以此时无需完整计算整个过程,只需根据公式(7)计算c=C时的m[n][C]即可。 则 m[n][C]=max(15,11)=15 由上述步骤得到的完整表格如表1所示。 表1 0-1背包问题各步骤最优值 由最优值构建最优解的过程较为简单,从m[n][C]开始搜索,如果m[i][c]>m[i-1][c],说明在容量为c时,对于第i个物品,将其放入背包中将得到当前的最优解,则令xi=1,并缩小背包容量为c-wi,继续对i-1个物品的放入情况即m[i-1][c-wi]进行检查,构造最优解。如果m[i][c]==m[i-1][c],说明放入第i个物品无法产生新的更优的解,则第i个物品不构成最优解,令xi=0,并由m[i-1][c]继续构造最优解。重复以上过程。当i等于1时,考虑构建最优值的步骤二中m[1][c]只有两种取值:0 和 v1,所以,只要判断 m[1][c]>0,则 x1=1,否则x1=0。表 1 中的 m[5][10],m[4][8],m[3][6],m[2][6],m[1][6]为最优解的求解顺序,其单元格右上角括号中的值即为 xi的值,可以看出 x={1,0,0,1,1},即选择物品 1,4,5,背包中的物品价值最大。 从近几年的教学情况可以看到,通过三式融合的教学方法,可以有效地帮助学生理解算法的基本思想,全面掌握算法的执行情况,并能较容易的将分析过程转化为程序代码,提升了学生的实践动手能力。另外,学生可以通过这种方法对比用不同算法解决同一问题的优缺点,进而提出算法的改进措施,并能将其应用到新的问题上。
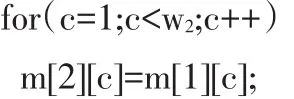
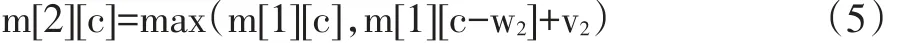
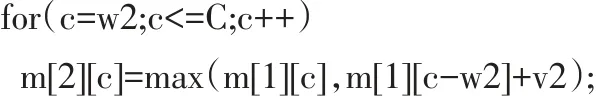
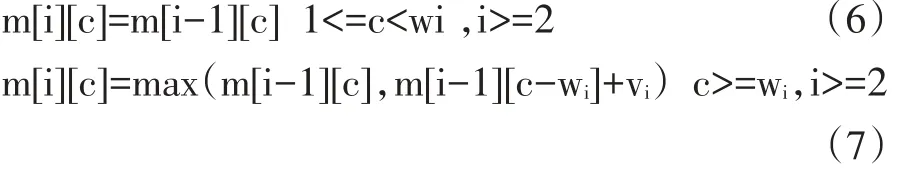
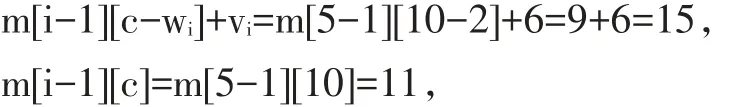
4 结语
