从作线段的中点看学生思维的发展

郭梅梅?胡赵云

一、问题提出

七年级数学会讲尺规基本作图，也会讲线段的中点的概念，但一般不讲尺规作图“作线段的中点”，通常在八年级学习“线段垂直平分线”及其作图时顺便介绍。无论是“作线段的中点”，还是“作线段的垂直平分线”，教科书都会给出作法：

1.分别以点A、B为圆心，大于AB长为半径作弧，两弧分别交于点C和点D;

2.连接CD交AB于点O;

则点O就是线段AB的中点。

那么问题来了，“大于AB长为半径”这句话是谁最先想出来的？学生自己能想出来吗？怎样帮助学生想出这个作图方法？在六年级（上海学校实行五四制）教“作线段的中点”，该如何教才能有益于学生思维发展？

二、认知基础简析

先思考与“作线段的中点”有关的几个问题：（1）学生的认知起点是什么？（2）设置什么问题或提供什么情境能引导学生探索作法？

学生的已有认知包括小学已知道线段是轴对称图形，六年级刚学习了线段的和差、线段的中点等;已有操作体验包括会用对折线段获得线段的中点，会作一条线段等于已知线段。但学生刚刚接触尺规作图，这方面的认知几乎是空白，需要从画图、操作等入手让学生不断积累经验，一步一步有序地过渡到用直尺和圆规作图。从学生已有认知与操作体验出发，设置合理问题，引发学生思考与探索，将成为教学的关键。

三、教学设计要点

先设计《先行研学单》发给学生。

1.依据所学内容，回顾并回答下列问题：（1）什么是线段的中点？（2）由点O是线段AB的中点，你可以得到哪些结论？

2.独立思考，并操作尝试回答下列问题：

（1）已知线段AB，找到一点O把线段AB分成相等的两条线段，你有哪些方法？

（2）已知线段AB，用直尺和圆规作线段EF，使EF=2AB，你有哪些想法？

（3）线段是轴对称图形吗？你是怎么想的？

（4）已知线段MN，用直尺和圆规作线段MN的中点O，并写出你的想法。

上课前，学生独立思考、操作尝试，写下自己的想法与操作。

教师依据学生的想法设计教学过程，组织教学。课堂上，教师选择能引发学生认知冲突的操作与想法，促使所有学生思考，以交流的方式，促进学生思维的发展与形成，真正理解作法。

四、思维发展脉络

1.思维起点—认知再现

问题1  已知线段AB，找到一点O把线段AB分成相等的两条线段，你有哪些方法？

学生的大脑不是一个空瓶子，教师设计的问题要能够唤醒学生的已有经验，引发他们进一步

思考。

这个问题，多数学生能想到用尺子量出AB的长，再除以2，以找到中点;或通过折叠，把点A和点B折到一起，折出中点。使用第一种方法是依据线段的中点的定义;使用第二种方法是依据线段是轴对称图形。这些都是学生的已有经验。

问题2  用直尺和圆规作线段EF，使EF=2AB，你有哪些想法？

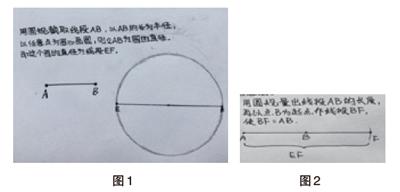
教师出示学生1的操作与想法。（见图1）

师：这位同学这样做，可以吗？

生：很好呀！直径等于半径的两倍。

教师出示学生2的操作与想法。（见图2）

师：这样可以吗？

生：我有个疑问，他怎么能保证那三个点在同一条直线上？

师：这个问题问得好！

教师出示学生3的操作与想法。（见图3）

师：这位同学的办法怎么样？

生：这个办法好，保证了三个点在一条直线上。

“倍”和“分”是互逆的。相对于“分”，“倍”更容易点，从《先行研学单》中可以看出学生们在寻找解决问题的方法。第一位同学运用了圆的直径是半径的2倍作出一条线段的2倍;第二位同学是想顺次截取，但不在一条射线上;第三位同学基本实现了作图要求。

学生们想到了使用圆规画出相同的半径，这一点非常可贵。出示他们的研学单，有利于启发学生聚焦用“相同的半径”作圆。这个问题的设置为后面启发学生进一步思考奠定了基础。

问题3  线段是轴对称图形吗？

生：我认为线段是轴对称图形，因为沿着一条直线对折，直线两旁的部分可以重合，这个特征符合轴对称图形的特征。

师：这个证据很充分，线段的确是轴对称图形。

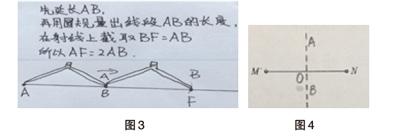
教师出示学生4的操作与想法。（见图4）

师：这位同学还画出了线段的对称轴。你猜，线段的中点在哪里？

生：就是對称轴和线段的交点呀！

通过课堂对话，学生明晰线段是轴对称图形，对称轴和这条线段的交点就是线段的中点。这为后面学生研究尺规作图奠定基础—如果可以通过尺规作图找到线段的对称轴，那么就能找到线段的中点了。

2.思维起步—模仿操作

问题4  用直尺和圆规作已知线段MN的中点O，请写出你的想法。

教师出示学生5的操作与想法。（见图5）

师：这位同学说，把线段割下对折来找中点，合理吗？

生（笑）：合理是合理，但总是把纸割下来好像不太妥当。

教师出示学生6的操作与想法。（见图6）

师：这位同学要把直尺折断找中点，可以吗？

生（笑）：这样不好吧。

可以看出学生的思维停留在“对折”这个层面，这就是学生们的认知起点。教师要通过课堂对话让学生明白这种作法的合理性以及局限性，把学生思维引向思考深处。

3.思维导入—尝试验证

教师出示学生7的操作与想法。（见图7）

师：有人想出了这样的办法，你赞同吗？

生：这个办法好是好，问题是圆心怎么找出来？

师：有同学想出了这样的办法——

教师出示学生8的操作与想法。（见图8）

师：如果他一直试，一直试，终究有一天能找到那个中点，是吗？

生（笑）：不能。

这两位同学在作圆的过程中已经意识到了MN的存在，他们试图在线段上找到一个点，让这个点到线段两个端点的距离相等。通过对话，学生意识到这个点很难一下子找到。

不过，有进步的是，学生意识到可以作圆。这是学生们一次有益的尝试，他们希望找到以MN为直径的圆的圆心，圆心就是此线段的中点。据说有个学生画了半小时还是没有找到圆心的位置。

4.思维发展—有序思考

教师出示学生9的操作与想法。（见图9）

师：有人想出了这样的办法，干脆从两头作圆，可以吗？

生：这想法很好。如果两个圆的半径正好相等，又正好有一个交点，那么那个点就是线段中点。

生：如果我能找到那样的圆的半径，中点不就找到了吗？

生：要恰好半径等于MN，太难了。

师：嗯，这两个圆的半径和哪条线段有关？

生：和线段MN的有关。

师：除了正好等于这条线段的外，还有哪些可能性？

生：小于它的，或者大于它的。

师：半径小于MN的的话，可以吗？

生：不行，那样交不住。

师：那么大于MN的呢？

生：那就有两个交点！

既然无法从线段内部找圆心，不妨从线段的两个端点开始作圆。显然，这位同学也是想作圆，而且是以线段的两个端点为圆心，以MN为半径作圆。这个想法好吗？当然很好，但是这样作图存在的问题是

MN这条线段也不好找。

5.思维形成—“发现”作法

问题5  分别以点M、N为圆心，适当长为半径作圆，说说你的作图。

生1：我作的两圆不相交。（见图10左）

生2：我作的两圆相交。（见图10右）

师：为什么有的同学画的两圆会相交，有的不相交？

生：当半径大于MN时，两圆相交。当半径小于MN时，两圆不相交。

师：那么，怎样找到线段MN的中点？

生：连结两个交点画一条线，那就是这条线段的对称轴！对称轴和MN的交点就是MN的中点。

师：真不错！（出示PPT，师生共同总结作图步骤，并作图）

这一环节的一个重大突破点在于学生从最初“在线段上找圆心”，变成“以线段的两个端点作为圆心”，这个转变直接促成了作图方法被发现。在学生不断否定自己最初的想法，逐渐走向清晰和明朗的过程中，教师的点拨极为重要。通过对话，让学生自己说出所作两圆的半径都和线段的一半有关。再通过分类，发现作法，这样“以大于线段的长为半径”就被大家发现了！

这个点找到了，但是它真的是线段的中点吗？有办法验证吗？由于在这个阶段，学生还没有学习全等三角形等知识，无法进行形式化的证明。教师可以引导学生思考别的检验方法，比如，可以用圆规检验这个点到线段两个端点的距离是否相等。

五、教后反思

1.为什么要协助学生自我建构

儿童认知心理学家皮亚杰认为，儿童的数理知识是无法通过告知获得的，只有在活动中“建构”。这种看似“低效”的讨论实际上是一种“互惠式”的谈话，学生在这个过程中积极思考，寻求更合理的解决方案，最终达成共识，实现自我建构。

笔者曾用“告知”的方式两分钟告诉学生作法，再做重复性练习。令人难堪的是，无论练习多少遍，无论考试考得多好，大部分学生一段时间后还是把作图的方法“还给老师”了。对比告知型的教学，这样的课看起来花费的时间多了，但有意思的是，在没有大量练习的情况下，过一段时间，所有人都能准确地作出线段中点。

2.学生的思维获得了怎样的发展

《义务教育阶段数学课程标准（2011年版）》指出，学生的数学学习内容应当是现实的、有意义的、富有挑战性的，这些内容要有利于学生主动进行观察、实验、猜测、推理、验证与交流。有效的数学活动不能单纯地依赖模仿和记忆，动手实践、自主探索和合作交流才是学生学习的主要方式。

从中可以看出，数学学习活动要有利于发展学生的数学素养，提升思维品质。在上这节课之前，教师需要问问自己：“大于线段的1/2长为半径作圆”这个作圖方法是怎么想出来的？学生能不能想出来？设计什么样的问题可以让学生自己想出作图的方法？

学生认知的起点是会作一条线段的2倍，知道线段是轴对称图形。教学的重要目标是让学生想出作图的方法。教师的作用是以学生课前的独立思考为基础，有逻辑地组织讨论，引导学生再次有序思考。从教学过程看，课前学生的思维水平处于混乱无序的状态，在交流的过程中逐渐走向有序和清晰，最终学生自己发现了作图的方法，实现了群体的自我建构，思维获得了发展。

3.有思考的交流才是生动的、有效的

课堂讨论的内容建立在学生课前的独立思考的基础上，交流过程中，学生们积极分享、展示自己的想法，不断否定自己最初的提案，又不断优化原有的想法。当这个作法被我们发现的时候，全班响起了热烈的掌声，学生们按捺不住激动的心情争着要上讲台尝试自己作图。

这样的课堂才是生动而有活力的，才有利于学生思维的发展。

（作者单位：上海赫德双语学校）

责任编辑：胡玉敏

huym@zgjszz.cn