尺规作图重在引导学生“想”数学

胡赵云

编者按

尺規作图是初等数学的古老话题，在教育人们思考数学、发展几何直观与推理能力等方面有着独特的意义。现实教学对尺规作图的功能研究不多，对它的教育价值缺乏足够的认识。本专题从尺规作图的价值与教学实践等角度阐述尺规作图教学要立足于引导学生思考，学会“想”数学。

一、概况介绍

尺规作图是指规定只能用直尺和圆规两种工具的作图，也称为初等几何作图或欧几里得作图。尺规作图分为定位作图与活位作图。定位作图是指所求作的图形必须在指定条件的位置，如“作已知角的平分线”。活位作图是指所求作的图形没有明确指定的位置，如“作一个角等于已知角”。

尺规作图必须遵守下列三条作图公法：

（1）过两点可以作一条直线;

（2）以定点为圆心及定长的线段为半径可以作圆;

（3）两条直线，或一条直线和一个圆，或两个圆，如果它们相交，就可以确定它们的交点。

《几何原本》的五条公设中第1.1、1.3条公设正是上述前两条公法。由此，欧几里得限制了作图工具只能是直尺和圆规，也规定了直尺和圆规只具有下列功能：

（1）作线：用直尺可以作出第一条公法所规定的直线;

（2）作圆：用圆规可以作出第二条公法所规定的圆;

（3）确定交点：用直尺和圆规可以确定出第三条公法所规定的交点。

从已知条件出发，经过有限次使用直尺和圆规作出所求作的图形，就说该作图问题有解。如果符合已知条件的图形不存在，就说该作图问题无解。作图不能与作图无解是不同概念。作图不能是由于受到作图公法和工具的限制而无法作出所求作的图形。例如，“三等分任意一个角”是尺规作图不能。

尺规作图题一般包括已知、求作、分析、作图、作法、证明、讨论七个方面内容。

分析，一般通过绘画草图，结合有关概念、公理、定理、基本作图，思考条件与所求作图形之间的联系，寻找作图的方法与步骤，积累“想”数学的经验。通过证明验证作出的图形与题设条件相符，发展学生的推理能力。几何作图既蕴含着几何证明，又能很好地培养发展几何直观。通过尺规作图作出几何图形实现对数学操作实验的抽象，形成并建立理念状态下的数学，建立不受物理形态影响的几何体系。

二、现状分析

1.数学课程标准的定位

《义务教育数学课程标准（2011年版）》（以下简称《课标》）中关于尺规作图的要求如下：

（1）能用尺规完成以下基本作图：作一条线段等于已知线段;作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线;过一点作已知直线的垂线。

（2）会利用基本作图作三角形：已知三边、两边及其夹角、两角及其夹边作三角形;已知底边及底边上的高线作等腰三角形;已知一直角边和斜边作直角三角形。

（3）会利用基本作图完成：过不在同一直线上的三点作圆;作三角形的外接圆、内切圆;作圆的内接正方形和正六边形。

（4）在尺规作图中，了解作图的道理，保留作图的痕迹，不要求写出作法。

与《全日制义务教育数学课程标准（实验稿）》相比，《课标》增加了“了解作图的道理”。这个“道理”是指尺规作图的作法与依据是什么，为什么这样作，以及想出作法的道理。

2.教科书的做法

我们选择人民教育出版社（以下简称“人教版”）、北京师范大学出版社（以下简称“北师大版”）、华东师范大学出版社（以下简称“华师大版”）、浙江教育出版社（以下简称“浙教版”）出版的数学教科书中关于尺规作图内容作比较。

（1）关于基本作图

为了简化表述，将五条基本作图用序号表示为：（a）作一条线段等于已知线段;（b）作一个角等于已知角;（c）作一个角的平分线;（d）作一条线段的垂直平分线;（e）过一点作已知直线的垂线。

表1 编排顺序比较

人教版 北师大版 华师大版 浙教版

（a）七上第4章 （a）七上第4章 （a）七上第4章 （a）七上第6章

（b）八上第12章 （b）七下第2章 （b）七上第4章 （c）八上第1章

（c）八上第12章 （d）七下第5章 （c）八上第13章 （b）八上第1章

（e）八上第13章 （c）七下第5章 （e）八上第13章 （d）八上第1章

（d）八上第13章 （e）八下第1章 （d）八上第13章 （e）八上第1章

①编排顺序比较（见表1）

从表1可知，基本作图（b）至（e）各版本教科书的编排顺序有所区别。除北师大版将基本作图（e）安排在八下第1章外，其他各版教科书都在八上讲完。

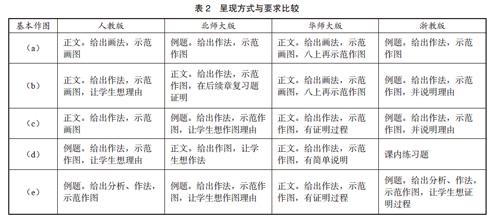
②呈现方式与要求比较（见表2）

各版本教科书关于五条基本作图的呈现方式均有所区别，有的安排在正文介绍，有的作为例题解答，有个别作为习题供学生练习。具体要求也有区别，表现在有分析与没有分析，完整呈现作法或者提出问题让学生想作法，作图后的结论有的给出证明，有的只给出简单的说明或者只问学生为什么正确。

表2 呈现方式与要求比较

基本作图 人教版 北师大版 华师大版 浙教版

（a） 正文。给出画法，示范画图 例题。给出作法，示范作图 正文。给出画法，示范画图，八上再示范作图 例题。给出作法，示范作图

（b） 正文。给出作法，示范画图，让学生想理由 正文。给出作法，示范作图，在后续章复习题证明 正文。给出画法，示范画图，八上再示范作图 例题。给出作法，示范作图，并说明理由

（c） 正文。给出作法，示范画图 例题。给出作法，示范作图，让学生想作图理由 正文。给出作法，示范作图，有证明过程 例题。给出作法，示范作图，并说明理由

（d） 例题。给出作法，示范作图，让学生想理由 正文。给出作图，让学生想作法 正文。给出作法，示范作图，有简单说明 课内练习题

（e） 例题。给出分析、作法，示范作图 例题。给出作法，示范作图，让学生想作图理由 正文。给出作法，示范作图，有证明过程 例题。给出分析、作法，示范作图，让学生想证明过程

从表2可以看出，各版本教科书大都以直接叙述作法、示范作图为主要呈现方式，对基本作图或基于基本作图的作图题的作法如何想出来缺少分析，帮助引导学生“想”数学的体验不足。

（2）其他作图内容

各版本教科书除了落实《课标》“会利用基本作图作三角形、圆、三角形的外接圆与内切圆、正四边形、正六边形”等内容外，还有一些不同的处理方式。例如，北师大版教科书编制了较多作三角形、等腰三角形有关的作图题;华师大版教科书编制了作平行四边形、矩形、菱形的内容;浙教版教科书编制了较多的作图问题，如与轴对称、中心对称、旋转图形，平行四边形、最短的弦、n等分线段、黄金分割点等有关的例题与习题。从中可看出，浙教版教科书对尺规作图的题型多于其他版本教科书的题型，要求也高于《课标》。

（3）作图与画图

长期以来，初中数学习惯用“作图”表示尺规作图，用“画图”表示可以借助刻度尺、三角板、量角器、丁字尺、缩放尺、比例规等工具作图。多数版本教科书仍沿用这一惯例。如北师大版教科书在轴对称、中心对称、旋转图形中就用“画图”表达，而人教版教科书对此不作严格的区分。

3.教学现状

当前，尺规作图问题一般只要求作出图形，保留痕迹，不写作法。随着尺规作图要求的降低，教学重视程度跟着下降，导致课堂教学中，涉及尺规作图的内容时，教师很少引导学生分析思考作法，更多地采用教师示范、学生模仿，或者学生一边听教师叙述作法一边作图的方式。这种讲授—记忆式的教学使得学生体验不到思考的乐趣，其效果也就可想而知了。例如， 2018年广东省中考卷有一道尺规作图题。

如图1，BD是菱形ABCD的对角线，∠CBD=75°。

（1）试用尺规作图法，作AB的垂直平分线EF，垂足为点E，交AD于点F。（不要求写作法，保留作图痕迹）

（2）略。

这是基本作图题“作已知线段的垂直平分线”的再现。教科书中有明确的讲解，相信教师也会教，但考试结果却令人意外。有一批学生交了白卷，错误的作法多种多样，如下。

这从侧面说明，失去思考，只以模仿、记忆方式的作图教学，学生终究还是不会。

三、教会学生“想”数学

1.从基本作图的作法想起

基本作图是尺规作图的基础，其作法相对简单。因处于尺规作图的起始阶段，如何想出作法就显得尤为重要。引导缺少经验的学生想到作法特别困难，以至于教科书、教师往往采用直接告知的简单方式。例如，作一个角等于已知角。教科书通常写成：

这个作法是怎么想到的？怎么会想到用圆规画弧？学生能经过自己独立探索而想出作法吗？如果不能，教师能给予哪些帮助？

如果这是七年级的学习内容，教师可以设计如下一组问题串：

（1）两个角相等什么意思？

（2）你有哪些方法理解两个角相等？

（3）你有哪些方式理解两个角重合？

（4）你会用什么方式说明两个角开口相同？

通过以上问题，引导学生思考如何将角的相等问题转化为线段或弧的相等问题，从而得到作弧的想法。如果这个问题在“三角形全等”后学习，就可以有更多的问题组设计方式。其他的基本作图问题，也可以采用类似的方式处理。

2.作图题重在怎样想出作法

尺規作图的乐趣在于想出作法。遇到作图题，学生无从下手时，教师不应直接告知作法，更不应该让学生看教师示范后再模仿重复作一次，而是应该设计恰当的问题，引导学生思考，帮助学生积累思考的经验，学习如何从已知的定理、熟悉的作图题、常见的图形与结论中想到作法。

例1 尺规作图：作∠A=36°。

学生可能尝试将平角五等分，但不易实现。

在学生思考未果后，教师可以设计问题串引导学生思考：

（1）能将这个角放在三角形中解决吗？

（2）你能想起一个熟悉的含有36°内角的三角形吗？是个什么样的三角形？画一画。

（3）这个三角形有什么特征？

（4）能用尺规作图找到线段AB的黄金分割点P吗？

（5）BC，PC，AB，AC之间有什么关系？

（6）你能用尺规作出，使AB=AC，BC=AB吗？

例2 已知△ABC，如图，在△ABC所在的平面内，作点P，使∠APB=2∠C。

在学生思考未果后，教师可以设计问题串引导学生思考：

（1）与“一个角是另一个角的2倍”有关的概念、定理、图形，你见过吗？请说一说，画一画。

（2）点A，B，P，C能成为角平分线图形上的点吗？

（3）等腰三角形顶点的外角是底角的2倍，能让你想到这个问题的作法吗？

（4）同弧所对的圆心角是圆周角的2倍，能让你想到这个问题的作法吗？

本问题可以进一步讨论：这样的点P有多少个点？这些点形成什么图形？

3.关联能引导学生想作法

想，可以是顿悟、灵感，可以是归纳、特殊化，也可以是类比、关联。尺规作图的关联表现在多方面。作图题不同，但作图依据有关联，如“作一个角的平分线”“作一条线段的中点”“作一条线段的垂直平分线”“过一点作已知直线的垂线”等的作图都是构造等腰三角形，都是依据等腰三角形性质证明的。作图题的表达方式各异，但作图的构想是相同的，如：

（1）已知线段AB，在线段AB上作点P，使AP2=AB·PB。

（2）已知线段a，b，作线段c，使线段c是线段a，b的比例中项。

（3）已知长方形ABCD，作正方形EFGH，使得它的面积等于长方形ABCD的面积。

（4）尺规作图：作∠A=36°。

（5）作已知圆的内接正五边形。

（6）已知线段a，作正五边形ABCDE，使AB=a。

这些作图题表达方式有别，但本质都是作两条线段的比例中项。经常引导学生关联已有积累，思考数学问题的解决，可以提高学生“想”数学的能力。

4.研究图形性质从作图开始

认识研究几何图形的性质，常常从操作开始，让学生“经历观察、实验、猜测、计算、推理、验证等活动过程”，探索几何图形的性质。诸多教科书设计了这些活动，如图8。

图8

课堂中，教师会据此设计如下问题：

（1）△ABC是等腰三角形吗？

（2）∠B与∠C有什么关系？

（3）∠BAD与∠CAD有什么关系？

（4）BD与CD有什么关系？

学生会得到，∠B=∠C，∠BAD=∠CAD，BD=CD，于是由此得出是等腰三角形的结论。但是，学生们会有疑问：∠B=∠C，∠BAD=∠CAD，BD=CD是因为纸片折叠重合得到的，是先有重叠再剪出等腰三角形，不是因为等腰三角形得出来的。怎样解决这个疑问？

可以用尺规作图解决。依次设计如下活动：

（1）尺规作图：已知线段a，b，作△ABC，使AB=AC=a，BC=b。

a                       b

（2）思考：△ABC是等腰三角形嗎？

等腰三角形一定有什么性质？你是怎么知道的？

两腰相等什么意思？能给我们什么启发？

（3）操作：剪下△ABC，将△ABC的两腰重合在一起。

（4）观察：△ABC的两腰重合时，你观察到什么？

两图形重合什么意思？从中你观察到什么？

尺规作图得到的等腰三角形是一般意义的等腰三角形，用它研究得到的性质具备一般性的结论，令人信服。其实，后续的平行四边形、矩形、菱形等图形性质的探索都可以采用这种方式。

可见，尺规作图是认识探索图形性质的有力工具。

（作者单位：上海赫德双语学校）

责任编辑：胡玉敏

huym@zgjszz.cn