灰色预测和0-1规划在供水问题中的应用
2020-08-08李泳澍
徐 畅 李泳澍
(1.重庆邮电大学 重庆南岸 400065;2.济南大学 山东济南 250022)
一、供水问题的提出
某村位于我国西南地区,平均年降水量不足20mm,是典型的缺水地区。过去村民的用水、依赖蓄水池和村中现有的四口水井。由于近年天气原因,蓄水池的功能完全丧失。而现有的四口水井经过多年使用后,年产水量逐渐减少。2009年以来,水井的产水量远远不能满足需要。为此,政府打算着手解决该问题。从两方面考虑,一是在该村附近又找到了8个可供打井的位置。二是通过铺设管道的办法从相隔20公里外的地方把河水引进该村。
可供打井位置共有8处,每处打井的费用和预计的年产水量不同。二是铺设管道,其费用为P=0.66Q0.51L(万元)。其中,Q表示每年的可供水量。从开工到完成需要三年时间,且要求完成之后,每年至少能提供100万吨的水。
要求从2010年开始,连续三年,每年最多可提供60万元用于该村的打井和铺设管道。为了保证该村从2010到2014年,每年分别能至少获得150、160、170、180、190万吨水,以此做出规划。
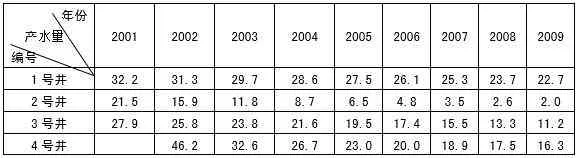
现有各水井在近几年的产水量(万吨)

8个位置打井费用(万元)和当年产水量(万吨)
二、模型的建立与求解
假设若只挖井不铺设管道,并且前三年的供水量恰好满足需水量。这样可使后面几年水的流失量减少,可近似实现最大供水的情况。通过计算发现,在这种情况下无法满足第五年的需水量。因此必须铺设管道。
(一)灰色预测模型
整体的供水量一部分来源于原水井的供水量。原水井的供水量大致呈下降趋势,我们通过建立灰色预测模型,得出未来5年原水井供水量的值,为后面问题的解决做出铺垫。下面以一号水井建立模型,通过原一号水井的产水量表,可建立出该井产水量时间序列如下:
q(0)=(q(0)(1),q(0)(2),q(0)(3),q(0)(4),q(0)(5),q(0)(6),q(0)(7),q(0)(8),q(0)(9))=(32.2,31.3,29.7,28.6,27.5,26.1,25.3,23.7,22.7)

同理预测出四口井在2010至2014的产水量如表1所示:

表1 2010年至2014原四口井的产水量
(二)打井和铺设管道计划
管道从开始铺设和到完工通水需要三年的时间,既需要打井满足需水量,又要最大可能地节约资金。在节约资金的前提下,在哪年打井,在什么位置打井成了问题的关键。已知在2010年时,原四口水井的产水量已经不能满足需水量,因此第一年必须打井。以打井的年份为标准,我们设计出了四种优化方案,即2010至2012年每年都打井、2010和2011年打井、2010和2012年打井、仅2010打井,为一二三四方案。之后进行方案求解,以一为例,其他同理可得。
若每年都打井,应先打产水量小的井,否则将会造成后面几年过多的水量的流失。要使三年的花费最小,则需要每年的花费都最小。设方案一花费的目标函数为:


利用MATLAB求解得x2=1,其余为0。第三年只打一个井,费用为6万。将这三年所用费用相加,即得到第一种方案的总花费:M11=19+5+6=31万。
同理求得四种方案所花总费用以及每年的出水量如表4所示:
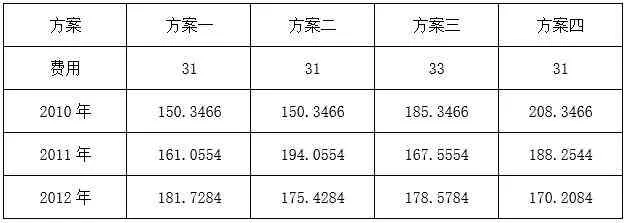
表4 四种方案所花总费用以及每年的出水量
四种方案具体的打井计划如表5所示:
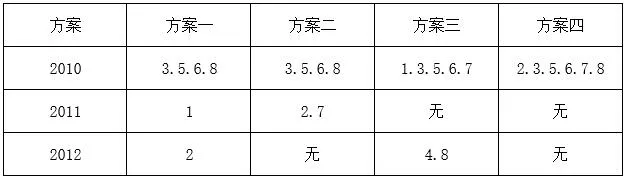
表5 四种方案具体的打井计划
利用铺设管道的方程 (万元),得到每种方案每年铺设管道的费用和长度如表6所示:
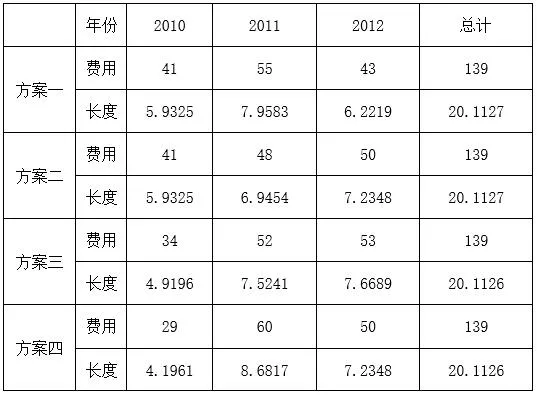
表6 每种方案每年铺设管道的费用和长度
进而我们得到:
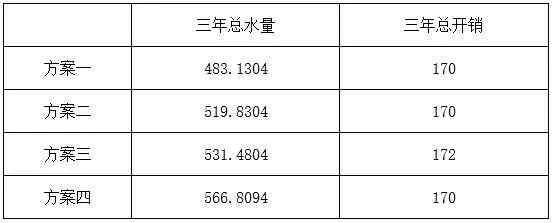
表7 四种方案的三年总水量及总开销
在节约资金的前提下,我们可得出花费最少且满足约束条件的方案为方案一、方案二、方案三。在花费最少的情况下,我们以三年总水量最多为最优方案,方案四。第一年打井3、5、6、8号,挖管道5.9325公里,花费60万;第二年打井1号,挖管道7.9583公里,花费60万;第三年打井2号,挖管道2.2219公里,完成目标,花费50万;总花费170万,节省10万。
