巧用题组练习 丰盈数学思考
2020-08-07肖群
肖群

摘 要:练习课是以学生独立练习为主要形式,是新授课的补充和延续,它可以使学生新学知识得到巩固,并逐步形成技能,对提高教学质量有十分重要的意义,在小学数学练习课上要注重题组设计,通过列举说理来加深对概念的理解;通过画图分析来寻求解题的思路;通过比较辨别来完善认知的结构;通过实践应用来增强解决问题的能力,从而提高练习课的效率。
关键词:题组;练习;思考
练习课是以学生独立练习为主要形式,是新授课的补充和延续,它可以使学生新学知识得到巩固,并逐步形成技能,对提高教学质量有十分重要的意义,因此在练习课中如何激发学生的练习兴趣,避免枯燥、单调地机械重复,提高练习课的效率,这便成了我们数学教师必须面对的问题。下面就谈谈自己粗浅的看法。
一、列举说理 加深对概念的理解
小学数学概念包括意义、性质、法则、公式、定理、定义等,这些基础知识是解决数学问题的主要依据,是发展智力、发展思维的理论基础。而对于一些容易混淆的概念,可以加强题组设计,通过列举说理,加深对概念的理解。
如:“数的整除”单元中的概念较多,且易混淆,在练习课上我就设计了一些判断题,以题组形式出现:
第一组①两个不同素数的公因数只有1。…( )
②公因数只有1的两个数一定是素数。…( )
第二组①自然数不是奇数就是偶数。…( )
②自然数不是素数就是合数。…( )
第一组第①题是对的,因为素数只有1和它本身两个因数,而两个不同素数的公因数只有1;而第②题可以采用列举法,如8和9的公因数只有1,但8和9都是合数,故此命题是错的。通过第一组的判断,能使学生更好地掌握“公因数只有1的两个数”可能的情况:①两个不同的素数;②1与任何自然数;③相邻两个自然数。如5和6、7和8……④连续的两个奇数;如7与9、13与15……⑤2与任何奇数;如2与5、2与9……
通过第二组的判断,能使学生更好地理解由于分类的标准不同,结果也不同,自然数按能否被2整除可分为奇数和偶数两大类,而按因数的个数来分则可分为质数、合数和1三类。而第二组中第②题这样说就正确了:除1以外,自然数不是素数就是合数;按因数的个数来分,自然数可以分为质数、合数和1。
再如:在教学分数的分类后,我设计了这样一组题进行判断:
①假分数的分子比分母大。………………( )
②分子比分母大的分数是假分数。…………( )
③分子比分母大的分数叫做假分数。………( )
①与②是两个互逆命题,①是错的,②是对的,学生做时也易混淆,通过此组题的练习,使学生对假分数的意义加深理解:假分数有两种情况,即分子比分母大的分数与分子和分母相等的分数。
举反例是判断的良策,每一个判断,每一步推理,力求让学生依据数学概念用数学语言说出理由,如果命题是错的还可要求学生将其改正,这样不但能加深对概念的理解,而且有助于培养学生的逻辑思维能力。
二、画图分析 寻求解题的思路
画图是解决问题的一种常用策略,通过画线段图,能搭起一座由已知条件通向未知条件的“小桥”,使所求问题迎刃而解。
例如:教学“列方程解应用题”以后,为了使学生能熟练地掌握用方程解与用算术方法,并能选择合适方法解题,我便设计了以下的一组题:
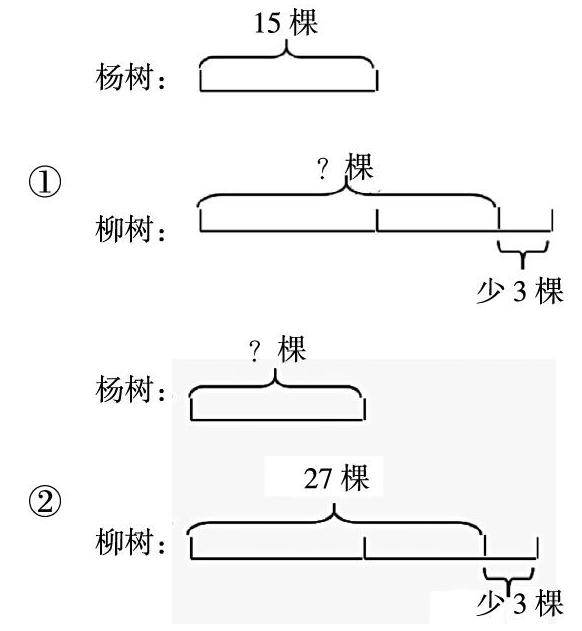
①杨树有15棵,柳树的棵数比杨树的2倍少3棵,柳树有几棵?
②柳树有27棵,柳树的棵数比杨树的2倍少3棵,杨树有几棵?
要求学生根据题目先画出线段图再列式解答:
通过画图分析可知,第①题中的一份,即杨树的棵数已知,适合用算式方法解,列式为:15×2-3=27(棵);而第②题中的一份未知,适合用方程来做。由于用方程解题过程较麻烦,也可用算术方法做:(27+3)÷2=15(棵),其中27+3求得杨树棵数的2倍是多少,再求杨树的棵数。
再如执教“最大公因数和最小公倍数的应用”时,学生解题方法经常出错,于是在练习时我设计了以下题组:
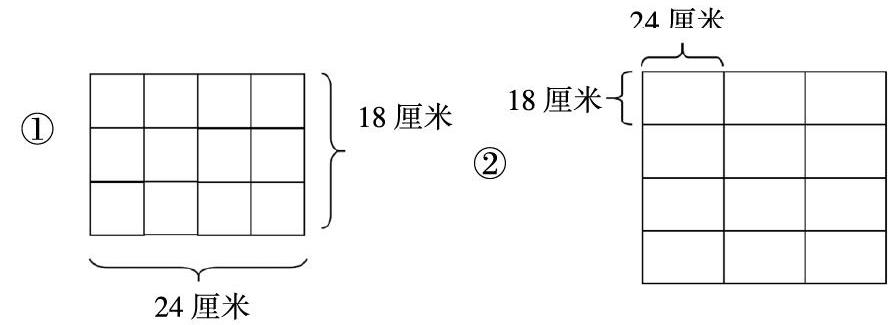
①一块木板长是24厘米,宽是18厘米,锯成相同的正方形木块,要求正方形木块的面积尽量大,而且木板没有剩余,锯成的正方形木块面积是多少?可以锯成多少块?
②一块木板长是24厘米,宽是18厘米,至少需要多少块这种木板能拼成一个较大的正方形木板,拼成的正方形木块面积是多少?
首先,要求学生根据题目先画出草图:
画的图进行分析:第①题中锯成的正方形木块的边长相当于长方形木板长与宽的最大公因数,而第②题中拼成的正方形木块的边长相当于长方形木板长与宽的最小公倍数。
再次,确定解答步骤,列式计算:
第①题 (24,18)=6 6×6=36(平方厘米)
(24÷6)×(18÷6)=12(块)
第②题 [24,18]=72 (72÷24)×(72÷18)=12(块)
最后,让学生比较这一组题,在解题思路上有何相同之处?从而得出,第一步无论是求最大公因数还是求最小公倍数,求出的都是锯成或拼成正方形的边长。
通过画图分析,不但增强了图文互补、图文并茂的效果,有利于学生找到题中的数量关系,理清解题思路,而且增强了学生分析、理解的能力。
三、比较辨别 完善认知的结构
在练习课中,要善于沟通新旧知识间的联系,加强题组设计,在比较、辨别异同中完善学生的认知结构,进一步加深学生对知识的理解。
如执教“认识分数”以后,我设计了以下题组:
這样设计练习,使学生在比较辨别中完善认知的结构,同时也有利于培养学生认真细致的审题习惯和思维的缜密性。
四、实践应用 增强解决问题的能力
新课标指出:“数学课程应遵循学生学习数学的心理规律,强调从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型,并进行解释与应用的过程。”学习数学的重要目的也在于用数学知识去解决日常生活、学习、工作中的实际问题。数学教学如果脱离实际,那数学学习就成了“无本之木,无源之水”,更谈不上学生有意义地学习数学和获得有意义的数学知识的目的。为此数学练习设计要考虑实践应用性,使学生在实践中运用知识、盘活知识,从而提高解决问题的能力。
例如,执教“圆的面积”后,在练习课上我设计了如下题组:
①在一个面积为16平方厘米的正方形内剪一个最大的圆,所剪圆的面积是多少平方厘米?
②在一个面积为12平方厘米的正方形内剪一个最大的圆,所剪圆的面积是多少平方厘米?
显然第①题很容易解答出来,根据正方形的面积为16平方厘米,可以求出正方形的边长为4厘米,圆的面积则为3.14×(4÷2)=12.56(平方厘米);而第②题如果按常规的思考方法:要求圆的面积,需先求出圆的半径,根据题意,圆的半径就是正方形边长的一半,但根据题中所给条件,用小学的数学知识无法求出,于是必须换个角度来考虑:可以设所剪圆的半径为r,那么正方形的边长为2r,由此可推出圆的半径平方等于3,就可以求出圆的面积了。随即又出现以下两题,要求分别求出圆的面积:
这样的练习设计,可以给学生以更广阔的学习数学的空间,学生学到的将不仅仅是数学知识本身,更重要的是观察、分析、交流、创新、实践等综合素质得到了培养和训练。
总而言之,在小学数学练习课上精心设计题组,通过列举说理来加深对概念的理解;通过画图分析来寻求解题的思路;通过比较辨别来完善认知的结构;通过实践应用来增强解决问题的能力,从而丰盈数学思考,提高练习课的效率。
编辑 王亚青
