短波令牌环传输顺序优化

李程文 李迟生 林梦思 吴小晴

摘  要： 短波令牌环分布式自组织和无竞争机制有效避免了短波数据通信访问冲突问题，为短波通信提供良好的多址接入方式。针对短波令牌环中可能存在不必要中继节点产生的令牌开销影响网络吞吐量和时延等问题，转化为求解整个短波令牌环最优传输顺序表，提出Floyd和遗传算法联合算法对短波令牌环传输顺序进行优化。结果显示优化后的传输顺序表减少了不必要的中继次数，验证了算法优化短波令牌环传输顺序的有效性，并与单独使用Floyd算法或遗传算法进行对比，显示联合算法优化效果更好。通过分析表明，使用联合算法对短波令牌环传输顺序进行优化提升了网络吞吐量，减小了网络数据传输时延。

关键词： 短波令牌环; 短波通信; 中继减少; 传输顺序优化; 联合算法; 时延降低

中图分类号： TN915?34                        文献标识码： A                           文章编号： 1004?373X（2020）13?0011?05

Optimization of transmission order of shortwave token ring

LI Chengwen， LI Chisheng， LIN Mengsi， WU Xiaoqing

（School of Information Engineering， Nanchang University， Nanchang 330031， China）

Abstract： The shortwave token ring distributed self?organizing and non?competitive mechanism effectively avoids the shortwave data communication access conflict and provides a good multiple access mode for shortwave communication. For the problem that the possible token overhead generated by unnecessary relay nodes in the shortwave token ring may affect network throughput and delay， it is transformed into the optimal shortwave token ring optimal transmission sequence table， so a joint algorithm combining Floyd algorithm and genetic algorithm is proposed to optimize the shortwave order of the shortwave token ring. The results show that the optimized transmission sequence table reduces the number of unnecessary relays and verifies the effectiveness of the algorithm in optimizing the transmission order of the shortwave token ring. The result got by the joint algorithm is compared with those got by both Floyd algorithm and genetic algorithm. The comparative result indicates that the joint algorithm has better effect. The analysis conclusion shows that the shortwave token ring transmission order optimized by the joint algorithm can improve the network throughout and reduce the time delay of network data transmission.

Keywords： shortwave token ring; shortwave communication; relay cutting down; transmission order optimization; joint algorithm; delay reduction

0  引  言

短波令牌环协议[1]是實现多节点在同一广播信道中进行数据交互的MAC层协议，根据令牌数据对各个节点进行发送权利的控制，使得每个节点发送数据的机会公平且无冲突，避免了信道上的碰撞。同时，短波令牌环是一个自组织网络，拥有良好的自我修复能力，能有效解决单故障节点问题。将短波令牌环应用于短波通信中，有利于避免数据冲突，提供了较好的网络吞吐量和接入时延，强化了短波抗毁能力。

在节点数量多的情况下，短波令牌环由于网络拓扑变化可能产生不必要的中继，从而影响到整个网络的性能。针对中继引起的时延问题，考虑传输顺序的优化，即对整个环路长度的优化。在求得整个环路长度之前，需要求解每个节点对之间的最短距离。短波令牌环内节点可以监听其他节点是否能与自身直接通信，根据监听到的监听表，依次通过令牌传递给后继节点，后继节点更新传递的监听表，最终容易得到一个全部节点的监听表，再根据求解点与点之间的最短路径算法，可以得到求解封闭环路最短路径问题的输入参数。求解两点之间最短路径算法有Dijkstra算法[2]和Floyd算法[3]。

求解封闭环路的最短路径问题可以参考旅行商问题（TSP）的解法。TSP[4]是完全NP问题，目前对于TSP问题的解法有多种，包括动态规划法、分支定界法、遗传算法等。动态规划法[5]运用递归的思想，相比于全排列的情况降低了时间复杂度，但仍旧对于节点数目过大的问题没有快速地找出最优解。分支定界法[6]根据一个智能化的判定函数，只产生部分状态空间树，从而加速了搜索过程，但是该算法最坏情况的时间复杂度与动态规划法的时间复杂度一致，很少应用在大规模的问题中。遗传算法[7]是模仿生物学的自然选择和自然遗传，模仿生命进化来求解问题的最优解。遗传算法具有算法简单、易于实现、能够并行化和全局搜索能力等特点，且较传统的精确算法速度较快。

为了改善短波令牌环网络吞吐量和时延问题，考虑优化短波令牌环中的传输顺序表，将节点之间的距离用跳数表示。本文使用Floyd算法求解最小距离矩阵作为遗传算法的初始解，再使用遗传算法对短波令牌环周期长度进行求解，从而求得优化的传输顺序表。预期优化之后的传输顺序表比未优化的传输顺序表存在更少的中继节点个数，使环运行一周的时间减少，减少中继带来的时延，提高网络性能。

1  传输顺序优化问题

短波令牌环协议具有分布式自组织和无竞争等特点，适用于短波数据通信。节点与节点之间进行数据传输需要进行组网过程，首先当节点定时器到期后，节点将发出邀请组网信号，其他节点收到信号将等待一段时间后回应，节点收到回应则更新传输顺序表放入发送令牌中发送给下一节点，下一节点收到令牌更新传输顺序表并按照该表进行传输。

在短波令牌环协议中，令牌数据内的传输顺序表字段规定了每个节点发送数据的顺序，只有发送权轮到目标节点，目标节点才能发送数据。短波令牌环相比无线令牌环，增加了中继和环合并机制[8]。在没有中继机制的无线令牌环中，整个环路只与相邻节点进行数据传输，若节点与另一节点之间通信发生故障，自恢复机制丢弃不可到达节点，将通信范围内的其他节点作为新的后继节点，从而使整个环路封闭，此时整个环路的传输顺序已经是最优情况。考虑中继机制[9]的短波令牌环不是直接将不可到达的节点舍弃，而是通过判断不可到达的节点是否可以通过中继某个节点，使得整个网络形成封闭的环路。然而中继节点的数目是不确定的，从源节点到最终的目标节点之间可能存在多个中继节点。如果不对中继情况下的短波令牌环进行优化处理，整个网络环路将存在很多无意义的中继，导致环路的吞吐量下降，网络性能整体下降，如图1所示。

图1显示4节点情况下短波令牌环出现不必要中继的情况，其中节点C和节点D可以通信。所以优化传输顺序表可以使得整个网络的开销减少，尤其是网络节点之间需要中继多次所产生的时间成本，当网络节点的数据负载量过大时，将大大增加数据传输的时延。

2  问题分析

短波令牌环[10]网络可以用图[G（N，L）]来表示，其中[N]为环内节点数，[L]为节点对之间的链路。将短波令牌环中节点与节点之间通信所需跳数作为节点之间的距离，其传输顺序的优化可以转化为网络节点之间形成封闭环路的最短路径问题，即求环周期长度RCL的最小值：

同时，根据距离矩阵可以推出邻接矩阵：

计算RCL的最小值需要距离矩阵，距离矩阵的计算需要通过全局的邻接矩阵。单个节点产生的监听表只是局部邻接矩阵，所以需要至少经过一轮令牌传递将局部的距离矩阵转换为邻接矩阵，再与自身的局部邻接矩阵对比更新，最后得到全局邻接矩阵，短波令牌环传输顺序优化问题便可以进行求解。

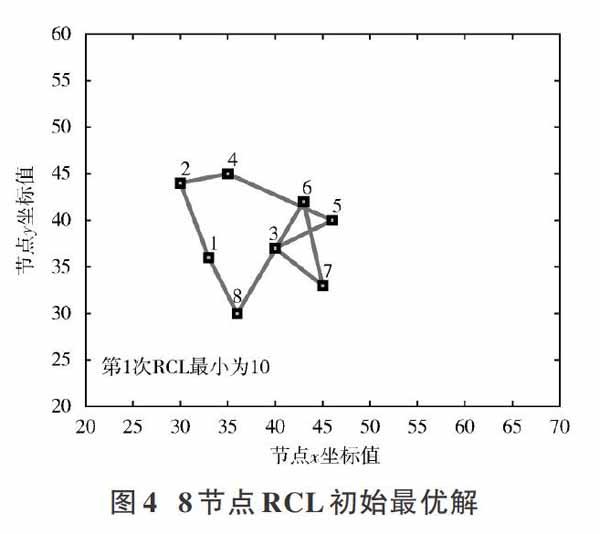
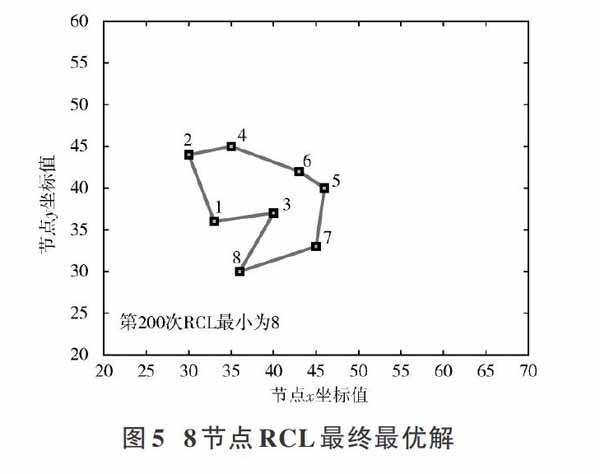
根据以上分析，短波令牌环传输顺序优化问题的求解过程如图2所示。

3  传输顺序联合优化算法

根据短波令牌环协议的要求，每个节点都存在一张监听表，记录节点与其他节点是否相邻，即能否直接通信。在组网开始时，节点与节点之间还未形成环路，所以需要通过令牌将邻接信息传递，此时节点传递的是局部距离矩阵，一个节点到另一个节点的距离将以四位二进制的形式依次放入令牌中，一个环内节点到节点的最长距离为15，即每个节点对之间最多能中继15次[11]。传输顺序表所占令牌字节数为：

式中Ceil（[x]）是大于或等于[x]的最小整数。

节点接收到前驱节点的局部距离矩阵，将根据式（2）得到局部邻接矩阵，当环路能稳定运行一个周期后，节点将收到所有节点的邻接信息。通过每一次的对比更新，形成全局邻接矩阵。以A，B，C，D四节点为例，如图3所示。

当A节点和B节点组网时，B节点将收到A节点传来的局部距离矩阵，此时B节点将其转化为局部邻接矩阵，并将B节点监听到的邻接信息插入到局部邻接矩阵，形成新的局部距离矩阵，并将其传递给C节点，C节点重复同样的工作，直到D节点将更新完的全局邻接信息传递给A，此时四节点环网已经组建完成。

得到全局邻接矩阵之后，开始考虑计算全局最小距离矩阵[DM]。根据Floyd算法得到节点对之间的最短距离之后，可以利用遗传算法求解RCL的最小值，结合每对节点之间的路径表得到最终优化后的传输顺序表。

本文联合优化算法步骤如下：

步骤1：节点接收到令牌数据，将得到的距离字段按式（2）进行转换，得到全局邻接矩阵[A]。

步骤2：初始化DM最小距离矩阵，将邻接矩阵[A]复制给[DM]矩阵。初始化传输顺序记录表TL，用于记录每对节点之间的顺序路径。

步骤3：根据下式找出每对节点之间的最小距离，更新DM矩阵和TL顺序表。

步骤4：传输顺序编码，为每一个节点标注序号，传输顺序用序列表示，随机产生[k]个不同顺序的序列。

步骤5：计算并评价每条序列的适应值[fi]。每条序列的适应值决定被选取的概率，适应值越大，被选取的概率越大。求解问题为RCL的最小值，适应值函数应选为RCL的倒数，根据所得全部序列的适应值，对所有序列進行评价，如下式：

参考文献

[1] NC3A. STANAG 5066： profile for HF data communications annex L， high?frequency wireless – token – ring – protocol requirements [S/OL]. [2012?06?17]. https：//ishare.iask.sina.com.cn/f/24968358.html.

[2] ZULFIQAR L， ISNANTO R， NURHAYATI O. Optimal distribution route planning based on collaboration of Dijkstra and sweep algorithm [C]// 2018 10th International Conference on Information Technology and Electrical Engineering （ICITEE）. Kuta， Bali Island： IEEE， 2018： 24?26.

[3] 潘立彦，张大成.改进Floyd算法在城市交通网络优化中的应用[J].物流技术，2018，37（11）：71?74.

[4] 刘云飞.基于TSP问题的仿生算法比较[J].电子技术与软件工程，2019（2）：110?111.

[5] 来学伟.动态规划法在TSP问题中的应用[J].吉林化工学院学报，2017，34（3）：65?67.

[6] 白云娇.关于分支定界法求解过程的补充和改进[J].科学咨询（科技管理），2017（27）：72?73.

[7] 馬骏.遗传算法TSP的Matlab求解分析[J].科技视界，2018（16）：37?38.

[8] 贺骁，李曼，白翔，等.短波令牌环协议的研究现状与发展[J].通信技术，2014（10）：1167?1172.

[9] JOHNSON E E， TANG Z， BALAKRISHNAN M. Token relay with optimistic joining [C]// 2005 IEEE Military Communications Conference. Atlantic City， NJ， USA： IEEE， 2005： 2216?2222.

[10] 贺骁，刘芸江，白翔，等.短波地空IP网络的MAC协议设计与仿真[J].计算机应用与软件，2016，33（3）：138?142.

[11] 李灿.短波通信网令牌环协议应用研究[D].北京：中国舰船研究院，2014.