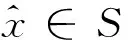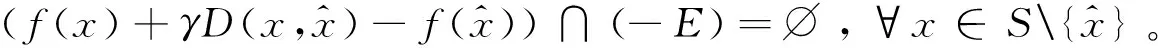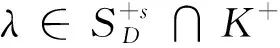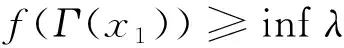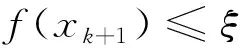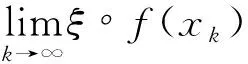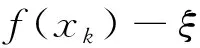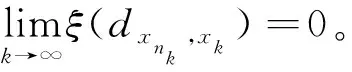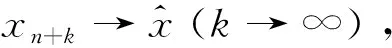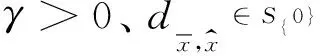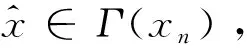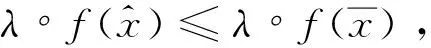向量优化问题中基于集值拟度量的广义Ekeland变分原理

万 轩

(重庆建筑科技职业学院 基础教学部，重庆 401331)

0 引言

1972年，Ekeland[1-2]给出了一个变分原理，现在称为Ekeland变分原理，它指出对于在完备度量空间中关于带扰动的下半连续函数取严格极小值。在过去的40多年中，著名的Ekeland变分原理已广泛应用于不动点理论、博弈论、数学规划、控制理论等，因此，Ekeland变分原理是非线性分析和优化中最受欢迎的理论工具之一。受到这种广泛用途的启发，许多作者一直对在向量空间中获得Ekeland变分原理有着非常浓厚的兴趣，见文献[3-10]等。

特别地, Bednarczuk[5]在局部凸空间中提出了给定以有界凸子集乘以距离函数为扰动的单调半连续映射的向量值Ekeand变分原理，并根据这类向量值Ekeand变分原理研究了近似解的一些性质。Gutiérrez等[6]引入了集值度量，并通过使用它，将著名的数值Ekeland变分原理扩展到向量值映射，获得的新的Ekeland变分原理比之前的Ekeland 变分原理更为广泛，主要是考虑了集值扰动映射和不再依赖于任何ε-有效解的概念。同时还推出了几种涉及向量优化问题的近似解的特殊形式的Ekeland变分原理，并讨论了它们的应用。然而，在这里，需要假设锥是ω-正则的，这个要求限制了新Ekeland变分原理的适用范围。Qiu[7]考虑了一种比文献[6]更一般的概念：集值拟度量，并引入了集值拟度量与原始度量之间的兼容性概念，通过这个概念给出了一个广义集值Ekeland变分原理，其中扰动项包含了与原始度量兼容的集值拟度量。这里不再需要假设锥是ω-正则的，并且从这个广义的集值Ekeland变分原理中，推出了一些适用于向量优化问题中的近似解的特殊形式的集值Ekeland变分原理，从而改进和推广了文献[6]中的相关结果。万轩[8-9]利用完备拟度量空间中具有Q-函数的数值Ekeland变分原理和局部凸空间中向量值Ekeland变分原理给出了广义向量值Ekeland变分原理并研究其等价性。万轩等[10]利用非线性标量化函数和Q-函数等工具对Ekeland变分原理进行了进一步的推广，在拟度量空间中建立了具有Q-函数的集值Ekeland变分原理。

另一方面，改进集也受到了广泛关注，其在向量优化问题研究发挥着十分重要的作用，见文献 [11-16]等。Chicco等[11]在有限维空间中基于comprehensive集提出了改进集的概念，并研究了其一些拓扑性质。随后，Gutiérrez等[12]将改进集及E-有效解概念推广到了一般拓扑线性空间，并研究相关性质。Zhao等[13-14]在改进集的基础上提出了邻近E-次似凸性概念、向量优化问题弱E-最优解和E-Benson真有效性的概念，并建立了相应的择一性定理等。万轩等[15-16]利用非线性标量化函数以及相应的非凸分离定理在局部凸空间中建立了具有改进集的集值Ekeland变分原理，并给出相应的具有改进集的集值Caristi-Kirk不动点定理、集值Takahashi非凸极小化定理和集值Oettli-Théra定理，以及研究它们的等价性。

受文献[6,7,10,13-15]研究工作的启发，本文借助于集值拟度量、正极锥和改进集等工具，在完备度量空间中研究广义的集值Ekeland变分原理，其中扰动项包含一个与原始度量相兼容的集值拟度量。本文所建立的新的集值Ekeland变分原理以一些经典形式的Ekeland变分原理作为其特例。

1 预备知识

在本文中, 设(X,d)为非平凡完备度量空间，Y为局部凸空间，Y*表示Y的拓扑对偶空间，R表示实数集，N为自然数集，N+为正整数集。对任意ξ∈Y*，在Y中定义连续半范数pξ：

pξ:=|ξ(y)|，∀y∈Y。

设A,B∈Y，α∈R，则定义集合A+B和αA为

A+B:={z∈Y:z=x+y,x∈A,y∈B}，

αA:={z∈Y:z=αx,x∈A}。

对任意非空集合A⊂Y，记int(A)，cl(A)，conv(A)和cone(A)分别表示集合A的内部，闭包，凸包和锥包。非空集合K⊂Y满足对任意α≥0有αK⊂K，则称K为锥；若锥K满足K+K⊂K，则称锥K为凸锥；若锥K满足K∩(-K)={0}，则称锥K为点锥；若锥K满足K≠{0}，则称锥K为非平凡的。

假设int(K)≠∅，在Y中定义关于凸锥K的偏序“≤K”为：

x≤Ky⟺y-x∈K，∀x,y∈Y。

考虑如下向量优化问题：

(P) min {f(x):x∈S}

其中向量值函数f:X→Y，非空集合S⊂X为闭集。称点x0∈S为问题(P)的有效解，若

(f(S)-f(x0))∩(-K

其中f(S)=∪x∈S{f(x)}。

正极锥K+和严格正极锥K+s分别定义为：

K+={ξ∈Y*:ξ(k)≥0,∀k∈K}，

K+s={ξ∈Y*:ξ(k)>0,∀k∈K

定义2[7]若集值映射D:X×X→2K满足：

(i)D(x,y)≠∅，D(x,x)={0}，∀x,y∈X和0∉D(x,y)，∀x≠y；

(ii)D(x,y)=D(y,x)，∀x,y∈X；

(iii)D(x,y)+D(y,z)⊂D(x,z)+K，∀x,y,z∈X，

则称集值映射D为集值K-度量，若条件(ii)不成立，则称集值映射D为集值K-拟度量。

在下文中，我们总是假设集值映射D为集值K-拟度量，除非另有说明。设

SD:=cone(conv(∪{D(x,y):x,y∈X}))，

ED:=(SD

定义3[6-7]设K⊂Y为凸锥，M⊂Y为非空集合。若对任意ξ∈K+使得

inf{ξ(y):y∈M}>-∞，

则称M为K-有界。

Γ(x):={z∈S:(f(z)+γD(z,x)-f(x))∩(-E)≠∅}。

显然，有x∈Γ(x)，故通过集合Γ(x)可得一个集值映射Γ(·):S→2S

定义5[7]若δ>0，记集合

Dδ:=∪d(x,y)≥δD(x,y)。

若对任意δ>0，任意序列{zn}⊂Dδ，存在ξ′∈K+使得ξ′(zn)→/0(n→∞)，则称集值K-拟度量D是关于原始度量d相容。

2 主要结果

本节主要利用改进集和集值K-拟度量建立一种新的广义集值Ekeland变分原理，并讨论它一些特殊形式。

证明设任意z∈Γ(x)和任意y∈Γ(z)，

(f(z)+γD(z,x)-f(x))∩(-E)≠∅，

(f(y)+γD(y,z)-f(z))∩(-E)≠∅。

则存在d1∈D(z,x)，d2∈D(y,z)和存在e1,e2∈E使得

f(z)+γd1-f(x)=-e1，f(y)+γd2-f(z)=-e2。

相加可得

f(y)+γ(d1+d2)-f(x)=-(e1+e2)。

(1)

通过集值K-拟度量的定义有

d1+d2∈D(z,x)+D(y,z)⊂D(y,x)+K，

存在d∈D(y,x)使得d1+d2∈d+K，因此

-(e1+e2)=f(y)+γ(d1+d2)-f(x)∈f(y)+γd-f(x)+γK，

f(y)+γd-f(x)∈-(e1+e2)-γK⊂-(E+E+K)=-E。

故(f(y)+γD(y,x)-f(x))∩(-E)≠∅，即y∈Γ(x)，通过y∈Γ(z)的任意性得Γ(z)⊂Γ(x)。

(i) 对任意x∈Γ(x0)有f(Γ(x))-f(x0)⊂(f(S)-f(x0))∩(-ED)；

(ii) 若集合(f(S)-f(x0))∩(-ED)是K-有界的，则对任意ξ∈K+使得ξ°f(Γ(x0))为下有界，即

inf{〈ξ,f(z)〉:z∈Γ(x0)}>-∞，

进一步，对任意x∈Γ(x0)使得ξ°f(·)在Γ(x)是下有界的。

证明(i)因为x0∈S，x∈Γ(x0)，由引理2.1可得Γ(x)⊂Γ(x0)⊂S，故

f(Γ(x))-f(x0)⊂f(S)-f(x0)。

(2)

因为x∈Γ(x0)，即

(f(x)+γD(x,x0)-f(x0))∩(-E)≠∅，

故存在d∈D(x,x0)使得f(x)+γd-f(x0)∈-E，即

f(x)-f(x0)∈-γd-E。

(3)

若x=x0，则f(x)-f(x0)=0，则利用集合ED的定义，有f(x)-f(x0)∈-ED；

若x≠x0，因为集值K-拟度量D的定义蕴含0∉D(x,x0)，所以d≠0。而γ>0，由集合SD的定义有γd∈SD

f(x)-f(x0)∈-γd-E⊂-(SD

利用x∈Γ(x0)的任意性和引理1可得

f(Γ(x))-f(x0)⊂f(Γ(x0))-f(x0)⊂-ED。

(4)

结合(2)式和(4)式可得

f(Γ(x))-f(x0)⊂(f(S)-f(x0))∩(-ED)。

(ii) 利用(4)式和Γ(x0)⊂S，则对任意ξ∈K+有

inf{〈ξ,f(z)〉:z∈Γ(x0)}

=inf{〈ξ,f(x0)+f(z)-f(x0)〉:z∈Γ(x0)}

=〈ξ,f(x0)〉+inf{〈ξ,f(z)-f(x0)〉:z∈Γ(x0)}

=〈ξ,f(x0)〉+inf{〈ξ,y〉:y∈(f(Γ(x0))-f(x0))∩(-ED)}

≥〈ξ,f(x0)〉+inf{〈ξ,y〉:y∈(f(S)-f(x0))∩(-ED)}。

(5)

因为(f(S)-f(x0))∩(-ED)是K-有界的，所以对任意ξ∈K+使得

inf{〈ξ,y〉:y∈(f(S)-f(x0))∩(-ED)}>-∞。

(6)

故由(5)式和(6)式可得

inf{〈ξ,f(z)〉:z∈Γ(x0)}>-∞，

(7)

即对任意ξ∈K+使得ξ°f(Γ(x0))是下有界的。

另一方面，对任意x∈Γ(x0)，利用引理1有Γ(x)⊂Γ(x0)，再结合(7)式可得

inf{〈ξ,f(z)〉:z∈Γ(x)}≥inf{〈ξ,f(z)〉:z∈Γ(x0)}>-∞。

从而可得对任意x∈Γ(x0)使得ξ°f(·)在Γ(x)是下有界的。

(Q2) 集值K-拟度量D是关于原始度量d相容；

(Q3) 对任意x∈Γ(x0)使得Γ(x)为动态闭集；

(8)

(9)

证明由(Q4)和引理2可知，对任意ξ∈K+有

inf{〈ξ,f(z)〉:z∈Γ(x0)}>-∞，∀ξ∈K+。

(10)

下面构造非常数序列{xn}⊂Γ(x0)。选取x1∈Γ(x0)使得

由x1∈Γ(x0)和引理1有Γ(x1)⊂Γ(x0)，

选取x2∈Γ(x1)使得

不失一般性，假设xn-1已经给定，选取xn∈Γ(xn-1)使得

(11)

无限地重复这个过程，可得序列{xn}⊂Γ(x0)使得xn∈Γ(xn-1)，故

Γ(xn)⊂Γ(xn-1)⊂···⊂Γ(x1)⊂Γ(x0)。

再结合(10)式可得对任意ξ∈K+有

≥···≥infξ°f(Γ(x1))

≥infξ°f(Γ(x0))>-∞，

(12)

下证{xn}⊂Γ(x0)是Cauthy序列。反证，假设{xn}⊂Γ(x0)不是Cauthy序列，则存在δ>0使得对任意k∈N+，存在nk>k有

d(xnk,xk)≥δ。

(13)

因xnk∈Γ(xnk-1)⊂Γ(xk)，则(f(xnk)+γD(xnk,xk)-f(xk))∩(-E)≠∅。故存在dxnk,xk∈D(xnk,xk)使得

f(xnk)+γdxnk,xk-f(xk)∈-E⊂-K。

(14)

因为dxnk,xk∈D(xnk,xk)，再由(13)式有

d(xnk,xk)≥δ>0，

故由(Q2)可知存在ξ'∈K+使得

ξ′(dxnk,xk)→/0 (k→∞)。

(15)

Γ(xn+k+1)⊂Γ(xn+k)⊂Γ(xn)。

从而(8)式成立。

(16)

(17)

由(16)式和(17)式可得

(18)

(19)

(20)

由(11)式、(19)式和(20)式可得

注1 若E=K

注2 若对任意x,y∈X有D(x,y)=d(x,y)K，则定理1可退化为文献[15]中定理3.1中λ=1的情况。