密闭空间爆炸温度动态不确定度评估方法研究

张 龙, 张继军, 赵建伟, 张宝国, 张东亮

(西北核技术研究院,陕西 西安 710024)

1 引 言

在密闭空间爆炸实验中,准确测量爆后气体的温度变化历程对于分析爆炸实施效果和气体扩散规律具有十分重要的意义[1,2]。由于爆炸过程具有极强的瞬时性和动态性,因此对爆后气体温度参数的测量属于动态测量范畴。与静态测量相比,动态测量具有波动性、随机性等特征,且动态测量过程容易受到多种未知随机误差的干扰[3]。为获得更加准确的爆后气体温度参数,希望在现有传感器的基础上通过数学方法减小被测量动态测量结果的随机性误差,并对其估计真值和动态测量不确定度做出准确评定。

在动态测量数据处理方法中,非统计理论表现出较强的优势[4],灰色系统理论[5]、Bootstrap方法[6]等算法在动态测量数据的不确定度评定中得到了广泛应用。在测量数据序列概率分布未知的条件下,灰色模型GM(1,1)可以准确预测被测量瞬时值的大小,但难以估计其置信区间,因而无法评估在给定置信概率下的动态测量不确定度[7,8];Bootstrap方法可以通过自助再抽样操作模拟动态测量数据序列的概率分布,并估计其置信区间,但计算机仿真结果表明,自助再抽样方法引入了附加的不确定度分量[9],并且由Bootstrap方法获得的估计区间小于原始数据的实际分布区间,从而增大了动态不确定度的估计误差。

综上所述,Bootstrap方法和灰色模型GM(1,1)均无法对密闭空间爆炸温度的动态不确定度做出准确评价。本文融合灰色模型GM(1,1)、Bootstrap方法以及不确定度评定理论,将灰自助模型GBM(1,1)运用到密闭空间爆炸温度动态测量不确定度的评定中,并选取估计真值、估计区间、区间估计可靠度、动态测量不确定度和平均不确定度等参数表征其估计结果。实验结果表明,GBM(1,1)模型融合了灰色模型GM(1,1)和Bootstrap方法的优势,能够准确模拟动态测量数据序列的概率分布,并实时跟踪被测量瞬时值的变化趋势。相比于灰色模型GM(1,1)和Bootstrap方法,灰自助模型GBM(1,1)具有更高的真值估计精度和区间估计可靠度,其区间估计可靠度高于90%,估计区间能够更加完整地包络被测量的动态波动范围。在密闭空间爆炸实验中,该方法能够对爆室温度的动态测量不确定度做出准确评估,具有较高的实用价值。

2 方 法

2.1 GBM(1,1)数学模型

设密闭爆室内气体的温度参数为随机变量,通过数据采集系统可获得被测量的动态测量数据序列为:

X={x(t)}, (t=1,2,…)

(1)

式中:x(t)表示t时刻的测量数据。从X中抽取t时刻之前的m个数据(包括t时刻的数据),构成时刻t的动态评估子序列Xm:

Xm={xm(n)},
(n=t-m+1,t-m+2,…,t)

(2)

根据Bootstrap方法,从Xm中有放回地等概率抽取1个数据,共抽取m次,得到第一个Bootstrap样本。重复上述方法B次,得到B个Bootstrap再抽样样本,用向量表示为:

YBoot=(Y1,Y2,…,Yb,),
(b=1,2,…,B)

(3)

式中Yb为第b个Bootstrap再抽样样本,且有

Yb={yb(n)},
(n=t-m+1,t-m+2,…,t)

(4)

式中:yb(n)为Yb中第n个Bootstrap再抽样数据。

在灰色系统理论中,累加生成是重要的数据处理方法。任意非负波动数列经累加生成操作后均可转化为递增数列,从而削弱了原始数据序列的随机性,突出其变化趋势,有助于发现数据内在的变化规律[10]。根据灰色模型GM(1,1),对Yb做一阶累加生成运算,其生成序列表示为:

(5)

设均值生成序列为:

Mb={mb(n)}={0.5xb(n)+0.5xb(n-1)},
(n=t-m+1,t-m+2,…,t)

(6)

在初始条件xb(1)=yb(1)下,累加生成序列的预测值为:

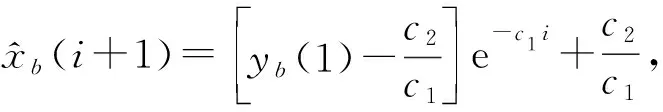
(7)

式中c1和c2可由下述公式求得:

(c1,c2)T=(DTD)-1DT(Yb)T,
(n=t-m+2,t-m+3,…,t)

(8)

D=(-Mb,I)T

(9)

I=(1,1,…,1)

(10)

由累减生成方法可求得t+1时刻的预测值为:

(11)

在t+1时刻,有B个数据,可构成序列:

(12)

t时刻xm的频率函数可表示为:

ft+1=ft+1(xm)

(13)

式中ft+1称为GBM(1,1)模型的概率密度函数。

2.2 GBM(1,1)模型的评估参数

(1) 估计真值X0

被测量在t时刻的估计真值可由瞬时加权真值表示:

(14)

式中:X0为用最大概率值表示的t时刻的最终解;Q表示将Xt+1分为Q组;q为第q组;xmq为第q组数据的中值;f(t+1)q为对应于xmq的灰自助概率。

(2) 估计区间[XL,XU]

给定置信概率为P,则t时刻被测量真值的估计区间可表示为:

[XL,XU]=[Xα/2,X1-α/2]

(15)

式中:a为显著性水平,a∈[0,1];置信概率P=1-a;XL、XU分别表示估计区间的下限值和上限值;Xa/2为概率是a/2时变量xm对应的值;X1-a/2为概率是1-a/2时变量xm对应的值。

(3) 动态不确定度U

t+1时刻被测量的动态不确定度可表示为:

U=XU-XL

(16)

(4) 区间估计可靠度PB

设测量过程中被测量的采样次数为T,若有h个数据位于估计区间[XL,XU]之外,则区间估计可靠度可表示为:

(17)

(5) 平均不确定度Umean

平均不确定度Umean是一个统计量,可以作为被测量随机性的评价指标。对平均不确定度Umean最理想的评价方法是在PB=100%的条件下,Umean取最小值。Umean越小,则被测量的波动范围越小。

为准确评价动态不确定度的估计效果,定义平均不确定度Umean为:

(18)

2.3 参数m,B,P的选取

由式(18)可知,平均不确定度Umean是m,B,P的函数,为使Umean获得最理想的评估结果,必须选择合适的参数m,B,P。由计算机仿真可得,在置信概率为99.7%的前提下,参数m,B与估计可靠度PB的关系如表1所示。

表1 参数m,B与估计可靠度PB的关系Tab.1 Relationship between the parameters m, B and the estimation reliability PB

由表1可知:若m值较大,则B的值也应当较大,算法的运算量也随之增大,由此导致跟踪被测量变化趋势的实时性减弱[11];若m值较小,则B也应选取较小值,因选取的数据量较小,估计结果的稳定性将会变差[12]。在实际问题中,需结合测量准确度要求和数据序列的样本量选择合适的m,B。在本文中,因数据序列的样本量较大且精度要求较高,应选取较大的m和B值。本文中选取m=7,B=1 000。

3 实 验

3.1 数据采集系统构建

密闭空间爆炸实验数据采集系统的基本结构如图1所示,主要包括K型热电偶温度传感器、信号调理模块、数据采集模块和采集控制主机等。所述数据采集模块选用Advantech PCI-1710数据采集卡,设定采样频率为1 kHz,选取爆炸零时后300 s的温度数据作为实验分析数据。

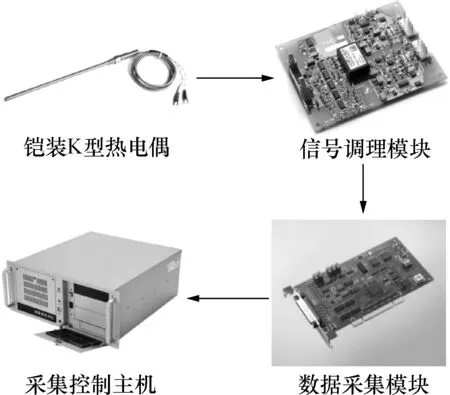
图1 数据采集系统基本结构Fig.1 Basic structure of data acquisition system

3.2 传感器选型

根据前期实验数据和传感器性能指标,选定铠装K型热电偶作为温度传感器,其基本性能指标为:温度测量范围0～1 250 ℃,准确度±2.2 ℃,响应时间0.73 s;实验所需传感器均经过计量检定,满足测量精度要求。

实验结束后,分别采用灰色模型GM(1,1)、Bootstrap方法和GBM(1,1)模型对测量所得数据进行真值估计,对比分析3种方法的真值估计结果。在给定置信概率为99%,95%,90%的前提下,分别采用Bootstrap方法和GBM(1,1)模型对测量所得数据进行区间估计,比较同一置信概率下2种方法的区间估计可靠度PB和平均不确定度Umean。

3.3 实验结果分析

3.3.1 真值估计

选取m=7,B=1 000,Q=10,图2(a)～图2(c)分别表示灰色模型GM(1,1)、Bootstrap方法和GBM(1,1)模型对爆炸温度的真值估计结果。图中相对时间是相对于实验起爆时间。

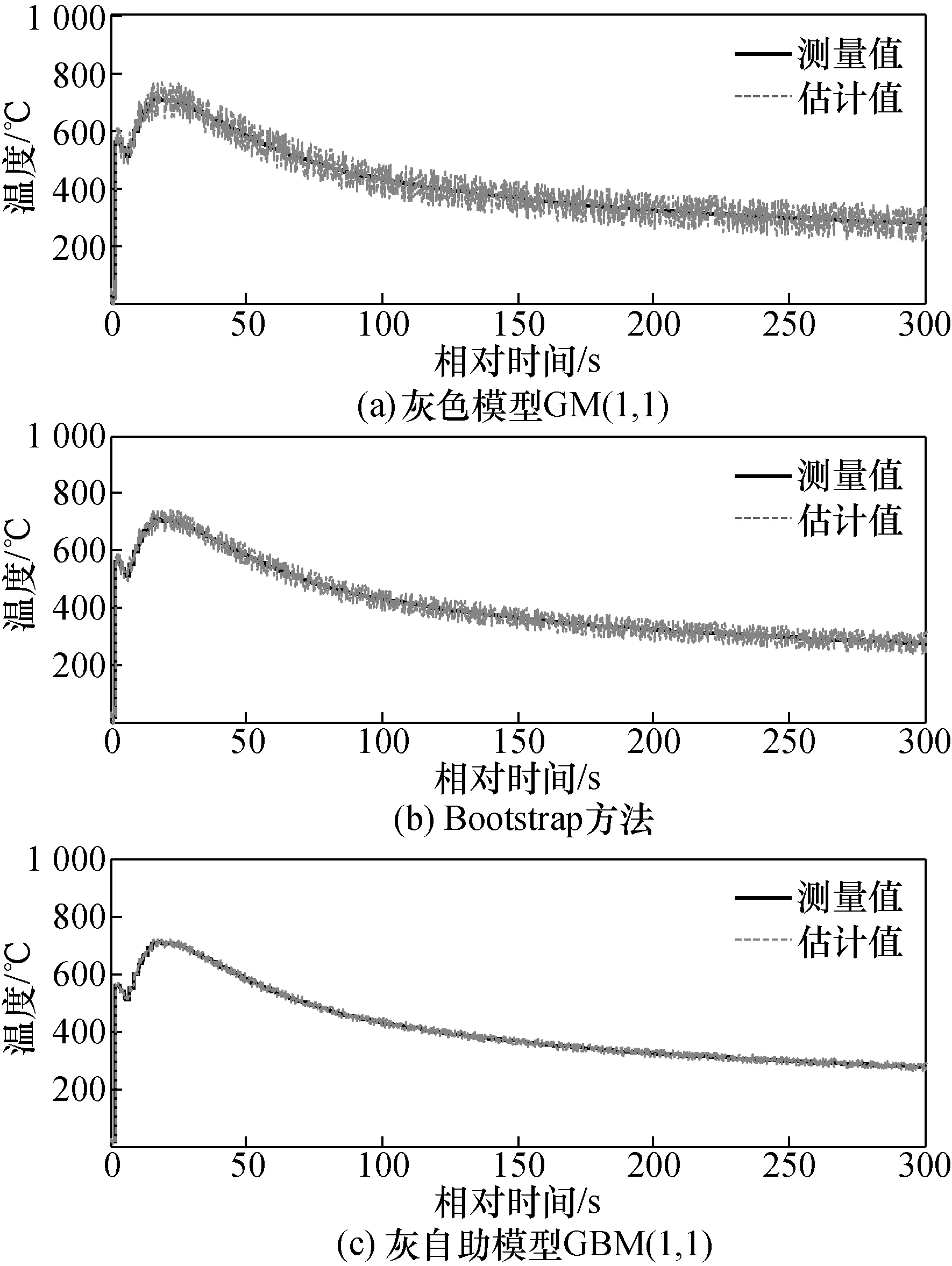
图2 3种模型的真值估计结果Fig.2 True value estimation results of the three methods

由图2可知,在密闭爆室温度参数的真值估计中,GBM(1,1)模型的真值估计结果优于Bootstrap方法和灰色模型GM(1,1)。分析认为,GBM(1,1)模型融合了灰色模型GM(1,1)和Bootstrap方法的优势,不仅具有对数据样本的扩展能力,而且具备对数据的预测机制,因此可以更加准确地模拟测量数据列的变化趋势。

为对上述3种模型的真值估计结果做出更直观的对比,对3种模型估计误差的分布区间、平均值、标准差和最大相对误差进行比较。首先,剔除估计值中的粗大误差,先用莱以特准则,以估计误差序列的3倍标准差为取舍标准,判定并剔除估计值中的粗大误差[13];其次,研究估计误差的分布规律,经验证,3种模型的估计误差均服从正态分布,其中GBM(1,1)模型估计误差的正态分布P-P图如图3所示。

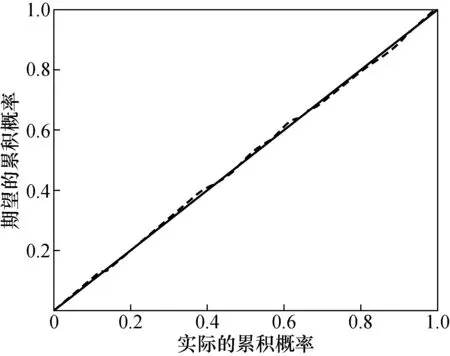
图3 GBM(1,1)模型估计误差的正态分布P-P图Fig.3 The P-P chart of normal distribution for estimation errors of GBM (1,1) model

3种模型估计误差的分布区间、平均值、标准差和最大相对误差的计算结果如表2所示:由于3种模型在各个采样点处的估计误差均近似服从正态分布,故其均值约为零;GBM(1,1)模型的估计误差分布区间、估计误差的标准差和最大相对误差均小于灰色模型GM(1,1)和Bootstrap方法,说明GBM(1,1)模型的估计误差较小,且具有较好的重复性和稳定性。因此认为GBM(1,1)模型的真值估计结果优于灰色模型GM(1,1)和Bootstrap方法。

表2 估计误差的分布区间和平均值Tab.2 Distribution interval and mean value of estimation error

3.3.2 区间估计

图4给出了不同置信概率下Bootstrap方法对爆室温度动态测量数据的区间估计结果(m=7,B=1 000,Q=10)。图5为对应置信概率下GBM(1,1)模型的区间估计结果,其中,图5(a)～图5(c)分别对应置信概率为99%,95%,90%。

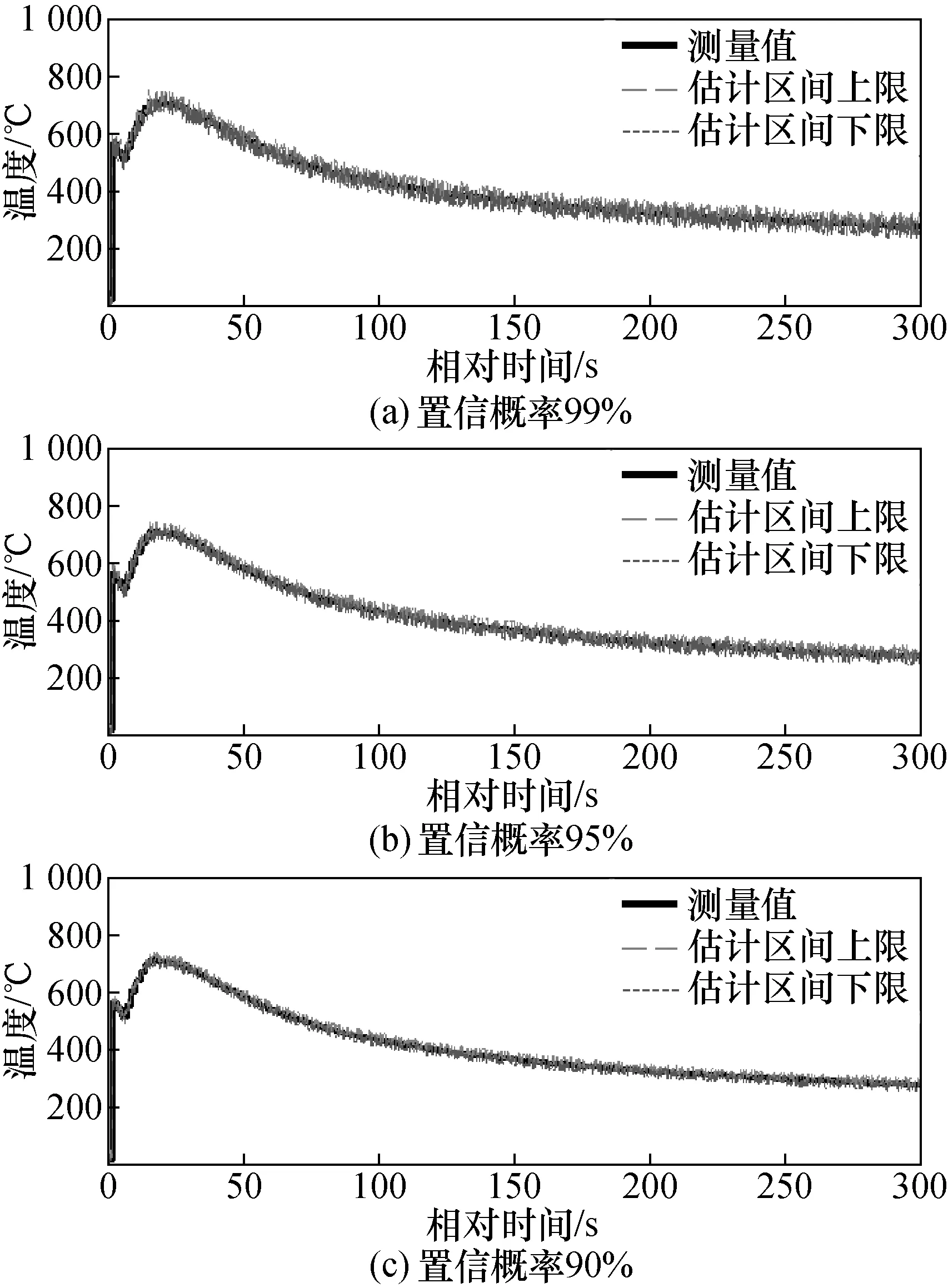
图4 不同置信概率下Bootstrap方法的估计区间Fig.4 Estimation interval of the Bootstrap method with different confidence levels

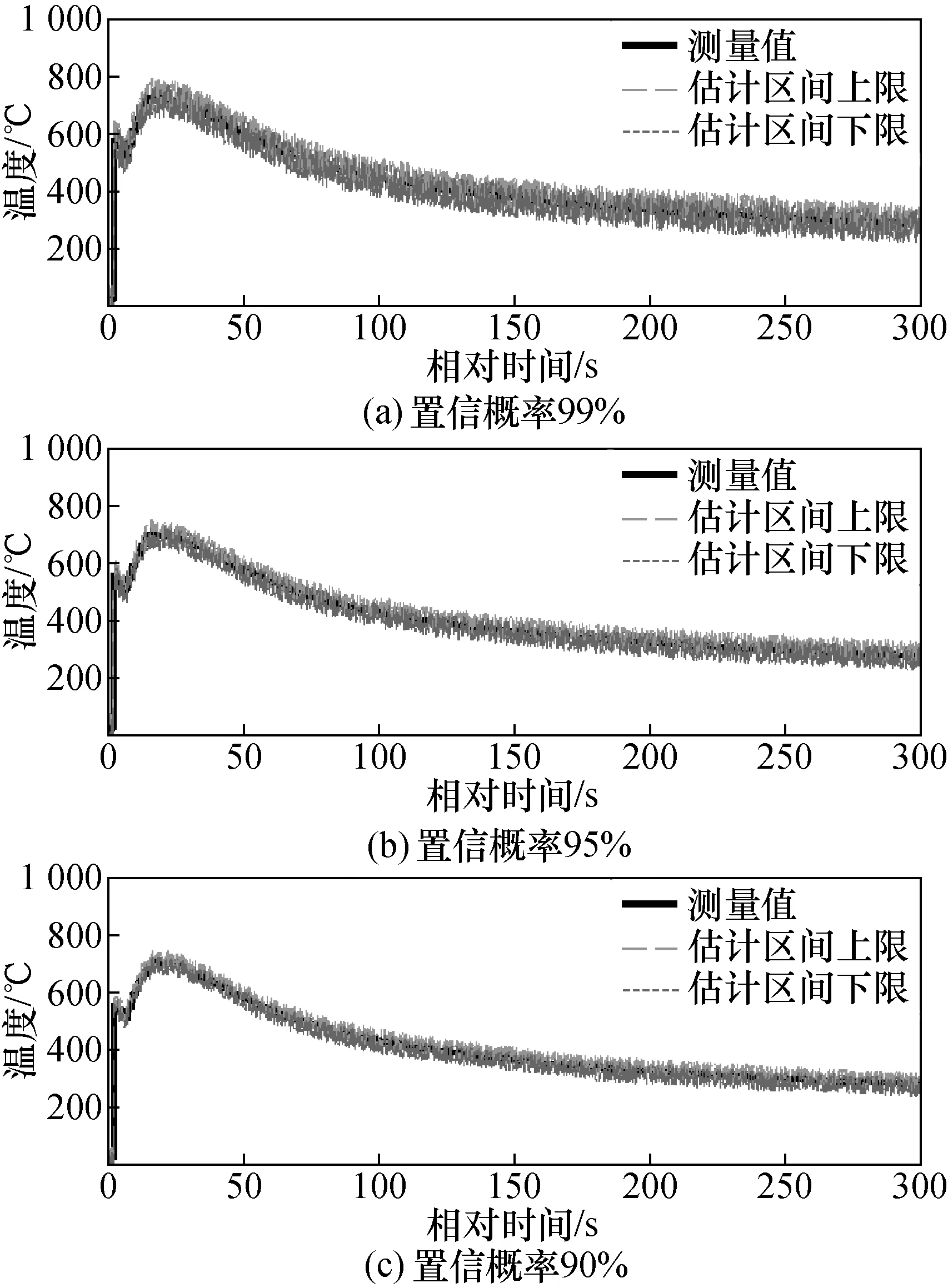
图5 不同置信概率下GBM(1,1)模型的估计区间Fig.5 Estimation interval of the GBM (1,1) model with different confidence levels

对比图4和图5可知,在相同置信概率下,GBM(1,1)模型的估计区间宽于Bootstrap方法,能够更加完整地包络被测量的动态波动范围。在置信概率不同的情况下,P越小,估计区间越窄,对被测量的动态波动范围包络越紧密,但区间估计的可靠度会随之降低。

为了更直观地对比Bootstrap方法和GBM(1,1)模型区间估计结果,表3列举了不同置信概率下2种方法的区间估计可靠度。由表可知:GBM(1,1)模型的区间估计可靠度高达90%以上,优于Bootstrap方法。

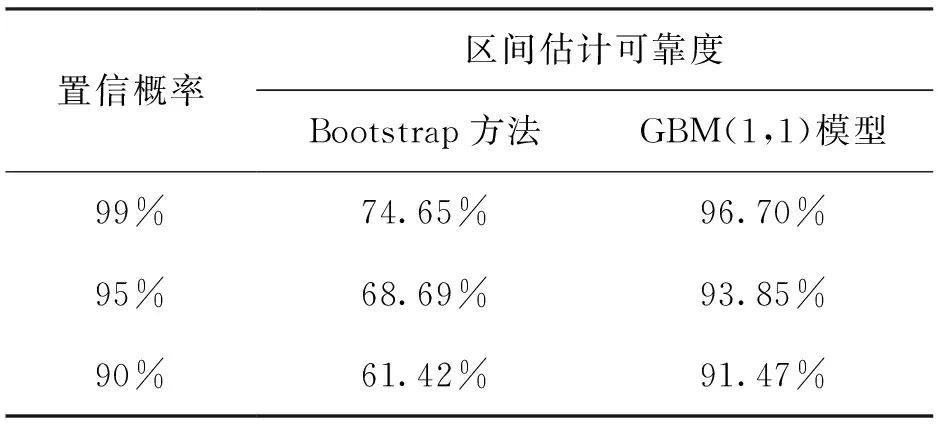
表3 区间估计可靠度比较Tab.3 Comparison rusult of the interval estimation reliability

3.3.3 动态不确定度

图6给出了不同置信概率下Bootstrap方法和GBM(1,1)模型对爆室温度动态测量结果的估计不确定度(m=7,B=1 000,Q=10)。

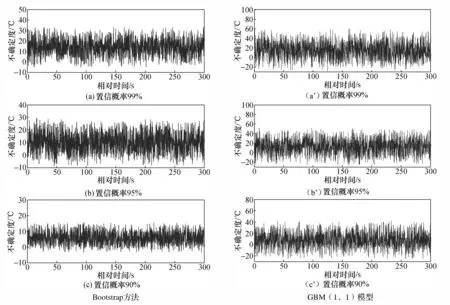
图6 不同置信概率下Bootstrap方法和GBM(1,1)模型的动态不确定度Fig.6 Dynamic uncertainties of the Bootstrap method and the GBM (1,1) model with different confidence levels

不同置信概率下Bootstrap方法和GBM(1,1)模型2种方法的平均不确定度如表4所示。由表可知,GBM(1,1)模型的平均不确定度略大于Bootstrap方法,且置信水平越高,平均不确定度越大。

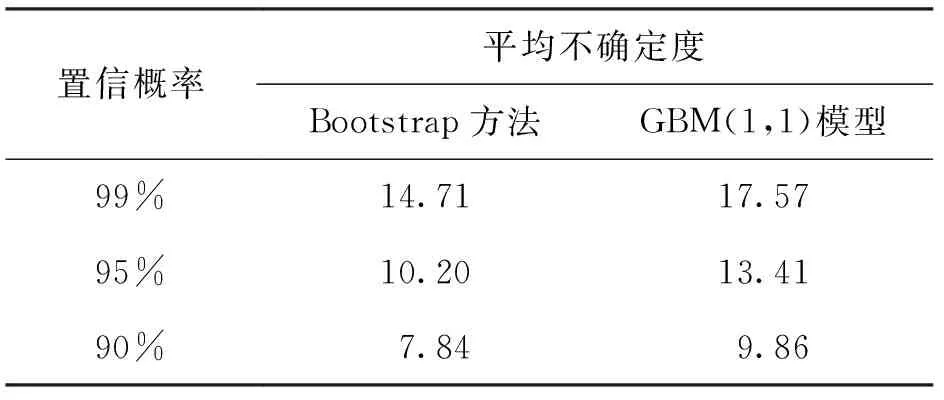
表4 平均不确定度比较Tab.4 The mean uncertainty comparison between Bootstrap method and GBM (1,1) model ℃

4 讨 论

本文运用灰自助模型GBM(1,1)对密闭空间爆炸实验中爆室气体温度动态测量数据序列的不确定性进行了研究,并选取一个基于统计特性的评估参数(平均不确定度)和3个动态评估参数(估计真值、估计区间、动态不确定度),对GBM(1,1)模型的评估结果进行了分析。

相比于灰色模型GM(1,1)和Bootstrap方法,GBM(1,1)模型包含了幂函数和线性回归的特性,改进了传统的差分模型和离散模型的缺陷,具有较强的趋势性,且累加生成有效减弱了原始测量数据的随机性误差。因此,GBM(1,1)模型表现出更加完善的预测机制,能够实现对被测量变化趋势的实时跟踪。

估计区间[XL,XU]描述了被测量的动态变化范围,随着置信概率P的增大,区间宽度逐渐增大,对被测量波动范围的包络越完整。平均不确定度Umean是被测量动态不确定度的均值,可以作为被测量随机性的评价指标。平均不确定度Umean最理想的评价方法为在区间估计可靠度PB=100%的条件下,Umean取最小值;但在实际问题中,难以实现PB=100%,因此需要选择合适的m和B,使PB尽可能趋近于100%。由表3可知,在m=7,B=1 000,Q=10的前提下,Bootstrap方法和GBM(1,1)模型的区间估计可靠度PB均无法达到100%,且Bootstrap方法的区间估计可靠度远低于GBM(1,1)模型,尽管其平均不确定度Umean小于GBM(1,1)模型,但综合考虑置信概率P和估计可靠度PB等参数,认为GBM(1,1)模型的动态不确定度评估效果优于Bootstrap方法。

5 结 论

爆炸过程的测量属于动态测量[14],本文将灰自助方法应用于密闭空间内爆炸气体温度的动态不确定度评估,构建了灰自助模型GBM(1,1),并通过估计真值、估计区间、估计可靠度、平均不确定度等参数验证了该模型对动态不确定度评定的有效性。GBM(1,1)模型融合了灰色模型GM(1,1)和Bootstrap方法的优势,可以在无任何先验信息的前提下准确模拟被测量的概率分布,并实时预测被测量瞬时值的变化趋势。相比于Bootstrap方法和灰色模型GM(1,1),灰自助模型GBM(1,1)具有更高的真值估计精度和区间估计可靠度,估计区间能够较为完整地包络被测量的动态变化范围。在密闭空间爆炸实验中,该方法能够对爆室温度的动态测量不确定度做出准确评定,具有较高的实用价值。