基于“可靠性”的自动分拣线维修模型
2020-08-07
(云南财经大学物流学院 云南 昆明 650221)
一、引言
随着经济全球化的深入,物流配送在各个领域得到了广泛的应用。分拣作为物流配送中心的环节之一,其整理速度和错误率的发生都影响到配送中心的效率和信用。自动分拣线在运行过程中,有发生故障的可能,这使得原本是为了提高分拣效率而存在的自动分拣线功能大打折扣,影响分拣线整体的运行节奏。
在物流中心总成本中,订单分拣成本约占总成本的百分之六十左右;在物流中心作业总时间中,订单分拣作业时间约占总时间百分之三十到百分之四十左右,无论是从成本角度还是时间角度,分拣作业无疑是物流中心运作的重要一环。而保证自动分拣线的可靠性、减少分拣线停机次数对提升物流中心整个作业活动有着重要的意义。
在贾照庆[1]的硕士学位论文中认为设备的可靠性从设计制造生产后即是确定的,通过预防性维修并不能提升设备的可靠性层次,最高只能维持或者达到设备的固有可靠性;侯超[2]基于时间延迟理论建立了基于维修费用—可靠性的同步维修模型和同步预防性维修模型,满足成本和可靠性的双重目标;夏正果[3]认为分拣机是配送中心设备运行最薄弱的环节之一,结合全员设备管理理论,提高员工设备管理的参与度,完善设备管理水平,减少设备失效时间;王舟[4]提出了对智能制造单元多设备系统进行联合设备监测的模型,在设备的可用度的限制下,建立了联合设备维修的预防性维修决策模型,实现了制造单元系统的总维修成本最小;金玉兰等[5]针对设备维修时间的随机性,建立等周期预防性维护策略,考虑维修时间不固定,以减少总成本;Nilda Tri Putri等[6]对机器预防性维修采用了一个新的模块化设计,有利于提高机器的可靠性和生产效率;S.Amiri等[7]提出了考虑预防性维修策略的能源枢纽调度问题的双目标数学模型;Kaican Kang等[8]考虑了预防性维修的灵活时间间隔和预防性维修的灵活时间间隔水平,提出了一种综合控制模型。
目前,大多数分拣线的维修模式是基于传统的预防性维修(Preventive Maintenance,PM)理论,本文结合上述观点,追求分拣线维修的可靠性目标,建立基于“可靠性”的同步维修模型。
二、自动分拣线作业流程、可靠性影响因素及同步维修思想
(一)作业流程
自动分拣线结构如图1所示:
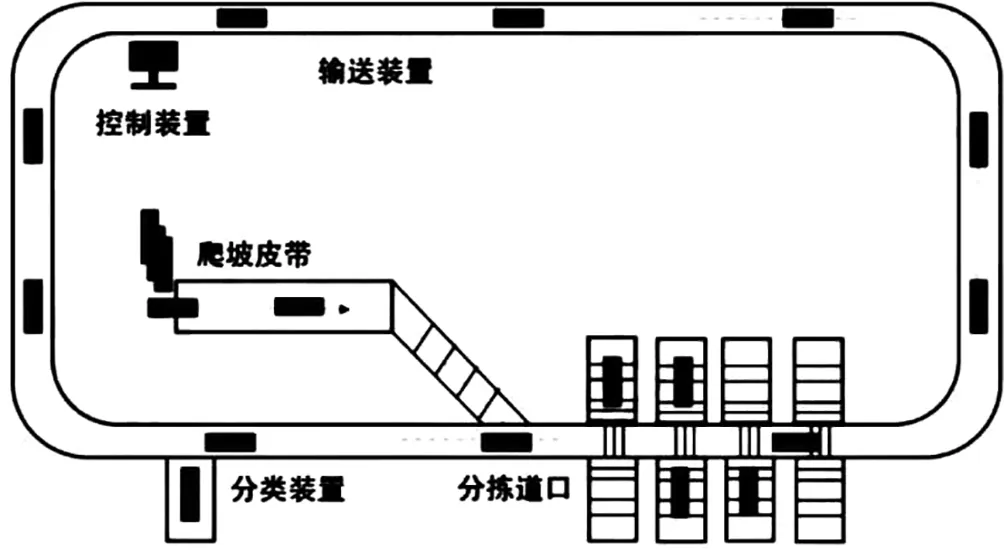
图1 自动分拣线结构图
自动分拣线的作业过程是,首先根据客户的订单确定交货时间,然后根据订单中物料的品类选择合适的拣取方式,在系统中规划物料分拣的路径,确定拣货路径,拣取物料,最后进行分类集中。如下图2所示:
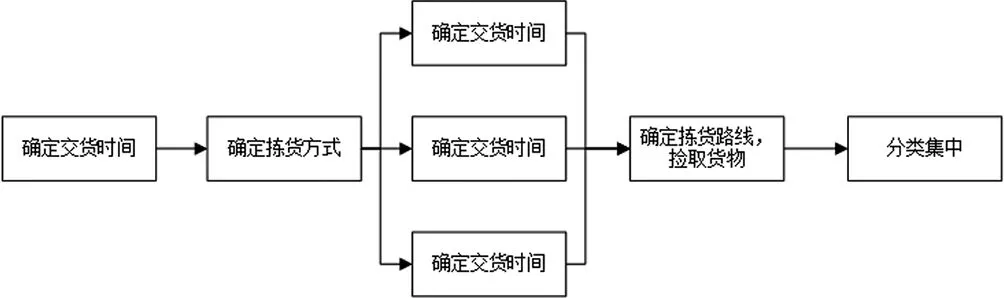
图2 自动分拣线作业流程图
(二)可靠性影响因素
设备的可靠性指标有许多,本文主要是指设备的可信度和出错概率。对自动分拣线上各设备进行可信度分析时,可信度和出错概率两个参数都可以从不同方面影响和评价分拣设备的可靠性,两者都能采集分拣设备在若干个时刻的瞬时运行状态,进行量化,形成数据,为制定分拣线维修计划提供支撑。
(1)可信度B(t)。设备在一个生命周期内,工作运行条件下,完成作业要求功能的概率。可靠度函数可用关于时间t的函数表示为:
B(t)=p(T>t)
(1)
根据可信度的定义可知,B(t)描述了设备在[0,t]时间内正常工作的概率,且B(0)=1,B(+∞)=0。
(2)出错概率
指正常工作尚在发挥功效的设备,在此时间点之后,单位时间内出现故障的概率。出错概率也是关于时间t的函数,记为F(t)。
F(t)=q(T>t)
(2)
F(t)=1-B(t)或F(t)+B(t)=1
(3)
其中,t表示规定的时间,T表示设备的生命周期。
对分拣设备的功能进行可信度和出错概率评估,找出分拣设备潜伏的故障问题,分析设备的可靠性,寻求分拣设备运行稳定、功能正常、提高设备可靠性的解决方法,为制定维修计划提供帮助。
(三)同步维修思想
同步维修思想主要应用于相互联系、相互影响却出现功能障碍,不能正常运行的多台设备,同步维修理论是依据80/20原则和大规模生产方式形成的。对于分拣线这样的复杂系统,由于分拣线各设备间相互关联、相互作用的特点,对各设备进行故障关联分析,从而做出多设备的维修决策。
分拣线上的各设备故障发生率差异很大,其对整条分拣线的停机影响亦不完全相同。现有的研究发现,大约有20%种设备故障占总停机时间的80%。鉴于此,针对出现高概率功能失效、长时间停转的这类设备的重点维修,能明显增加分拣线的使用效率。因此,建立分拣线可靠性模型、优化分拣线PM间隔期的关键在于,研究对象必须是对分拣线影响大、且占时长的20%的设备。
各分拣设备的PM间隔期的天数都不一致,如果分散每台设备进行维修,每进行一次维修,分拣线就会停转一次,停转时间不等,这将会对其日常工作造成巨大影响。如果按照“对分拣线故障隐患集中式处理”的理论,分组各分拣设备,每组包含多个PM间隔期相近的分拣设备,这样,可以明显减少分拣停机时间,提高分拣线工作效率。
三、基于可靠性的自动分拣线维修模型的建立及算法求解
基于同步维修思想,选择自动分拣线故障停机时间比较长的n台设备作为维修建模的对象,建立以可靠性为目标的同步维修决策模型。
(一)模型建立

(4)
为了确保设备累积故障概率低于设定的上限值Fmax,即Fi(Tb)≤Fmax(i=1,2,…,n),分拣线PM间隔期Tb必须满足:
Tb=min{Tbi}
(5)
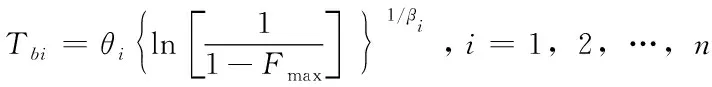
(6)
其中Tbi为可靠性Fmax约束条件下各设备的最大PM间隔期,Tb为优化前的分拣线PM间隔期。
要保证各设备的可靠性达到规定值,即Fi(Tb)≤Fmax,然后在此基础上,使分拣线PM间隔期内的Tb尽可能延长,以减少分拣线停机检修的次数。
(7)
其中,Tbi≥Tb·Yi,Yi∈Z+,Fi(Tb)≤Fmax,i=1,2,…,n
式中:
Yi表示Tbi/Tb比值取整,即
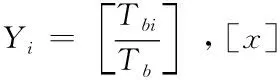
(8)
Tpmi为第i台设备的PM间隔期
Tpmi=Tb·Yi,i=1,2,…,n
(9)
Gi为第G台设备的PM活动次数
(10)
(二)算法求解
对所建立的模型进行求解,并提出以下算法,其主要步骤是,分拣线各设备按其最大PM间隔期的大小Tbi进行分组,制定各组设备优化维修计划Tpmi。具体算法步骤如下:
步骤1 对Fmax,θi和βi的初始值进行设定;
步骤2 运用式(5)和式(6),计算设定可靠性的前提下各设备的最大PM间隔期及分拣线PM间隔期;
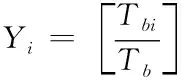
步骤4 依据各设备Tpmi大小的相似性,分组分拣线设备,制定每组设备的PM计划。
四、算例分析
某物流中心有一条自动分拣线经常发生故障,如何提高分拣线的可靠性便成为了企业尤为关注的问题。
基于收集分拣线大约3年的故障记录数据,根据80/20定律,调查分拣线上停机时间最长的6台分拣设备,其编号分别为M1,M2,M3,M4,M5,M6相应地,设备的相关参数如表1所示。
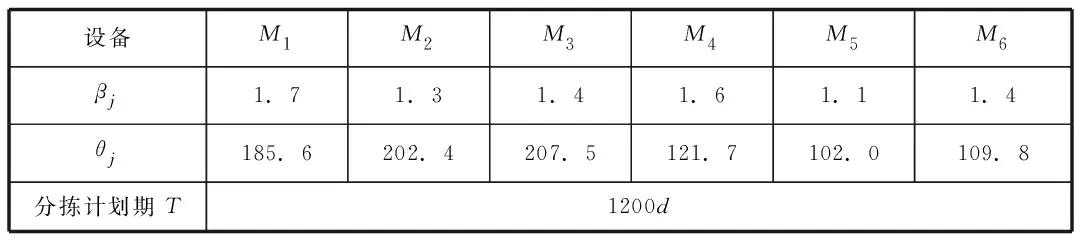
表1 分拣线设备相关参数
假定设备的可靠性要求Fmax=0.3,通过公式(5)和(6),得到Tb=40,利用公式(4)计算每台设备的累计故障概率,如表2所示。
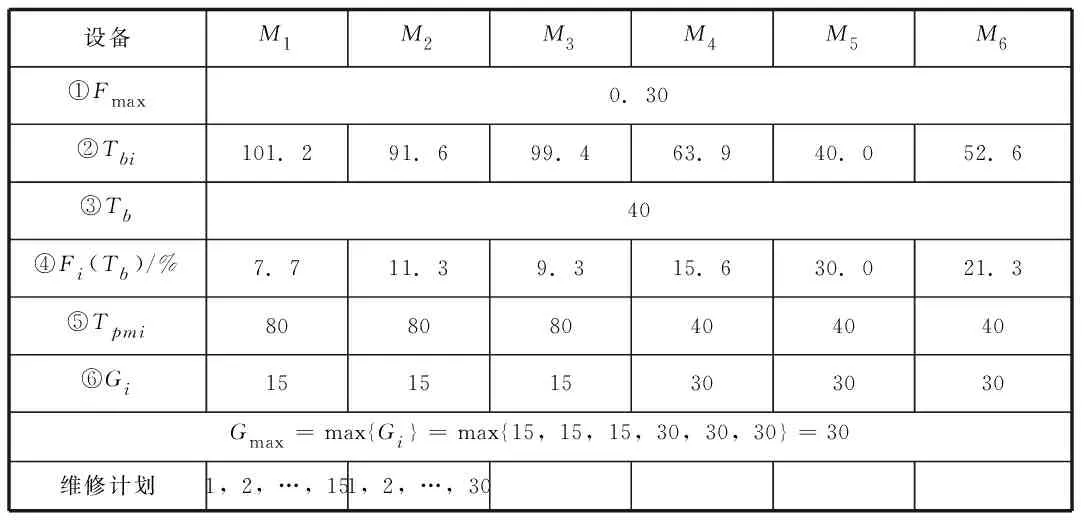
表2 模型计算结果及分拣线PM计划
从表2可以看出,满足分拣线Fmax=0.3要求的分拣线最大的PM间隔期为40d,否则设备M5无法满足其可靠性要求。值得注意的是,设备M1~M3满足Fmax=0.3可靠性要求的最大PM间隔期分别为101.2d,91.6d,99.4d,远远大于理论设置的最大的PM间隔期40d,且接近其两倍。若将M1,M2,M3这三台设备分为一组,则该组设备的最大PM间隔期则是80d,如此,既能够减少50%的PM次数,显著地减少分拣线停机次数和停机时间,又能够保障分拣线的可靠性,进而提高分拣效率。
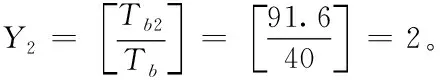
采用公式(10)计算计划期T内设备i实施PM活动的次数。例如,假定设备组M1~M3在1200d内共进行了1200/80=15次PM活动,;设备组M4~M6进行了30次PM活动,Nmax=30。
计算结果为Tb=30d,所有设备PM间隔期Tpmi是Tb=40的整数倍。但由于企业的维修计划一般是按月度、季度或年度制定的,所以该结果还难以在实践中应用。鉴于此,制定的分拣线PM计划时,有必要修正模型计算的结果。
若设定Tb=30d,相应地,各设备的PM间隔期如表4所示,把Tpmi代入公式(5),得到各设备的累计故障概率,如表3所示。因此,所有设备均达到了可靠性要求。
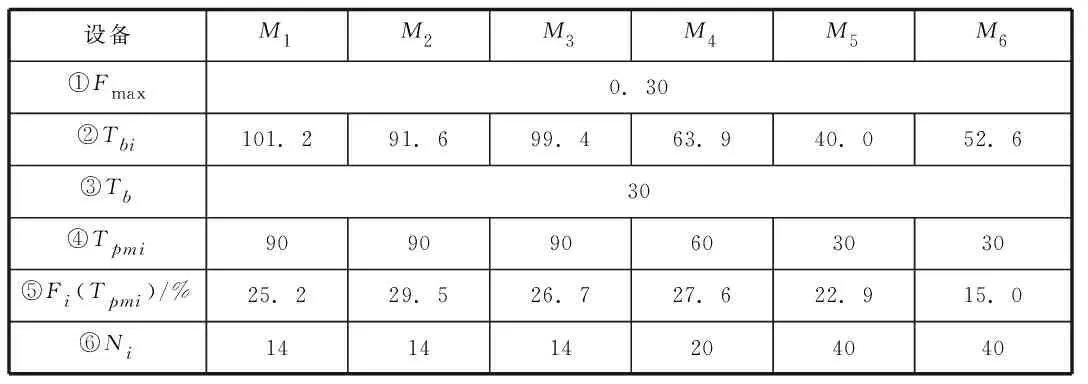
表3 修正后的分拣线PM计划
鉴于上述分析,我们制定的修正后的分拣线维修计划为:将M1~M3归为一组,按季度进行一次PM活动;把M4单独分为一组,相应地,这组设备的PM间隔期为2个月;M5和M6分为一组,按月进行一次PM活动。进过修正后的维修计划,如表4所示,不但保障了分拣线高的可靠性,而且更符合实际,进而使得应用性更强。
五、结语
分拣线维修管理作为提升物流中心分拣效率的重要途径之一,在理论研究及实践运用方面均都引起广泛关注。而自动分拣线相关设备的可靠性分析则是分拣线维修的重中之重。
本文基于同步维修、可靠性理论,针对自动分拣线的维修管理仍处于预防维修阶段,采用同步维修理论,建立了基于“可靠性”的同步维修模型,不但解决了分拣线可靠性低的问题,同时还减少了分拣线的部分维修费用。
本文所建立的维修模型,是依据设备PM间隔期的相近性,对设备进行分组,优化各组设备的PM间隔期,在满足和实现分拣设备可靠性要求的条件下,尽可能在一定程度上降低维修费用。鉴于物流中心一般采用月、季度、年度等来制定维修计划,修正了根据模型计算结果来制定分拣线维修计划模型。使得修正后的PM维修计划模型的实用性更强。
此外,鉴于本人研究水平有限,基于“可靠性”的自动分拣线的同步维修模型对分拣线的维修费用的降低仍处于理论探讨,其可靠性还需在实践运用中进行进一步的量化检验,希望在未来的研究中能有更加深入的分析。
