强激光辐照7075铝合金热响应与材料尺度律关系研究
2020-08-07李成龙邵俊峰郑长彬李雪雷
李成龙,汤 伟,邵俊峰,郑长彬,李雪雷,郭 劲
(1.中国科学院长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)
1 引 言
激光与物质相互作用研究的重点为材料对于激光激发的各种物理响应[1-2]。热响应是激光与物质相互作用过程中最重要的过程之一,通过适当调整不同的参数会出现不同的温升效率。一方面与激光的参数有关,如激光的波长、强度、光斑半径、辐照时间等,另一方面与被辐照样品本身的材料系数也有密切联系,如材料的成分组成和材料在升温过程中各种参数随温度的非线性变化。温升效应研究在国内外也是一项重要研究课题,王振宝研究了了均匀光斑和高斯光斑辐照下铝靶表面的温度分布[3]。马健和肖婧开展了脉冲激光与连续激光单独或联合作用下材料的温度仿真研究[4-5]。张翔宇研究了YSZ全陶瓷涂层对于激光辐照下的钛合金热响应的影响[6]。J.Osterholz研究了大光斑连续强激光辐照金属板的能量传递过程,得到表面产生蒸汽羽状物的激光功率密度阈值为3.4 kW/cm2[7]。Kyung-Cheol Lee通过测量激光穿透不锈钢时间,研究激光加热对于金属表面热传输特性的影响,测得了不锈钢表面对于激光的动态吸收系数[8]。
上述研究中,主要是以控制激光参数变化和变换涂层材料来研究金属板的热响应为主。现实条件下,由于受试验设备、实验耗费和实验场地等条件的限制,许多实验无法在原尺寸模型下开展。因此开展尺度律的研究,陈发良和余同希开展结构热力响应及失效的尺度律的研究,理论分析了被辐照目标热力响应的缩比关系[9],但未开展数值仿真和实验加以验证。本文采用数值模拟与实验相结合的方法,研究了不同尺度律下的7075铝合金模型在等效时间内,被波长为1064 nm的连续激光辐照下的热响应,来讨论材料尺度律与温升速率之间的关系。
2 理论模型
激光辐照到靶材的表面,靶材吸收激光能量转换为热能向材料内部传播,引起内部的温度变化。假设原型和模型中靶材材料相同且为各向同性,那么在直角坐标系下,模型靶材内部瞬态温度场θ(x,t)分布为傅里叶热传导微分方程:

(1)
而原型靶材上的温度场为θ(x,t)为:

(2)
模型与原型几何相似,但是热传导问题与力学响应不能同时满足几何相似律。所以这里单讨论材料的热响应缩比规律[9]。对(1)、(2)两式,按缩比规律[10]则有:
(3)
其中,λ为几何相似因子;x、t、γ、q、X、T、Γ、Q分别表示模型和原型上的长度、时间、面源和体源项。
初始条件和边界条件为:
θ|t=0=300 K
(4)
(5)
式中,ρ、CP、k、h、α分别为材料的密度、比热容、热传导系数、表面传热系数和表面吸收系数,以上材料参数不随尺度律发生变化;θ、t、I分别为靶材内部分布的温度场、热量传输时间和入射激光功率密度;∑1和∑2分别为受光面和背光面。
3 数值模拟
利用有限元软件COMSOL对激光辐照7075铝合金进行数值建模,仿真模型如图1所示。强激光垂直入射到金属板表面,金属板固定在夹具之中。强激光入射到金属板表面之后,金属板吸收激光转化成热能在表面及内部传输,引起表面及内部的温度升高。
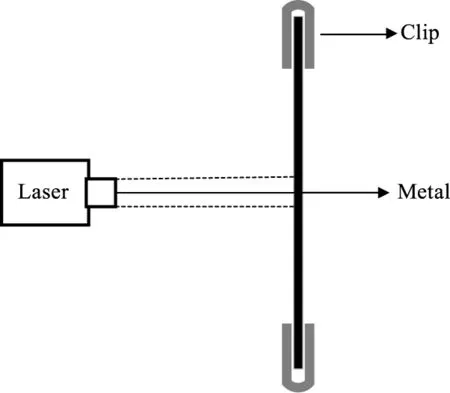
图1 强激光辐照等效仿真模型
3.1 热源的施加
金属表面对激光的吸收作用距离为0.1~5 μm,因此模型中将连续高斯光束等效成材料表面的面热源向材料内部传输热量,较好的模拟了激光对材料的加热现象。在COMSOL中在表面添加面热通量来实现热源的分布,在材料表面的光斑区域将热源设置成高斯分布,那么材料表面吸收的激光功率密度也就是热源分布可以表示为:
(6)
式中,P为作用激光的功率;光斑半径为r;α为材料表面对激光的吸收率。
3.2 材料参数选取
利用COMSOL建立数值模型分析铝合金板内部温度分布时,还要考虑铝合金板的各项物理参数的非线性特性。主要用到的热物理参数有:比热容、密度、导热系数以及金属对激光的吸收率。金属吸收率一般来说会随温度升高而增大,特别是在熔点附近出现大幅度上升。但本模型讨论过程为金属发生熔融之前的温升过程,对于1064 nm的激光,根据Hagen-Rubens公式,吸收率在熔点之前变化不大,所以取为定值。表1给出在仿真模型中材料热物理参数的设置。设置铝合金板和环境初始温度为300 K,对流换热系数为10 W/(m2·K)。
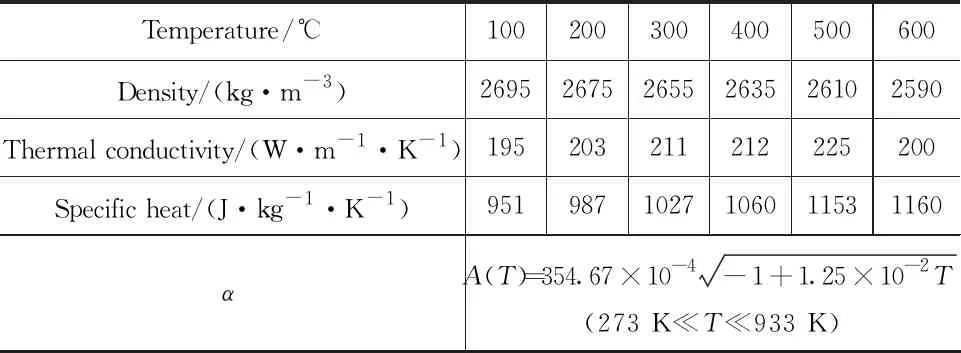
表1 铝合金板热物理参数
4 仿真结果分析
4.1 仿真参数
在COMSOL中开展模型仿真计算,沿着Z方向垂直射入铝合金表面,辐照在铝合金表面。激光和铝板具体参数由表2给出,表中P为激光功率;d为光斑直径;D为功率密度;A为铝板边长;L为铝板厚度;t为辐照时间;λ表示模型与原型之间的相似因子。

表2 仿真模型参数
4.2 仿真结果及讨论
为了验证数值模型的有效性,按照公式(1)和(2),仿真时的边界条件设置为除辐照面其余面为绝热条件,观察不同尺度律材料内部的温度场随时间的分布。仿真结果如图2所示。

图2 无对流和辐射下铝板中心仿真温度
图2为各尺度律下铝板辐照中心点温度随时间变化情况。由图可知,在没有对流换热和热辐射边界条件下,原型与各模型辐照中心点的温度值相等,温升速率一致。从而验证了缩比方法是可以应用材料的热响应问题上的,与理论吻合。同时也证明仿真过程中采用的模型是合理的,即可以利用仿真模型得到超出实验室条件以外的实验结果。下面考虑实际实验环境,将被辐照靶材与周围环境的自然对流换热和热辐射的边界条件加入仿真数值模型中。图3为尺度律λ=1的模型在辐照时间为150 s时的表面温度场分布云图。图4给出了不同尺度律λ下铝板温度随时间变化的数值模拟结果。

图3 样品表面温度场分布云图
从图4中可以看出,在加入自然对流换热和热辐射的边界条件之后,各尺度律下铝板温度分布情况出现差异:温升速率和最高温度都因尺度律的变化而改变。在等效时间内,尺度律λ越小的铝板升温速率越快,最终中心点达到的温度越高;尺度律λ差值越大,温升速率和最终温度差值越大,其中λ=1和λ=0.5两个模型最终温度差值达到143.2 ℃。对比图2数据,对于温升过程中各模型出现的温度差异,分析认为主要是来源于自然对流换热产生的热量差异。因对流换热过程中的热量流失与靶材的表面积正相关,尺度律λ越小的铝板对流换热损失的热量相对于尺度律λ大的铝板要小,所以导致最终温度较高,温升较快。
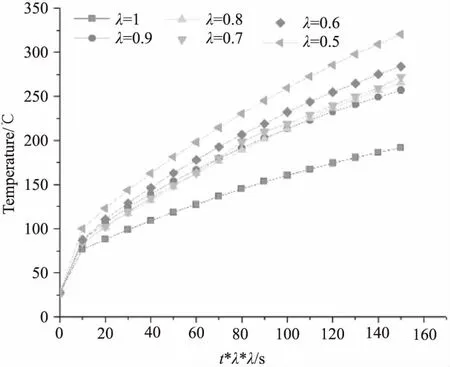
图4 加入对流和辐射下铝板中心仿真温度
在激光辐照面选取四个点查看铝板整体温度分布情况,分别为中心点A,沿x轴距离λr点B,距离2λr点C,距离3λr点D。各尺度律下铝板四点温度分布数值模拟结果如图5所示。由图5可知,在各尺度律铝板中,除去自然对流换热引起的温度的差异,各模型四点温度速率相同。并且随着距离的增大热量的传输速率变慢。
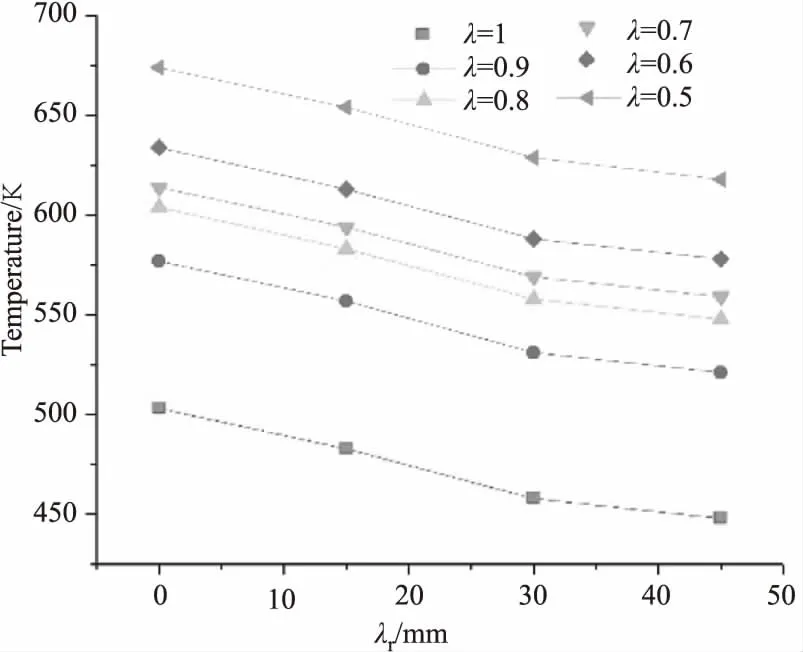
图5 各尺度律铝板中ABCD四点仿真温度
5 实验验证
5.1 实验系统
为了进一步验证各尺度律模型的正确性,搭建了一套实验平台,按照表2中的模型参数开展温升试验。实验系统如图6所示。其中,红外热像仪型号为FLIR T360 s便携式热像仪,如图7(a)所示,像素640×480,热灵敏度为30 mK,测量温度精度为±2 ℃;激光器采用型号为HF-1000的光纤激光器,如图7(b)所示,出射连续波长为(1.06±0.02)μm,可实现0~2000 W激光输出。高功率激光器经过聚焦光学系统后,垂直辐照在铝板上;红外热像仪置于铝合金板后方,实时监测铝板后表面的温度变化;楔形镜用于分光,将一定比例的光分给光功率计,对激光器的出射激光功率进行实时监测。在每次实验之前,用另一个功率计与激光光斑尺寸进行标定;实验开始时,触发激光器的同时打开红外热像仪对铝板进行温度监测。
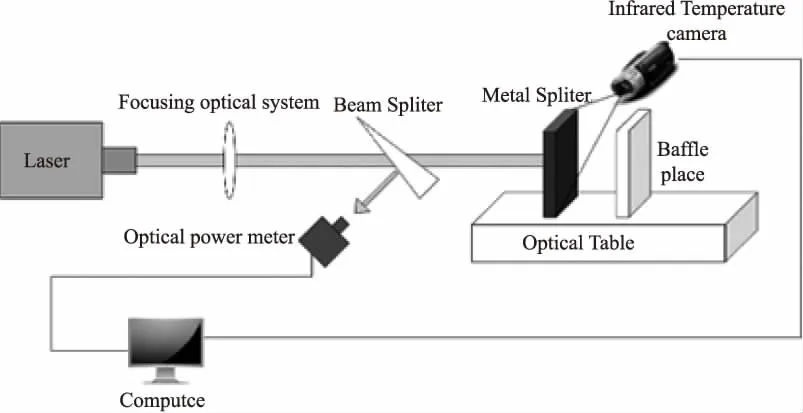
图6 实验原理图

图7 红外热像仪和光纤激光器
5.2 实验与数值结果对比
图8给出各尺度律下铝板中数值仿真温度与实验实测温度对比曲线。图9为通过实验得到不同尺度律样品的温升曲线对比。
对比图8中各模型数值模拟结果和实验测量结果可以看出,除了λ=1模型中前30 s区域以外,实验测量结果温度值均低于数值模拟温度值。最终各尺度律温度差值分别为39.1 ℃、26.2 ℃、38.3 ℃、52.2 ℃、50.8 ℃、53.5 ℃;相对误差分别为16.5 %、13.4 %、12.5 %、16.6 %、15.1 %、14.3 %。分析认为差值主要由两方面造成:一是在数值模型中材料系数与实验样品存在误差;二是实验室中存在的排风系统的影响,排风系统会增加铝板与空气的强制对流换热,因此热量损耗较大,导致实测温度小于数值仿真温度值。
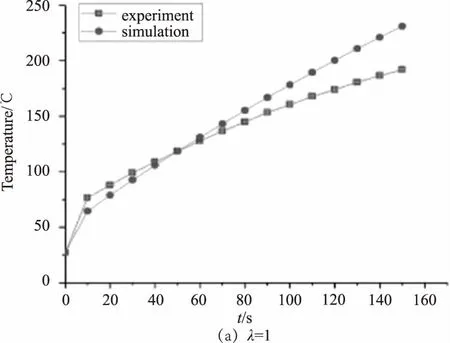
图8 各尺度律下仿真与实验温度对比
图9中实测铝板温度分布与数值模拟结果分布相似:尺度律λ越小的模型最终中心点的温度越高;模型间尺度律λ相差越大最终温度相差越大。但是由于实际铝板材料成份的差别,温度差值不如数值模型中分布均匀。实验中λ=1和λ=0.5两模型实测温度相差128.2 ℃,小于于仿真时温度差143.1 ℃。

图9 不同尺度律铝板实测温度
6 结 论
本文对7075铝合金板在强激光辐照下产生的热响应与材料尺度律关系进行实验和数值模拟研究。研究结果表明:
(1)在等效时间内,无对流和热辐射条件下,各尺度律下铝合金板温度分布相同,数值模型与理论符合度较好。
(2)考虑热对流和热辐射条件下,各尺度律铝合金板温度分布出现差异,满足尺度律越小最终温度越高的规律。分析认为对流换热占主要影响因素。
此方法可以预测尺寸较大的原型实验中的温度分布,具有一定的应用背景和实用价值。
