一种基于MATLAB的碎屑岩粒度分析方法
2020-08-07方梦阳何建宁王万虎李明哲
方梦阳,何建宁,王万虎,李明哲
(中国地质调查局 海口海洋地质调查中心,海南 海口 570100)
利用粒度数据对沉积物进行粒度分析,能有效地判定沉积物搬运方式,判断介质动力条件,区分沉积类型,研究沉积物的成因机制和古气候(谢远云等,2002),因此对碎屑岩的粒度进行精确而有效的统计很有必要。然而,筛析和沉降等传统粒度测量方法非常耗时,且统计方法不一样,结果有一定的偏差,因此需要一种新的方法来完成粒度测量(Friedman,1958)。目前使用较广的有激光粒度分析法及薄片粒度图像分析法。前者对于砂泥、黏土等胶结较差的样品有较好的应用效果,而对于胶结程度中等及以上的砂岩和粗粉砂岩样品,地质工作者一般使用薄片粒度图像分析法来进行粒度分析(陈建强等,2004)。当前所使用的薄片粒度分析方法需手动测量各个颗粒的直径,再统计薄片的粒度分布,工作繁琐,即使获取粒度分析结果后,绘制粒度曲线及计算各类粒度参数仍然费时费力(袁瑞等,2015)。
为解决以上问题,改进显微薄片粒度分析法,许多学者将计算机图形图像学引进到粒度分析中,如张学丰等(2009)应用Photoshop定量分析了川东北三叠系碳酸盐岩岩石结构参数,Andriani和Walsh(2002)运用美国德州大学开发的UTH-SCSA图形工具软件研究了沉积岩的气孔结构和颗粒分布,季长军等(2012)利用ImageJ软件对碎屑岩薄片进行图像处理也取得了一定的效果。但是,以上方法所使用的软件多为非开源的商业软件,不能根据图像类型及时调整处理过程参数,结果多不甚理想。
MATLAB是美国MathWorks公司出品的商业数学软件,主要应用于图像处理及数值计算等方面。通过MATLAB可以对碎屑岩薄片图像进行图像处理、目标测量、数据处理等操作。MATLAB语言作为一种基于C语言的高级技术计算语言,可高效完成碎屑岩粒度分析中的一系列工序,有效解决传统薄片粒度图像分析方法所存在的问题(Paterson and Heslop,2015;Aligholietal.,2015)。
本文细粒长石石英砂岩样品采集于广东省清远地区清新县龙须带水库上三叠统小云雾山组二段(T3xy2),将其偏光显微镜下薄片图像作为研究对象。小云雾山组二段由较细的碎屑岩组成,水平层理、交错层理发育,层面平整,发育冲刷面,中部发育水下河道沉积层序,细粒石英质砾岩常以透镜体形式产出,岩层整体含钙质较高,见细粒砾质长石石英砂岩,含腕足类化石,局部见劣质煤层,这些特征反映当时的沉积环境为浅湖相及河湖交互相(陈凯等,2018)。
1 MATLAB图像处理原理
MATLAB图像处理的基本思路为,通过对原始镜下薄片图像进行灰度化、二值化、图像增强、形态学处理等图像处理工作,将原始图像中干扰信息去除,准确保留、突出图像中碎屑颗粒轮廓或边界,确保后续颗粒粒度数据测量结果精确可靠。
1.1 导入图像
一幅数字图像在MATLAB中可以表达为矩阵:

矩阵中每一元素均对应数字图像中的一个像素,f(M,N)的值为图像在该点的亮度。使用imread函数将图像读入MATLAB环境(MATLAB版本为R2013b),具体命令如下:
A=imread(‘grain.tif’);%A为矩阵名,grain.tif为显微镜下采集到的碎屑岩单偏光图像文件名
利用CCD(电荷耦合图像传感器)所采集到的碎屑岩单偏光下颗粒图像(放大倍数为10×5,如图1所示)便通过imread函数存储到矩阵A中。

图1 原始镜下图像Fig.1 The original microscopic image
1.2 图像灰度化及二值化
因CCD所采集的颗粒图像为RGB图像,而粒度测量工作主要目的为识别图像中每一颗粒的形态学要素,并不关心岩石颗粒的类型,故需通过灰度化使图像去除不相干信息,使RGB图像变为灰度图像。具体命令为:
A1=rgb2gray(A);%灰度化
为便于计算机自动对图像进行分析,需将获取的灰度图像进行二值化处理,尽可能将干扰计算机判断的因素减少。图像的二值化处理就是将图像上点的灰度值设定为0或255,也就是将整个图像呈现出明显的黑白效果,即将256个亮度等级的灰度图像通过适当的阈值选取而获得仍然可以反映图像整体和局部特征的二值化图像(Gonzalezetal.,2013)。因此,选取合适的阈值是二值化效果好坏的关键。
本文所采用的最大类间方差法OTSU法(Otsu ,1979)是一种自适应阈值选取的方法,它是按图像的灰度特性,将图像分成背景和目标两部分。背景和目标之间的类间方差越大,说明构成图像的两部分的差别越大,当部分目标错分为背景或部分背景错分为目标都会导致两部分差别变小。类间方差最大的分割意味着错分概率最小,是一种非常优秀的确定二值化阈值的方法。具体命令如下:
Level=graythresh(A1);%最大类间方差法获取二值化的阈值
A2=im2bw(A1,level);%二值化
经灰度化及二值化处理后的颗粒图像如图2所示。通过对碎屑岩图像进行灰度化及二值化处理,处理后图像噪点较少,整体亮度合适,颗粒轮廓明显。

图2 二值化后图像Fig.2 The binary microscopic image
1.3 图像增强及形态学处理
上述处理所获得的二值化图像中仍有较多黑点,黑点为碎屑岩胶结物中杂基或微小的碎屑颗粒,在图像学中可将其类比为一种随机噪声。通过构建一个自适应中值滤波器可有效地去除噪声,改进图像显示质量,便于后续处理。
A3=adpmedian(A2,7);%自适应中值滤波
经自适应中值滤波处理后的图像如图3。由图3可知,adpmedian函数虽去除了较大部分的噪声,但在岩石颗粒表面及胶结物中仍有部分微小碎屑充填。对于后续统计工作,这些充填在胶结物中或散布在颗粒表面的微小碎屑会影响统计结果。受制于图片像素分辨率,计算机无法分辨颗粒粒径小于15 μm(尺寸换算前为20像素)的颗粒,因此将粒径小于15 μm的颗粒统一按照胶结物处理。

图3 自适应滤波后图像Fig.3 The adaptive filtering microscopic image
中值滤波处理后图像经过形态学腐蚀及膨胀操作,可以最大程度保留统计碎屑颗粒的原始形态学要素。形态学开运算中,腐蚀会去除较小的对象,而随后的膨胀操作会还原所保留对象的形状。具体命令如下:
A4=imopen(A3,strel(‘disk’,20));%一次开运算,掩模为20像素直径圆盘
A5=imfill(A4,‘holes’)
图像处理结果见图4所示。处理后图像较好地还原了原始薄片图像中颗粒的形状,颗粒内部光滑均一,颗粒边缘明显平滑,毛刺减少,颗粒间隙更为明显,无假连接区域。处理后图像能很好地被计算机识别。

图4 形态学处理后图像Fig.4 The morphological processing microscopic image
1.4 时效及精度对比
本研究主要针对碎屑岩粒度分析,而激光粒度分析法主要适用于胶结程度中等及以下的岩石,因此本节仅对比薄片粒度图像分析法与基于MATLAB粒度分析法。
时效性方面,通过统计同一薄片经两种不同方法测量获得所有颗粒粒径数据所用时长。结果显示,薄片粒度分析法共耗时56 min,基于MATLAB的粒度分析法共耗时72 s。基于MATLAB的粒度分析法较薄片粒度分析法耗时大大减少。
精确性方面,通过手工勾绘颗粒边界,计算颗粒粒径作为标准粒径,选用同一颗粒标准粒径对比两种方法所得粒径数据精度。结果显示,薄片粒度分析法平均误差小于215 μm,基于MATLAB的粒度分析法平均误差小于73 μm,表明基于MATLAB的粒度分析法较薄片粒度分析法精度有较大提升。
2 MATLAB统计计算
MATLAB统计计算的基本思路为,通过对前述图像进行统计获取各颗粒形态学参数,利用所得的颗粒粒度数据计算颗粒的粒度参数,进而运用萨胡公式等沉积环境判别公式进行沉积环境判断。
马少华等[13]首先制备出了双十八烷氧基二硫代磷酸吡啶盐(PyDDP-18)作为表面活性剂,并以其作为硫源,以钼酸铵作为钼源,通过共沉淀法制备出了表面修饰有PyDDP的MoS2纳米微粒,该种微粒具有较好的油溶性及优异的耐磨润滑性能。
2.1 获取颗粒形态学参数
颗粒的形态学参数集合包括其各类形态学参数,如最大粒径、颗粒重心坐标、颗粒周长及最小外接矩形等,其中传统镜下测量方法仅能粗略测量最大粒径,其余均不能测量。
regionprops函数是MATLAB自带的IPT(图像处理工具箱)中用于计算区域描绘子的主要工具。通过该函数,可以有效获取碎屑颗粒的最大直径、周长、重心位置、面积等各类形态学参数。具体命令为:
[labeled,numObject] = bwlabel(A5,4);%统计数目
rgb_label=label2rgb(labeled,@spring,‘c’,‘shuffle’);%着色统计颗粒
graindata=regionprops(labeled,‘all’);%存放结果
所有参与统计的颗粒均被标注及着色,标注图像如图5所示。参与统计颗粒的各类形态学参数数据存放在名为graindata的表格中,参数单位为像素数。
依据Friedman(1962)提出的粒度回归校正方程将矩阵中最大直径d换算为筛析颗粒直径D,然后通过Krumbein提出的对数换算公式(Krumbein,1934)即可获得最终各颗粒的真实粒径φ值。本文共统计得到颗粒数211颗,按照0.25φ为统计区间,划分φ值粒级结果如表1。

图5 标注图像Fig.5 The marking microscopic image

表1 薄片粒度统计结果Table 1 The statistics of slice size
2.2 计算粒度参数
常见的粒度参数有平均粒度(Mz)、标准偏差(Sd)、偏度(Sk)和峰度(Kg)。平均粒度(Mz)表示一个样品的平均颗粒大小,反映搬运介质的平均动能;标准偏差(Sd)代表颗粒的分选程度,反映颗粒的分散和集中状态;偏度(Sk)是用来表达频率曲线对称性的参数,不同沉积环境形成的沉积物频率曲线的形态不同,频率曲线的偏度对了解沉积物成因有一定的意义;峰度(Kg)用来在与正态频率曲线相对比时,说明曲线的尖锐或钝圆程度。

式中fi为各粒级组的频率百分数,xi为各粒级组的中值。
上述两种方法中,矩阵法较图解法更为精确,但依然存在以粒级分组代替某一颗粒数据的现象,导致计算结果仍然无法反映最精确的粒度分析结果。因此,本文引入直接计算法改善上述两类方法所存在的精度缺陷。直接计算法不需要将各粒度数据进行粒级分组,直接使用每一颗粒的粒度数据,依据统计学中对平均粒度、分选系数、偏度、峰度的定义,使所有颗粒数据均参与粒度参数计算,所得结果最为准确。计算各粒度参数的准确公式为:

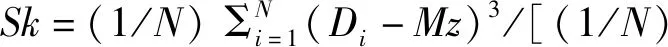
式中Di为第i点的真实粒径,N为颗粒总数目。
在MATLAB中可快速利用直接计算法公式求得各项粒度参数值,MATLAB命令如下,其中D为换算后真实粒径所存储的数组:
Mz=mean(D);%平均粒度
Sd=std(D);%标准偏差
Sk=skewness(D);%偏度
Kg=kurtosis(D);%峰度
经计算,矩阵法所得粒度参数结果为:Mz=2.783 8,Sd=0.889 5,Sk=0.591 5,Kg=3.547 0;直接计算法所得粒度参数结果为:Mz=2.776 0,Sd=0.885 4,Sk=0.439 6,Kg=2.238 6。依据矩阵法定义,仅取每个粒级区间中值参与计算,矩阵法参与计算颗粒为15颗。直接计算法中所有被识别颗粒均参与计算,直接计算法参与计算颗粒为211颗。以直接计算法所得结果为基准,矩阵法所得结果中平均粒度Mz偏离0.28%,分选系数Sd值偏离0.46%,偏态值Sk偏离34.55%,峰态值Kg偏离58.45%。
计算结果表明,平均粒度Mz及分选系数Sd的计算结果均十分接近,计算方法可以互相替换;矩阵法所得偏态值Sk、峰态值Kg与直接计算法所得值差别很大,没有明显的相关性,不可相互换算。
参与计算颗粒数目与计算结果的准确性呈正相关。Mc Manus在当时的测量条件下,无法获取所有颗粒的粒度值使之参与运算,因此,其矩阵法计算公式存在一定的局限性。直接计算法依靠数字图像处理技术,参与计算的颗粒数目比矩阵法多,计算结果精度较矩阵法有大幅提升。
2.3 判断沉积环境
当前对沉积环境判断多运用萨胡公式(Sahu,1965)。萨胡公式是Sahu于1965年在碎屑岩沉积物研究中提出的一种判断沉积环境的公式。该判别函数是根据现代沉积物提出的,故对碎屑岩环境分析存在局限性(赵澄林等,2000)。Sahu根据河道、泛滥平原、三角洲、海滩、风坪、风成沙丘、浅滩及浊流沉积物的粒度分析结果,利用线性多元判别公式,得出4个综合公式(表2),用以区别上述沉积物沉积环境。
另外,李昌志等(1999)运用核心区域图解法和判别分析方法,也初步对泥石流、冰碛和河湖沉积物的粒度特征参数进行了对比研究,建立了判别上述3种沉积物的数学模型(表3)。该数学模型可以看作对萨胡公式的一种补充。
本文将前述所得的各类粒度参数分别代入以上两种公式中,其中萨胡公式选取浅海与河流(三角洲)、河流(三角洲)与浊流判别公式,泥石流、冰碛和河湖相判别公式选取泥石流与河湖相、冰碛与河湖相判别公式。表4为依据上述鉴别公式依次使用矩阵法与直接计算法所得的沉积环境计算结果对比表。

表2 鉴别沉积环境的萨胡判别公式(Sahu,1965)Table 2 The Sahu formula identifying the sedimentary environment (Sahu,1965)
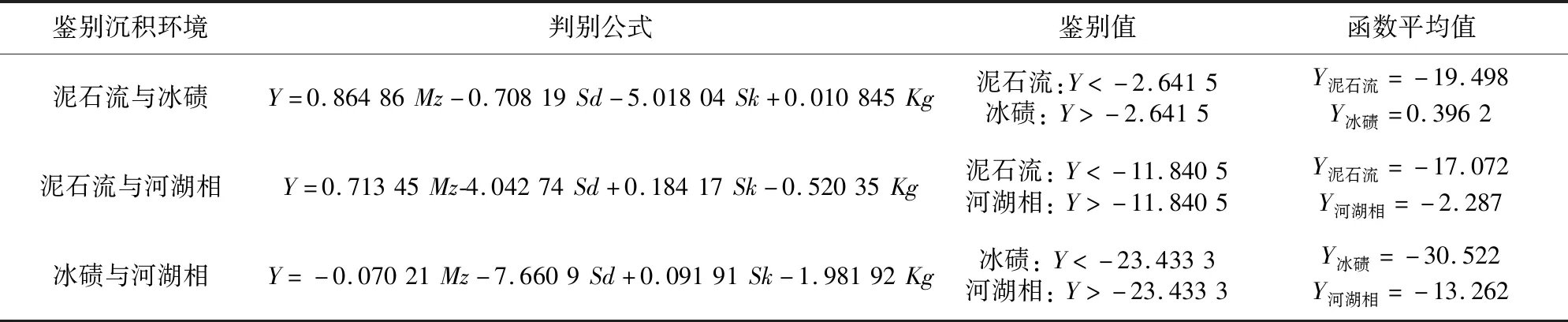
表3 泥石流、冰碛和河湖相沉积判别公式(李昌志等,1999)Table 3 Discrimination formula for deposits of debris flow,moraine and river lake (Li Changzhi et al.,1999)

表4 沉积环境计算结果对比表Table 4 Comparison of calculation results of sedimentary environment
计算结果表明,矩阵法及直接计算法所得结果均判断该碎屑岩来自于河流相环境,与引言中依据所采样品地质背景判断沉积环境为浅湖相及河湖交互相保持一致。矩阵法及直接计算法所得结果除判断河流与浊流环境数值偏差较大外,其余3类环境判断结果较为相近,侧面印证了Mc Manus所提出的矩阵法计算粒度参数公式的可行性。
3 结论
(1) 利用MATLAB图像处理技术,计算机较好地识别了碎屑岩中颗粒轮廓,获取了碎屑岩中所有颗粒的各类形态学参数信息。处理后的碎屑岩图像中,各颗粒轮廓清晰,变形较小,与原镜下照片中轮廓基本保持一致,很好地还原了颗粒及胶结物的原始面貌,大大提高了碎屑岩中颗粒形态学参数的定量化计算程度。
(2) 该方法提高了碎屑岩粒度参数的计算精度。利用MATLAB的统计计算能力,使所有颗粒均参与计算,取代传统粒度参数计算过程中选取少量数据进行统计计算,计算结果更为精确,为判别碎屑岩沉积环境提供了定量参数。在工作中,颗粒标注、统计计算等工作都由计算机完成,减少了大量的工作量,大幅度提高了碎屑岩粒度分析效率。
(3) 该方法在颗粒粒径较大的碎屑岩粒度分析中适用性较好,但对于颗粒粒径较小的细碎屑岩,受制于偏光显微镜分辨率及计算机识别能力,无法区分出颗粒粒径小于15 μm的泥粒与胶结物,存在一定局限性。
