牛初乳粉片混合工艺的优化研究
2020-08-06王青云李凯锋杨晓波
文/王青云 李凯锋 杨晓波
(黑龙江省完达山乳业股份有限公司)
牛初乳粉片是以牛初乳粉为主要原料的一款片剂产品,其生产过程中采用了混合制片工艺。从质量角度看,各种原辅料是否混合均匀,是影响产品质量的关键因素。本品的混合工艺属于粉粒体混合,是干法混合的一种,就是把2 种或2 种以上不同成分组成的粉粒体,依靠外加的适当操作,尽量使各成分的浓度分布达到均匀化的一种操作[1]。评价混合工艺参数是否适宜的比较重要指标是混合均匀度。在实际生产中,混合工艺参数是否合理不仅决定着产品的质量,而且也影响着生产效率。本研究采用干法混合产品原辅料,应用响应面试验优化混合工艺参数,为提高产品质量和实际生产效率提供可靠的依据。
1 材料和方法
1.1 试验材料
按牛初乳粉片产品配方准备试验原料,包括牛初乳粉、白砂糖、赤藓糖醇和香精。
1.2 设备
粉碎机;筛网(20目、80目);SVJ-5L三维混合机;高效液相色谱仪(带紫外检测器和梯度洗脱装置)。
1.3 试验方法
1.3.1 取样
用取样器在混合机上、中、下3 个方位各取3 个样,共9 个样品。取样时不允许有任何翻动或再混合[2]。
1.3.2 混合均匀度评价方法
以同一批次试样中免疫球蛋白IgG含量的相对标准偏差来反映所测产品的混合均匀度[3]:

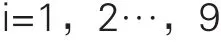

式中,xi为第i样品的免疫球蛋白IgG含量,即第i样品免疫球蛋白IgG含量2 次测定值的算术平均值;xm为所有样品免疫球蛋白IgG含量的算术平均值;RSD为样品免疫球蛋白IgG含量的相对标准偏差;Mh为混合均匀度。
1.3.3 免疫球蛋白IgG含量的测定
参照《GB/T 5009.194—2003 保健食品中免疫球蛋白IgG的测定》。
1.3.4 单因素试验
(1)配料添加方法对混合均匀度的影响
考察不同含量、不同比重物料组分的添加顺序及微量配料预混对混合均匀度的影响。按以下3 种方式进行投料:Ⅰ配料1 次性投入;Ⅱ先加入主料(牛初乳粉、白砂糖和赤藓糖醇),再加入微量配料(香精);Ⅲ先加入大部分主料(牛初乳粉、白砂糖和赤藓糖醇),再加入经预混的微量配料(将香精用3~8 倍重量主料预混)。以装载系数30%计,按配方准确称量各配料,混合20 min后取样,测定免疫球蛋白IgG含量,并计算混合均匀度。
(2)混合时间对混合均匀度的影响
以装载系数30%计,按配方准确称量各配料,采用一次性投料方式,分别在混合5 min、10 min、15 min、20 min、25min时进行取样,测定免疫球蛋白IgG含量,并计算混合均匀度。
(3)装载系数对混合均匀度的影响
按配方准确称量各配料,采用1 次性投料方式,装载系数分别按20%(装载量约1.0 kg)、30%(装载量约1.5 kg)、40%(装载量约2.0 kg)、50%(装载量约2.5kg)、60%(装载量约3.0 kg)5 个水平计,混合20 min后取样,测定免疫球蛋白IgG含量,并计算混合均匀度。
1.3.5 响应面法优化试验设计
首先确定配料的添加按Ⅲ方式处理,在单因素的试验基础上,确定影响混合均匀度的显著因素,采用中心组合试验设计(CCD)模型,选择混合时间(X1)、装载系数(X2)为自变量,以1.414、1、0、-1、-1.414代表自变量水平,以混合均匀度为响应值Y,采用响应面法对混合工艺进行优化。具体试验方案见表1。使用Minitab软件对数据进行分析。

表1 试验因素水平表

图1 配料投料方式对混合均匀度的影响
2 结果与分析
2.1 单因素试验结果分析
2.1.1 配料添加方法对混合均匀度的影响
由试验结果图1可见,配料的投料方法对混合均匀度的影响较大。结果表明,以Ⅲ方式的配料投料方法进行投料,即先加入大部分主料(牛初乳粉、脱盐乳清粉、白砂糖和硬脂酸镁),再加入经预混的微量配料(将香精用3~8 倍重量主料预混),测得混合粉的混合均匀度最高,达到96.42%。
2.1.2 混合时间对混合均匀度的影响
由试验结果图2可知,不同的混合时间对混合均匀度的影响较大。结果表明,当混合时间在5~10 min时,混合粉的混合均匀度为82.53%~90.56%,继续延长混合时间至15 min和20 min时,混合均匀度持续提高,达到95.42%和96.27%,进一步延长混合时间至25 min时,混合均匀度达到95.86%,与15 min和20 min时的混合均匀度无显著差异。结合生产效率因素,把混合时间控制在15 min是比较适宜的。
2.1.3 装载系数对混合均匀度的影响
由试验结果图3可见,不同的装载系数对混合粉的混合均匀度也有较大的影响。在相同的条件下,装载系数20%时,混合粉的混合均匀度仅为90.84%;装载系数30%时,混合均匀度的水平最高,达到96.47%;当装载系数增加到40%时,混合均匀度为96.13%,与装载系数为30%时无显著性差异;但当装载系数超过50%时,混合均匀度明显降低。从结果可以看出,装载系数在30%和40%时,混合粉的混合均匀度是最好的,结合工作效率因素,优选装载系数40%是比较适宜的。

图2 混合时间对混合均匀度的影响
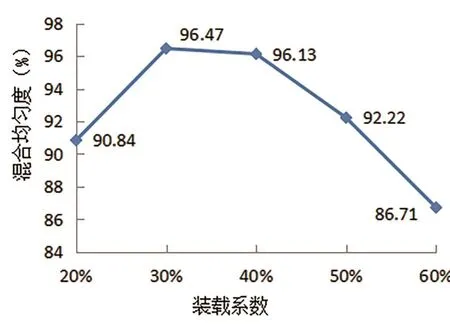
图3 装载系数对混合均匀度的影响
2.2 响应面法优化混合工艺条件
2.2.1 响应面试验方案及结果
根据单因素试验确定的影响混合均匀度的因素和水平,采用CCD试验设计2 因素5 水平的响应面分析试验,以混合均匀度为响应值Y,以混合时间15 min、装载系数40%为中心点实施响应面分析。CCD实验的设计及结果见表2。其中试验1~8是析因试验,试验9~13是中心试验。13 个试验点分为析因和零点,其中析因点为自变量取值在X1、X2所构成的顶点,零点为区域的中心点,零点试验重复5 次,用以估计试验误差。
2.2.2 响应面方差分析
使用Minitab软件对表2的数据进行二次回归分析,回归方差分析结果见表3。经多元回归拟合后,得到以下回归方程(以未编码单位表示):

表3中方差分析结果显示,回归模型P<0.01,差异极显著;模型的拟合优度R2=0.9573,回归模型决定系数R2adj=0.9269,可以用此数学模型解释92.69%的变异性,R2和R2adj比较接近,表明模型与实际情况拟合好。表3中模型失拟项的P值为0.248>0.05,表明模型失拟项不显著,该模型的选择比较合适,而且实验误差小。因此,各因素和响应值之间的真实关系可以由该回归方程来解释,即应用此数学模型进行分析是可行的。
参照表3,模型中一次项X1、X2对混合均匀度的影响均极显著(P<0.01),影响因素按主次顺序排序为:X1>X2;二次项X12、X22对混合均匀度的影响极显著(P<0.01),交互项X1X2无显著交互作用(P>0.05)。
2.2.3 响应面交互作用分析及工艺参数优化
应用Minitab软件绘制响应面图进行三维可视化的分析,结果见图4。等高线的形状可反映出因素之间交互效应的大小,椭圆形表示两因素的交互作用显著,而圆形则表示两因素之间的交互作用不显著。从图4中等高线图可直观的看出混合时间和装载系数交互作用的等高线近似圆形,这表明两者的交互作用不显著。
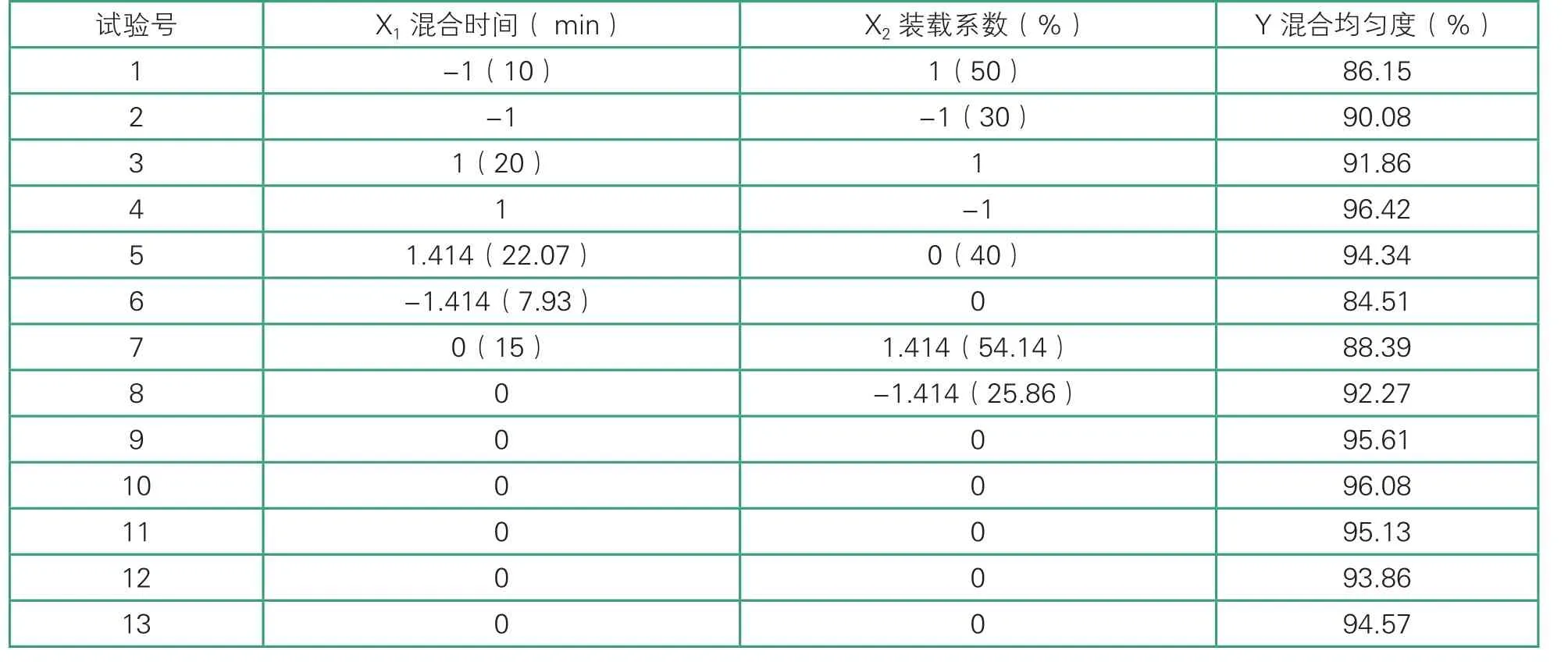
表2 CCD试验设计及结果

表3 CCD设计方差分析结果

图4 混合时间和装载系数交互作用对混合均匀度的影响响应曲面图(左)和等高线图(右)
图4中响应曲面图可以看出,响应值存在最大值,应用Minitab统计分析软件对所建立的数学模型进行最优化分析,可以预测得到模型的最大混合均匀度为96.52%,此时的最优工艺参数分别为:混合时间18.36min,装载系数35.57%。
2.2.4 模型的验证
图5和图6分别为各因素对混合均匀度的交互作用图和影响效应图。由图5可见,混合时间和装载系数两者间交互作用不显著,不同的装载系数条件下,混合均匀度几乎呈相互平行的曲线,可以得出装载系数为35.57%时,其混合均匀度均较其他装载系数条件下的混合均匀度高,结合图6影响效果图可见,混合时间在15~20 min时,混合均匀度均可达到预期效果,结合生产效率因素,把混合时间定为15 min。
对模型求算的最优工艺条件进行验证试验,充分考虑生产过程中便于操作等情况,结合上述的分析,对工艺条件修正为:混合时间15~20 min,装载系数35%。模型验证:以装载系数为35%,混合15 min、18 min和20 min,分别测定混合均匀度,重复进行三次验证试验。结果见表4。
3 个不同混合时间试验条件下的平均混合均匀度分别为94.68%、96.27%和95.27%,结果均符合工艺要求,与模型预测的理论值96.52%均比较接近。因此,采用响应面分析优化得到的牛初乳粉片混合工艺参数具有可行性和可靠性,可用于实际操作。

表4 模型验证试验结果
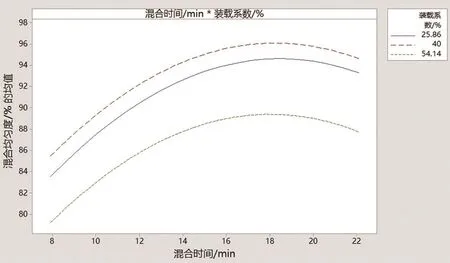
图5 混合均匀度的交互作用图

图6 混合均匀度的影响效应图
3 结论
该牛初乳粉片混合工艺最优参数为:混合15min,装载系数35%。3 个不同混合时间试验条件下的平均混合均匀度分别为94.68%,结果均符合工艺要求,与模型预测的理论值96.52%均比较接近。因此,采用响应面分析优化得到的牛初乳粉片混合工艺参数具有可行性和可靠性,可用于实际操作。
