深海采矿扬矿管的纵向振动分析
2020-08-06肖林京于志豪
肖林京, 左 帅, 于志豪
(山东科技大学机械电子工程学院,青岛 266590)
位于国家管辖海域以外的国际海底区域蕴藏着大量的锰结核[1]。人们利用深海采矿技术,将锰结核从海洋下提取出来。经研究发现,选择管道提升式采矿系统适用于现代化的商业开采[2]。扬矿管在复杂的海洋环境中,在各种力的作用下会使扬矿管产生变形和应力,从而容易引起扬矿管的疲劳破坏和失效,导致使用寿命缩短,严重时还会导致重大的安全事故[3]。因此,对扬矿管纵向振动的研究具有重要的意义。
前人对扬矿系统各部分的子系统进行了研究,并在云南省抚仙湖进行了135 m湖上试验,验证了深海采矿系统的可行性[4]。韩国海洋科学技术院研发了一套KIOST采矿系统,并别在浅水区域和深水区域进行了路径跟踪试验,然后与2015年进行了500 m水深泵和中间矿仓的相关采矿实验[5]。
在理论研究方面,Cui等[6]研究了扬矿管的构型对扬矿管振动和轴向应力的影响;邱显焱[3]对扬矿管的纵向振动进行分析,并采用附加单个吸振器的方法抑制纵向振动;冯雅丽等[7]利用有限元的方法对扬矿管进行了静力分析和动态分析,采用ADINA软件分析了在海水中不同海浪周期下扬矿管的振动特性;梁彬等[8]利用ABAQUS软件进行仿真分析,得到了扬矿管的轴向净身长量,并得到了振动随位置变化的结果。目前,对扬矿管研究主要利用静力学理论对轴向应力和轴向应变进行分析,对于扬矿管的纵向振动分析,忽略了阻尼对固有频率、振动幅值及轴向应力的影响。为此,建立扬矿管的纵向振动微分方程,分别分析在有阻尼系统响应与无阻尼系统响应两种下扬矿管的固有频率、不同点上振幅随时间的变化曲线以及扬矿管顶端轴向应力随时间变化关系。以期为后续对管道稳定性的研究和减振工作提供理论基础。
1 建立扬矿管动力学模型
深海采矿系统的原理图如图1所示,具体工作方式:集矿机(图2)采集多金属结核并进行脱泥和破碎,经软管输送到中间矿仓(图3),再通过泵组经扬矿管输送到采矿船上。

1为采矿船;2为海洋表面;3为泵组;4为扬矿硬管;5为中间矿仓;6为软管;7为集矿机;8为海床图1 深海采矿系统Fig.1 Mining system in the deep sea

图2 中国开展湖试试验中的集矿机Fig.2 China trialed miner in a lake

图3 韩国开展海试试验中的中间矿仓Fig.3 Korea piloted buffer in the sea
扬矿管的总长度为l,上端与采矿船为铰接连接。即扬矿管顶端的运动与采矿船的运动方式相同。扬矿管的末端与软管连接,由于软管的质量和刚度比扬矿管小,因此假设软管不影响扬矿管的振动,末端视为自由端,进一步假设,中间矿仓视为集中质量,现将扬矿管简化为一维振动问题,不考虑扬矿管的偏移、弯矩与扭矩。
扬矿管由无限多质点组成,因此每一截面的位移均不同,扬矿管任意截面x的位移u是关于位置x和时间t的函数,记为u(x,t)。
基于振动力学理论[9]建立扬矿管的纵向振动的偏微分方程[10]。
(1)
式(1)中:A为横截面面积;E为刚度系数。
m(x)=m0+m1δ(x-l)
(2)
式(2)中:δ(x)为狄拉克函数;m0为扬矿管的单位长度质量;m1为中间矿仓集中质量。
c(x)=c0+c1δ(x-l)
(3)
式(3)中:c0为扬矿管单位长度阻尼系数;c1为中间矿仓阻尼系数。
为了求解式(1),需要确定扬矿管的边界条件与初始条件。分析可知,扬矿管的边界条件为上端铰接,下端自由,可以写为
(4)
式(4)中:u0(t)为采矿船的运动,采矿船随着海浪做升沉运动可以看作简谐运动,其简谐运动方程为
u0(t)=rsin(ω0t)
(5)
式(5)中:r为采矿船升沉运动幅值;ω0为运动周期。
扬矿管与采矿船铰接,为采矿船所受到的运动方程。为了求解扬矿管的绝对位移响应u(x,t),可以先求出扬矿管相对于采矿船的相对位移u1(x,t),在通过合成的方法得到u(x,t),表达为
u(x,t)=u1(x,t)+u0(t)
(6)
将式(6)代入扬矿管的纵向振动方程[式(1)]得:
(7)
将式(6)代入扬矿管的边界条件[式(4)]得到扬矿管相对位移的边界条件:
(8)
2 理论分析
2.1 振型函数的分析
扬矿管的纵向振动方程属于波动方程,其求解方法可以用分离变量法来得到,即
u1(x,t)=φ(x)q(t)
(9)
式(9)中:φ(x)为振型函数,是仅与坐标x有关的待定函数;q(t)为时间函数,是仅与时间有关的待定函数,振型函数[11]的通解为
(10)
分别对扬矿管的无阻尼系统响应时的固有频率和有阻尼系统响应时的固有频率进行求解,求解结果如表1所示。

表1 两种情况下固有频率及阻尼比Table 1 Natural frequencies in two conditions and damping ratios
在结合归一化条件,可以求得扬矿管的振型函数为
(11)
采用MATLAB对扬矿管的前5阶振型函数进行绘制,结果如图4所示。

图4 扬矿管的前5阶正则振型函数曲线Fig.4 The first five phases of the regular vibration mode function
2.2 扬矿管振动响应函数的分析
在2.1节已得到扬矿管前5阶的固有频率与相应的振型函数,利用振动型叠加原理对扬矿管的相对位移进行求解,可假设为
(12)
式(12)中:φi(x)为相应于固有频率ωni的主振型;ηi(t)为第i个正则坐标下的响应。将式(12)代入式(7)中得到
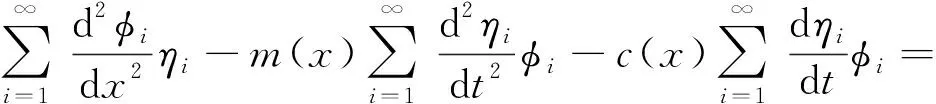
(13)
两边同时乘以φj(x),并沿扬矿管的长度进行积分,得到:
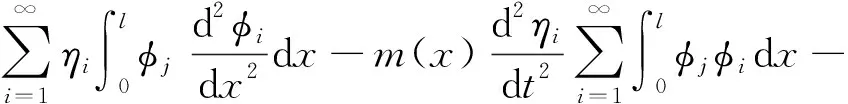
(14)
式(14)中:φi(x)为相应于固有频率ωnj的主振型。
根据正交条件,得到:
(15)
式(15)中:ηj(t)为第j个正则坐标下的响应;ξj为阻尼比,j=1,2,…,n;ωnj为扬矿管的第j阶固有频率,j=1,2,…,n。
(16)
式(17)利用Duhamel积分得到ηj的解:
ηj(t)=ηj(t0)e-ξjωnjtcos(ωdt)+
(17)
式(17)中:ξj为阻尼比;ωd为扬矿系统有阻尼时的固有频率。前5阶阻尼比及扬矿管有阻尼时的前5阶固有频率如表1所示。
根据初始条件:
(18)
将式(11)、式(17)代入式(12)中,再将式(12)、式(5)代入式(6)中,最终可以得到扬矿管随纵向振动方程的解析解。
由扬矿管的响应解可以看出,扬矿管的高阶响应要比扬矿管的低阶响应小,因此计算前5阶响应就可以得到精度较高的结果。
2.3 轴向应力分析
对扬矿系统产生的轴向应力进行分析,其表达式可用式(19)表示。
(19)
式(19)中:Wb为中间矿仓的质量;W0为扬矿管单位长度的质量。
3 仿真分析
利用扬矿管的边界条件最终得到扬矿管的固有频率和有阻尼系统的固有频率,表1为MATLAB[12]计算结果。
利用莫尔在1968、1970年发表的模型试验资料[3]来估的升沉运动幅值,根据莫尔经验公式可得三一垂荡幅值,可以求得r。在六级风况下,采矿船的幅值r=4 m,周期T=10 s[1]。
根据上述计算原则,参考文献[1]中所采用的相关数据,扬矿管的设计参数如表2所示。

表2 扬矿子系统的主要物理参数Table 2 Main physical parameters of the lifting pipe
3.1 无阻尼系统响应时扬矿管的分析
对取样点进行仿真,在不考虑阻尼系统响应的情况下,分别取扬矿管距海平面的1 000、3 000、5 000 m处,研究位移随时间的变化关系。
通过图5可知,在无阻尼系统响应时,从0~1 000 m时振幅变化的最快,3 000 m后的幅值变化较小。在1 000 m内,由于扬矿管相对位移的影响较小,运动规律类似于简谐运动,但随着深度的增加,扬矿管的相对位移振幅的增加。绝对位移变大,在达到峰值的时刻出现许多尖点,容易对扬矿管产生破坏。
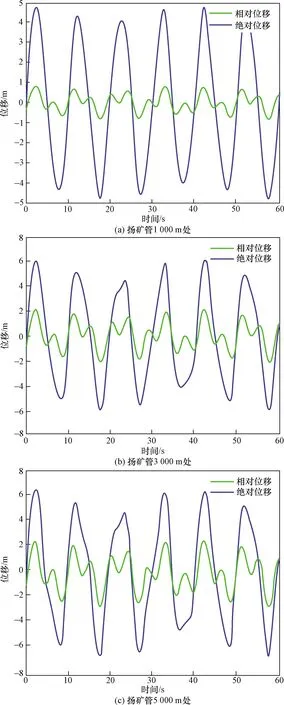
图5 扬矿管1 000、3 000、5 000 m处位移随时间的变化规律(无阻尼)Fig.5 The displacement variation rule of the lifting pipe at 1 000、3 000、5 000 m below sea level with time varying(without damping)
3.2 有阻尼系统响应时扬矿管的分析
在考虑阻尼系统响应的情况下,同样分别取扬矿管距海平面的1 000、3 000、5 000 m处,研究位移随时间的变化关系。
由图6可知,振幅的变化趋势与无阻尼时的振幅变化趋势基本相同。但由于海水阻尼的影响,扬矿管上各点的幅值先减小,后保持稳定的状态。还可以发现,当达到稳态时,扬矿管上任何位置的最大幅值基本稳定5.34 m左右,其运动规律类似于简谐运动。
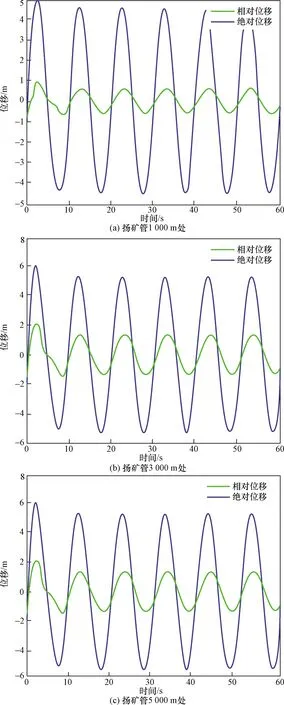
图6 扬矿管1 000、3 000、5 000 m处位移随时间的变化规律(有阻尼)Fig.6 The displacement variation rule of the lifting pipe at 1 000、3 000、5 000 m below sea level with time varying(with damping)
3.3 扬矿管的轴向应力分析
扬矿管所受的轴向应力是影响扬矿管变形的重要因素。下面取扬矿管最顶端的位置,研究轴向应力随时间变化的关系,结果如图7所示。

图7 有无阻尼响应时扬矿管顶端轴向应力随时间变化Fig.7 With and without any damp system responses,axial stress,at the top of the lifting pipe,changes with time
由图7可以看出,当达到稳态时,在有阻尼系统响应要比无阻尼系统更加稳定。且有阻尼系统响应时扬矿管顶端的最大轴向应力要比无阻尼系统响应时的最大轴向应力小25.5%。
在以上两种情况下,在前10 s扬矿管顶端轴向力的变化规律都是先增加后减小,选定前10 s,绘制扬矿管轴向应力随扬矿管位置的变化关系。
由图8可以看出,在大部分时刻,扬矿管的轴向应力随着管长的增加而减小,在个别的时刻会先增大,从1 000 m后在减小。因此,在大部分时刻,扬矿管所受到最大轴向力出现在最顶端。

图8 前10 s轴向应力随位置的变化曲线Fig.8 Axial stress changes with water depth for the 10 s
4 结论
研究了深海采矿扬矿管的纵向振动,建立了扬矿管的纵向振动偏微分方程,求解了扬矿管的振型函数以及响应函数,采用振型叠加法求解了扬矿管的纵向振动公式,并对扬矿管的轴向应力进行分析,得到了如下结论。
(1)在有阻尼系统响应和无阻尼系统响应两种情况下,随着水深的增加,扬矿管上个点的幅值先增大,后逐渐趋于稳定状态。在扬矿管的最末端,前一种情况的最大幅值要比后一种减少1.101 m。
(2)当达到稳态时,有阻尼系统响应条件下的轴向应力的最大值为2.19×108Pa,无阻尼系统响应条件下的轴向应力最大值为1.63×108Pa,减少幅度约为25.5%,且大部分时刻轴向力随着管长增加而减少,少数时刻随着管长的增加,轴向力先增大后减小。
(3)当考虑海水的阻尼时,扬矿管不同点处位移随时间运动规律及轴向应力随时间的变化关系更加规则。因此,海水阻尼可以减少扬矿管突然受到的冲击,使得扬矿管的运动类似简谐运动。
(4)由以上结论可知,扬矿管的最大振幅发生在最下端,在大部分时刻,扬矿管最顶端的轴向应力最大。为此,该研究可以为下一步的减振研究与稳定性研究提供理论依据。在进行减振研究时,可主要在管道的最顶端与最低端展开减振研究工作。
